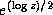Common Lisp the Language, 2nd Edition




Next: Trigonometric and Related
Up: Irrational and Transcendental
Previous: Irrational and Transcendental
Along with the usual one-argument and two-argument exponential and
logarithm functions, sqrt is considered to be an exponential
function, because it raises a number to the power 1/2.
[Function]
exp number
Returns e raised to the power number,
where e is the base of the natural logarithms.
[Function]
expt base-number power-number
Returns base-number raised to the power power-number.
If the base-number is of type rational and the power-number is
an integer,
the calculation will be exact and the result will be of type rational;
otherwise a floating-point approximation may result.

X3J13 voted in March 1989
(COMPLEX-RATIONAL-RESULT)
to clarify that provisions similar to those of the previous paragraph apply to complex
numbers. If the base-number is of type (complex rational)
and the power-number is
an integer,
the calculation will also be exact and the result will be of type
(or rational (complex rational));
otherwise a floating-point or complex floating-point approximation may result.

When power-number is 0 (a zero of type integer),
then the result is always the value 1 in the type of base-number,
even if the base-number is zero (of any type). That is:
(expt x 0) == (coerce 1 (type-of x))
If the power-number is a zero of any other data type,
then the result is also the value 1, in the type of the arguments
after the application of the contagion rules, with one exception:
it is an error if base-number is zero when the power-number
is a zero not of type integer.
Implementations of expt are permitted to use different algorithms
for the cases of a rational power-number and a floating-point
power-number; the motivation is that in many cases greater accuracy
can be achieved for the case of a rational power-number.
For example, (expt pi 16) and (expt pi 16.0) may yield
slightly different results if the first case is computed by repeated squaring
and the second by the use of logarithms. Similarly, an implementation
might choose to compute (expt x 3/2) as if it had
been written (sqrt (expt x 3)), perhaps producing a more accurate
result than would (expt x 1.5). It is left to the implementor
to determine the best strategies.

X3J13 voted in January 1989
(EXPT-RATIO)
to clarify that the preceding remark is in
error, because (sqrt (expt x 3)) does not produce the same value
as (expt x 3/2) in most cases, and to specify that the
specification of the principal value of expt as given in section 12.5.3
should be regarded as definitive.
As an example of the difficulty, let
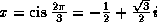 .
Then
.
Then 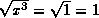 , but
, but
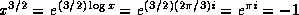 .
Another example is x=-1; then
.
Another example is x=-1; then 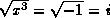 , but
, but
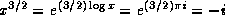 .
.

The result of expt can be a complex number, even when neither argument
is complex, if base-number is negative and power-number
is not an integer. The result is always the principal complex value.
Note that (expt -8 1/3) is not permitted to return -2;
while -2 is indeed one of the cube roots of -8, it is
not the principal cube root, which is a complex number
approximately equal to #C(1.0 1.73205).

Notice of correction. The first edition gave the incorrect value
#C(0.5 1.73205) for the principal cube root of -8. The correct
value is #C(1.0 1.73205), that is, 1+SQRT(3)i. I simply don't know what
I was thinking of!

[Function]
log number &optional base
Returns the logarithm of number in the base base,
which defaults to e, the base of the natural logarithms.
For example:
(log 8.0 2) => 3.0
(log 100.0 10) => 2.0
The result of (log 8 2) may be either 3 or 3.0, depending on the
implementation.
Note that log may return a complex result when given a non-complex
argument if the argument is negative. For example:
(log -1.0) == (complex 0.0 (float pi 0.0))

X3J13 voted in January 1989
(IEEE-ATAN-BRANCH-CUT)
to specify certain floating-point behavior when minus zero is supported.
As a part of that vote it approved a mathematical definition of complex logarithm
in terms of real logarithm, absolute value,
arc tangent of two real arguments, and the phase function as
Logarithm log|z| + i phase z
This specifies the branch cuts precisely whether minus zero is supported or not;
see phase and atan.

[Function]
sqrt number
Returns the principal square root of number.
If the number is not complex but is negative, then the result
will be a complex number.
For example:
(sqrt 9.0) => 3.0
(sqrt -9.0) => #c(0.0 3.0)
The result of (sqrt 9) may be either 3 or 3.0, depending on the
implementation. The result of (sqrt -9) may be either #c(0 3)
or #c(0.0 3.0).

X3J13 voted in January 1989
(IEEE-ATAN-BRANCH-CUT)
to specify certain floating-point behavior when minus zero is supported.
As a part of that vote it approved a mathematical definition of complex square root
in terms of complex logarithm and exponential functions as
Square root 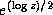
This specifies the branch cuts precisely whether minus zero is supported or not;
see phase and atan.

[Function]
isqrt integer
Integer square root: the argument must be a non-negative integer, and the
result is the greatest integer less than or equal to the exact positive
square root of the argument.
For example:
(isqrt 9) => 3
(isqrt 12) => 3
(isqrt 300) => 17
(isqrt 325) => 18




Next: Trigonometric and Related
Up: Irrational and Transcendental
Previous: Irrational and Transcendental
[email protected]


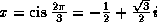 .
Then
.
Then 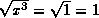 , but
, but
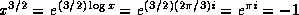 .
Another example is x=-1; then
.
Another example is x=-1; then 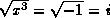 , but
, but
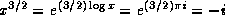 .
.