Contents (GIF version) | Contents (Symbol Font version) | Home © P.D. Terry
8 GRAMMARS AND THEIR CLASSIFICATION
In this chapter we shall explore the underlying ideas behind grammars further, identify some potential problem
areas in designing grammars, and examine the ways in which grammars can be classified. Designing a grammar
to describe the syntax of a programming language is not merely an interesting academic exercise. The effort is, in
practice, usually made so as to be able to aid the development of a translator for the language (and, of course so
that programmers who use the language may have a reference to consult when All Else Fails and they have to
Read The Instructions). Our study thus serves as a prelude to the next chapter, where we shall address the
important problem of parsing rather more systematically than we have done until now.
8.1 Equivalent grammars
As we shall see, not all grammars are suitable as the starting point for developing practical parsing algorithms,
and an important part of compiler theory is concerned with the ability to find equivalent grammars. Two
grammars are said to be equivalent if they describe the same language, that is, can generate exactly the same set of
sentences (not necessarily using the same set of sentential forms or parse trees).
In general we may be able to find several equivalent grammars for any language. A distinct problem in this
regard is a tendency to introduce far too few non-terminals, or alternatively, far too many. It should not have
escaped attention that the names chosen for non-terminals usually convey some semantic implication to the reader,
and the way in which productions are written (that is, the way in which the grammar is factorized) often serves to
emphasize this still further. Choosing too few non-terminals means that semantic implications are very awkward
to discern at all, too many means that one runs the risk of ambiguity, and of hiding the semantic implications in a
mass of hard to follow alternatives.
It may be of some interest to give an approximate count of the numbers of non-terminals and productions that
have been used in the definition of a few languages:
Language Non-terminals Productions
Pascal (Jensen + Wirth report) 110 180
Pascal (ISO standard) 160 300
Edison 45 90
C 75 220
C++ 110 270
ADA 180 320
Modula-2 (Wirth) 74 135
Modula-2 (ISO standard) 225 306
8.2 Case study - equivalent grammars for describing expressions
One problem with the grammars found in text books is that, like many complete programs found in text books,
their final presentation often hides the thought which has gone into their development. To try to redress the
balance, let us look at a typical language construct - arithmetic expressions - and explore several grammars which
seem to define them.
Consider the following EBNF descriptions of simple algebraic expressions. One set is left-recursive, while the
other is right-recursive:
(E1) Goal = Expression . (1)
Expression = Term | Term "-" Expression . (2 ,3)
Term = Factor | Factor "*" Term . (4, 5)
Factor = "a" | "b" | "c" . (6, 7, 8)
(E2) Goal = Expression . (1)
Expression = Term | Expression "-" Term . (2, 3)
Term = Factor | Term "*" Factor . (4, 5)
Factor = "a" | "b" | "c" . (6, 7, 8)
Either of these grammars can be used to derive the string a - b * c, and we show the corresponding phrase
structure trees in Figure 8.1 below.
(E1) Goal (E2) Goal
| |
Expression Expression
| |
.---------+---------------. .---------+------------.
| | | | | |
Term | Expression Expression | Term
| | | | | |
| | Term | | |
| | .-------+-------. | | .-----+-----.
| | | | | | | | | |
| | Factor | Term Term | Term | Factor
| | | | | | | | | |
Factor | | | Factor Factor | Factor | |
| | | | | | | | | |
a - b * c a - b * c
Figure 8.1 Parse trees for the expression a - b * c arising from two grammars
We have already commented that it is frequently the case that the semantic structure of a sentence is reflected in
its syntactic structure, and that this is a very useful property for programming language specification. The
terminals - and * fairly obviously have the "meaning" of subtraction and multiplication. We can reflect this by
drawing the abstract syntax tree (AST) equivalents of the above diagrams; ones constructed essentially by eliding
out the names of the non-terminals, as depicted in Figure 8.2. Both grammars lead to the same AST, of course.
(E1) (E2)
| |
.------ - ---------. .------ - ---------.
| | | |
| .---- * ----. | .---- * ----.
| | | | | |
| | | | | |
| | | | | |
a b c a b c
Figure 8.2 Abstract syntax trees for the expression a - b * c
The appropriate meaning can then be extracted from such a tree by performing a post-order (LRN) tree walk.
While the two sets of productions lead to the same sentences, the second set of productions corresponds to the
usual implied semantics of "left to right" associativity of the operators - and *, while the first set has the awkward
implied semantics of "right to left" associativity. We can see this by considering the parse trees for each grammar
for the string a - b - c, depicted in Figure 8.3.
(E1) Goal (E2) Goal
| |
Expression Expression
| |
.---------+---------------. .---------------+------.
| | | | | |
Term | Expression Expression | Term
| | | | | |
| | .-------+-------. .-------+-------. | |
| | | | | | | | | |
| | Term | Expression Expression | Term | Factor
| | | | | | | | | |
| | Factor | Term Term | Factor | |
| | | | | | | | | |
Factor | | | Factor Factor | | | |
| | | | | | | | | |
a - b - c a - b - c
Figure 8.3 Parse trees for the expression a - b - c arising from two grammars
Another attempt at writing a grammar for this language is of interest:
(E3) Goal = Expression . (1)
Expression = Term | Term "*" Expression . (2, 3)
Term = Factor | Factor "-" Term . (4, 5)
Factor = "a" | "b" | "c" . (6, 7, 8)
Here we have the unfortunate situation that not only is the associativity of the operators wrong; the relative
precedence of multiplication and subtraction has also been inverted from the norm. This can be seen from the
parse tree for the expression a - b * c shown in Figure 8.4.
(E3) Goal
|
Expression
|
.------------------+------------.
| | |
Term | Expression
| | |
.---------+---------. | |
| | | | Term
Factor | Term | |
| | | | |
| | Factor | Factor
| | | | |
a - b * c
Figure 8.4 Parse tree for the expression a - b * c arising from grammar E3
Of course, if we use the EBNF metasymbols it is possible to write grammars without using recursive productions.
Two such grammars follow:
(E4) Goal = Expression . (1)
Expression = Term { "-" Term } . (2)
Term = Factor { "*" Factor } . (3)
Factor = "a" | "b" | "c" . (4, 5, 6)
(E5) Goal = Expression . (1)
Expression = { Term "-" } Term . (2)
Term = { Factor "*" } Factor . (3)
Factor = "a" | "b" | "c" . (4, 5, 6)
Exercises
8.1 Draw syntax diagrams which reflect the different approaches taken to factorizing these grammars.
8.2 Comment on the associativity and precedence that seem to underpin grammars E4 and E5.
8.3 Develop sets of productions for algebraic expressions that will describe the operations of addition and
division as well as subtraction and multiplication. Analyse your attempts in some detail, paying heed to
the issues of associativity and precedence.
8.4 Develop sets of productions which describe expressions exemplified by
- a + sin(b + c) * ( - ( b - a) )
that is to say, fairly general mathematical expressions, with bracketing, leading unary signs, the usual
operations of addition, subtraction, division and multiplication, and simple function calls. Ensure that
the productions correspond to the conventional precedence and associativity rules for arithmetic
expressions.
8.5 Extend Exercise 8.4 to allow for exponentiation as well.
8.3 Some simple restrictions on grammars
Had he looked at our grammars, Mr. Orwell might have been tempted to declare that, while they might be equal,
some are more equal than others. Even with only limited experience we have seen that some grammars will have
features which will make them awkward to use as the basis of compiler development. There are several standard
restrictions which are called for by different parsing techniques, among which are some fairly obvious ones.
8.3.1 Useless productions and reduced grammars
For a grammar to be of practical value, especially in the automatic construction of parsers and compilers, it
should not contain superfluous rules that cannot be used in parsing a sentence. Detection of useless productions
may seem a waste of time, but it may also point to a clerical error (perhaps an omission) in writing the
productions. An example of a grammar with useless productions is
G = { N , T , S , P }
N = { W , X , Y , Z }
T = { a }
S = W
P =
W  aW (1)
W
aW (1)
W  Z (2)
W
Z (2)
W  X (3)
Z
X (3)
Z  aZ (4)
X
aZ (4)
X  a (5)
Y
a (5)
Y  aa (6)
aa (6)
The useful productions are (1), (3) and (5). Production (6) ( Y  aa ) is useless, because Y is non-reachable
or non-derivable - there is no way of introducing Y into a sentential form (that is, S
aa ) is useless, because Y is non-reachable
or non-derivable - there is no way of introducing Y into a sentential form (that is, S 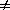 >*
>*  Y
Y for any
for any  ,
,  ).
Productions (2) and (4) are useless, because Z is non-terminating - if Z appears in a sentential form then this
cannot generate a terminal string (that is, Z
).
Productions (2) and (4) are useless, because Z is non-terminating - if Z appears in a sentential form then this
cannot generate a terminal string (that is, Z 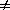 >*
>*  for any
for any 
 T *).
T *).
A reduced grammar is one that does not contain superfluous rules of these two types (non-terminals that can
never be reached from the start symbol, and non-terminals that cannot produce terminal strings).
More formally, a context-free grammar is said to be reduced if, for each non-terminal B we can write
S 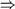 *
*  B
B 
for some strings  and
and  , and where
, and where
B 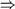 *
* 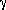
for some 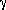
 T * .
T * .
In fact, non-terminals that cannot be reached in any derivation from the start symbol are sometimes added so as to
assist in describing the language - an example might be to write, for C
Comment = "/*" CommentString "*/" .
CommentString = character | CommentString character .
8.3.2  -free grammars
-free grammars
Intuitively we might expect that detecting the presence of "nothing" would be a little awkward, and for this reason
certain compiling techniques require that a grammar should contain no  -productions (those which generate the
null string). Such a grammar is referred to as an
-productions (those which generate the
null string). Such a grammar is referred to as an  -free grammar.
-free grammar.
 -productions are usually used in BNF as a way of terminating recursion, and are often easily removed. For
example, the productions
-productions are usually used in BNF as a way of terminating recursion, and are often easily removed. For
example, the productions
Integer = digit RestOfInteger .
RestOfInteger = digit RestOfInteger |  .
digit = "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" .
.
digit = "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" .
can be replaced by the  -free equivalent
-free equivalent
Integer = digit | Integer digit .
digit = "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" .
Such replacement may not always be so easy: the reader might like to look at the grammar of Section 8.7, which
uses  -productions to express ConstDeclarations, VarDeclarations and Statement, and try to eliminate them.
-productions to express ConstDeclarations, VarDeclarations and Statement, and try to eliminate them.
8.3.3 Cycle-free grammars
A production in which the right side consists of a single non-terminal
A  B ( where A , B
B ( where A , B  N )
N )
is termed a single production. Fairly obviously, a single production of the form
A  A
A
serves no useful purpose, and should never be present. It could be argued that it causes no harm, for it
presumably would be an alternative which was never used (so being useless, in a sense not quite that discussed
above). A less obvious example is provided by the set of productions
A  B
B
B  C
C
C  A
A
Not only is this useless in this new sense, it is highly undesirable from the point of obtaining a unique parse, and
so all parsing techniques require a grammar to be cycle-free - it should not permit a derivation of the form
A 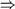 + A
+ A
8.4 Ambiguous grammars
An important property which one looks for in programming languages is that every sentence that can be generated
by the language should have a unique parse tree, or, equivalently, a unique left (or right) canonical parse. If a
sentence produced by a grammar has two or more parse trees then the grammar is said to be ambiguous. An
example of ambiguity is provided by another attempt at writing a grammar for simple algebraic expressions - this
time apparently simpler than before:
(E6) Goal = Expression . (1)
Expression = Expression "-" Expression (2)
| Expression "*" Expression (3)
| Factor . (4)
Factor = "a" | "b" | "c" . (5, 6, 7)
With this grammar the sentence a - b * c has two distinct parse trees and two canonical derivations. We refer to
the numbers to show the derivation steps.
(E6) Goal
|
Expression
|
.------------+------------------.
| | |
Expression | Expression
| | .---------+--------.
| | | | |
Factor | Expression | Expression
| | | | |
| | Factor | Factor
| | | | |
a - b * c
Figure 8.5 One parse tree for the expression a - b * c using grammar E6
The parse tree shown in Figure 8.5 corresponds to the derivation
Goal  Expression (1)
Expression (1)
 Expression - Expression (2)
Expression - Expression (2)
 Factor - Expression (4)
Factor - Expression (4)
 a - Expression (5)
a - Expression (5)
 a - Expression * Expression (3)
a - Expression * Expression (3)
 a - Factor * Expression (4)
a - Factor * Expression (4)
 a - b * Expression (6)
a - b * Expression (6)
 a - b * Factor (4)
a - b * Factor (4)
 a - b * c (7)
a - b * c (7)
while the second derivation
Goal  Expression (1)
Expression (1)
 Expression * Expression (3)
Expression * Expression (3)
 Expression - Expression * Expression (2)
Expression - Expression * Expression (2)
 Factor - Expression * Expression (4)
Factor - Expression * Expression (4)
 a - Expression * Expression (5)
a - Expression * Expression (5)
 a - Factor * Expression (4)
a - Factor * Expression (4)
 a - b * Expression (6)
a - b * Expression (6)
 a - b * Factor (4)
a - b * Factor (4)
 a - b * c (7)
a - b * c (7)
corresponds to the parse tree depicted in Figure 8.6.
(E6) Goal
|
Expression
|
.-----------------+------------.
| | |
Expression | Expression
| | |
.-------+-------. | |
| | | | |
Expression | Expression | Factor
| | | | |
Factor | Factor | |
| | | | |
a - b * c
Figure 8.6 Another parse tree for the expression a - b * c using grammar E6
If the only use for grammars was to determine whether a string belonged to the language, ambiguity would be of
little consequence. However, if the meaning of a program is to be tied to its syntactic structure, then ambiguity
must be avoided. In the example above, the two trees correspond to two different evaluation sequences for the
operators * and - . In the first case the "meaning" would be the usual mathematical one, namely a - (b * c),
but in the second case the meaning would effectively be (a - b) * c .
We have already seen various examples of unambiguous grammars for this language in an earlier section, and in
this case, fortunately, ambiguity is quite easily avoided.
The most famous example of an ambiguous grammar probably relates to the IF ... THEN ... ELSE statement in
simple Algol-like languages. Let us demonstrate this by defining a simple grammar for such a construct.
Program = Statement .
Statement = Assignment | IfStatement .
Assignment = Variable ":=" Expression .
Expression = Variable .
Variable = "i" | "j" | "k" | "a" | "b" | "c" .
IfStatement = "IF" Condition "THEN" Statement
| "IF" Condition "THEN" Statement "ELSE" Statement .
Condition = Expression "=" Expression
| Expression "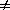 " Expression .
" Expression .
In this grammar the string
IF i = j THEN IF i = k THEN a := b ELSE a := c
has two possible parse trees. The reader is invited to draw these out as an exercise; the essential point is that we
can parse the string to correspond either to
IF i = j THEN (IF i = k THEN a := b ELSE a := c)
ELSE (nothing)
or to
IF i = j THEN (IF i = k THEN a := b ELSE nothing)
ELSE (a := c)
Any language which allows a sentence such as this may be inherently ambiguous unless certain restrictions are
imposed on it, for example, on the part following the THEN of an IfStatement, as was done in Algol (Naur, 1963).
In Pascal and C++, as is hopefully well known, an ELSE is deemed to be attached to the most recent unmatched
THEN, and the problem is avoided that way. In other languages it is avoided by introducing closing tokens like
ENDIF and ELSIF. It is, however, possible to write productions that are unambiguous:
Statement = Matched | Unmatched .
Matched = "IF" Condition "THEN" Matched "ELSE" Matched
| OtherStatement .
Unmatched = "IF" Condition "THEN" Statement
| "IF" Condition "THEN" Matched "ELSE" Unmatched .
In the general case, unfortunately, no algorithm exists (or can exist) that can take an arbitrary grammar and
determine with certainty and in a finite amount of time whether it is ambiguous or not. All that one can do is to
develop fairly simple but non-trivial conditions which, if satisfied by a grammar, assure one that it is
unambiguous. Fortunately, ambiguity does not seem to be a problem in practical programming languages.
Exercises
8.6 Convince yourself that the last set of productions for IF ... THEN ... ELSE statements is unambiguous.
8.5 Context sensitivity
Some potential ambiguities belong to a class which is usually termed context-sensitive. Spoken and written
language is full of such examples, which the average person parses with ease, albeit usually within a particular
cultural context or idiom. For example, the sentences
Time flies like an arrow
and
Fruit flies like a banana
in one sense have identical construction
Noun Verb Adverbial phrase
but, unless we were preoccupied with aerodynamics, in listening to them we would probably subconsciously parse
the second along the lines of
Adjective Noun Verb Noun phrase
Examples like this can be found in programming languages too. In Fortran a statement of the form
A = B(J)
(when taken out of context) could imply a reference either to the Jth element of array B, or to the evaluation of a
function B with integer argument J. Mathematically there is little difference - an array can be thought of as a
mapping, just as a function can, although programmers may not often think that way.
8.6 The Chomsky hierarchy
Until now all our practical examples of productions have had a single non-terminal on the left side, although
grammars may be more general than that. Based on pioneering work by a linguist (Chomsky, 1959), computer
scientists now recognize four classes of grammar. The classification depends on the format of the productions,
and may be summarized as follows:
8.6.1 Type 0 Grammars (Unrestricted)
An unrestricted grammar is one in which there are virtually no restrictions on the form of any of the productions,
which have the general form


 with
with 
 (N
(N  T )* N (N
T )* N (N  T )* ,
T )* , 
 (N
(N  T )*
T )*
(thus the only restriction is that there must be at least one non-terminal symbol on the left side of each
production). The other types of grammars are more restricted; to qualify as being of type 0 rather than one of
these more restricted types it is necessary for the grammar to contain at least one production 

 with |
with |  | >
|
| >
|  |, where |
|, where |  | denotes the length of
| denotes the length of  . Such a production can be used to "erase" symbols - for example,
aAB
. Such a production can be used to "erase" symbols - for example,
aAB  aB erases A from the context aAB. This type is so rare in computer applications that we shall consider
it no further here. Practical grammars need to be far more restricted if we are to base translators on them.
aB erases A from the context aAB. This type is so rare in computer applications that we shall consider
it no further here. Practical grammars need to be far more restricted if we are to base translators on them.
8.6.2 Type 1 Grammars (Context-sensitive)
If we impose the restriction on a type 0 grammar that the number of symbols in the string on the left of any
production is less than or equal to the number of symbols on the right side of that production, we get the subset of
grammars known as type 1 or context-sensitive. In fact, to qualify for being of type 1 rather than of a yet more
restricted type, it is necessary for the grammar to contain at least one production with a left side longer than one
symbol.
Productions in type 1 grammars are of the general form


 with |
with |  |
|  |
|  | ,
| , 
 (N
(N  T )* N (N
T )* N (N  T )* ,
T )* , 
 (N
(N  T )+
T )+
Strictly, it follows that the null string would not be allowed as a right side of any production. However, this is
sometimes overlooked, as  -productions are often needed to terminate recursive definitions. Indeed, the exact
definition of "context-sensitive" differs from author to author. In another definition, productions are required to
be limited to the form
-productions are often needed to terminate recursive definitions. Indeed, the exact
definition of "context-sensitive" differs from author to author. In another definition, productions are required to
be limited to the form
 A
A


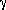
 with
with  ,
, 
 (N
(N  T )*, A
T )*, A  N+,
N+, 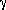
 (N
(N  T )+
T )+
although examples are often given where productions are of a more general form, namely
 A
A

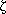
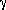
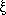 with
with  ,
,  ,
, 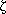 ,
, 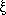
 (N
(N  T )*, A
T )*, A  N+,
N+, 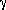
 (N
(N  T )+
T )+
(It can be shown that the two definitions are equivalent.) Here we can see the meaning of context-sensitive more
clearly - A may be replaced by 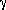 when A is found in the context of (that is, surrounded by)
when A is found in the context of (that is, surrounded by)  and
and  .
.
A much quoted simple example of such a grammar is as follows:
G = { N , T , S , P }
N = { A , B , C }
T = { a , b , c }
S = A
P =
A  aABC | abC (1, 2)
CB
aABC | abC (1, 2)
CB  BC (3)
bB
BC (3)
bB  bb (4)
bC
bb (4)
bC  bc (5)
cC
bc (5)
cC  cc (6)
cc (6)
Let us derive a sentence using this grammar. A is the start string: let us choose to apply production (1)
A  aABC
aABC
and then in this new string choose another production for A, namely (2) to derive
A  a abC BC
a abC BC
and follow this by the use of (3). (We could also have chosen (5) at this point.)
A  aab BC C
aab BC C
We follow this by using (4) to derive
A  aa bb CC
aa bb CC
followed by the use of (5) to get
A  aab bc C
aab bc C
followed finally by the use of (6) to give
A  aabbcc
aabbcc
However, with this grammar it is possible to derive a sentential form to which no further productions can be
applied. For example, after deriving the sentential form
aabCBC
if we were to apply (5) instead of (3) we would obtain
aabcBC
but no further production can be applied to this string. The consequence of such a failure to obtain a terminal
string is simply that we must try other possibilities until we find those that yield terminal strings. The
consequences for the reverse problem, namely parsing, are that we may have to resort to considerable
backtracking to decide whether a string is a sentence in the language.
Exercises
8.7 Derive (or show how to parse) the strings
abc and aaabbbccc
using the above grammar.
8.8 Show informally that the strings
abbc , aabc and abcc
cannot be derived using this grammar.
8.9 Derive a context-sensitive grammar for strings of 0's and 1's so that the number of 0's and 1's is the
same.
8.10 Attempt to write context-sensitive productions from which the English examples in section 8.5 could be
derived.
8.11 An attempt to use context-sensitive productions in an actual computer language was made by Lee (1972),
who gave such productions for the PRINT statement in BASIC. Such a statement may be described
informally as having the keyword PRINT followed by an arbitrary number of Expressions and Strings.
Between each pair of Expressions a Separator is required, but between any other pair (String -
Expression, String - String or Expression - String) the Separator is optional.
Study Lee's work, criticize it, and attempt to describe the BASIC PRINT statement using a context-free
grammar.
8.6.3 Type 2 Grammars (Context-free)
A more restricted subset of context-sensitive grammars yields the type 2 or context-free grammars. A grammar is
context-free if the left side of every production consists of a single non-terminal, and the right side consists of a
non-empty sequence of terminals and non-terminals, so that productions have the form


 with |
with |  |
|  |
|  | ,
| , 
 N ,
N , 
 (N
(N  T )+
T )+
that is
A 
 with A
with A  N ,
N , 
 (N
(N  T )+
T )+
Strictly, as before, no  -productions should be allowed, but this is often relaxed to allow
-productions should be allowed, but this is often relaxed to allow 
 (N
(N  T)*. Such
productions are easily seen to be context-free, because if A occurs in any string, say
T)*. Such
productions are easily seen to be context-free, because if A occurs in any string, say 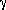 A
A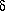 , then we may effect a
derivation step
, then we may effect a
derivation step 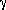 A
A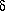
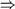
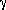

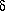 without any regard for the particular context (prefix or suffix) in which A occurs.
without any regard for the particular context (prefix or suffix) in which A occurs.
Most of our earlier examples have been of this form, and we shall consider a larger example shortly, for a
complete small programming language.
Exercises
8.12 Develop a context-free grammar that specifies the set of REAL decimal literals that may be written in
Fortran. Examples of these literals are
-21.5 0.25 3.7E-6 .5E7 6E6 100.0E+3
8.13 Repeat the last exercise for REAL literals in Modula-2 and Pascal, and float literals in C++.
8.14 Find a context-free grammar that describes Modula-2 comments (unlike Pascal and C++, these may be
nested).
8.15 Develop a context-free grammar that generates all palindromes constructed of the letters a and b
(palindromes are strings that read the same from either end, like ababbaba).
8.6.4 Type 3 Grammars (Regular, Right-linear or Left-linear)
Imposing still further constraints on productions leads us to the concept of a type 3 or regular grammar. This can
take one or other of two forms (but not both at once). It is right-linear if the right side of every production
consists of zero or one terminal symbols, optionally followed by a single non-terminal, and if the left side is a
single non-terminal, so that productions have the form
A  a or A
a or A  aB with a
aB with a  T , A, B
T , A, B  N
N
It is left-linear if the right side of every production consists of zero or one terminals optionally preceded by a
single non-terminal, so that productions have the form
A  a or A
a or A  Ba with a
Ba with a  T , A, B
T , A, B  N
N
(Strictly, as before,  productions are ruled out - a restriction often overlooked). A simple example of such a
grammar is one for describing binary integers
productions are ruled out - a restriction often overlooked). A simple example of such a
grammar is one for describing binary integers
BinaryInteger = "0" BinaryInteger | "1" BinaryInteger | "0" | "1" .
Regular grammars are rather restrictive - local features of programming languages like the definitions of integer
numbers and identifiers can be described by them, but not much more. Such grammars have the property that
their sentences may be parsed by so-called finite state automata, and can be alternatively described by regular
expressions, which makes them of theoretical interest from that viewpoint as well.
Exercises
8.16 Can you describe signed integers and Fortran identifiers in terms of regular grammars as well as in terms
of context-free grammars?
8.17 Can you develop a regular grammar that specifies the set of float decimal literals that may be written in
C++?
8.18 Repeat the last exercise for REAL literals in Modula-2, Pascal and Fortran.
8.6.5 The relationship between grammar type and language type
It should be clear from the above that type 3 grammars are a subset of type 2 grammars, which themselves form a
subset of type 1 grammars, which in turn form a subset of type 0 grammars (see Figure 8.7).
.------------------------------------------------------------------.
| .-------------------------------------------------. |
| | .--------------------------------. | |
| | | .--------------. | | |
| | | | Type 3 | Type 2 | Type 1 | Type 0 |
| | | | | | | |
| | | | Regular | Context-free | Context- | Unrestricted |
| | | | | | sensitive | |
| | | `--------------' | | |
| | `--------------------------------' | |
| `-------------------------------------------------' |
`------------------------------------------------------------------'
Figure 8.7 The Chomsky hierarchy of grammars
A language L(G) is said to be of type k if it can be generated by a type k grammar. Thus, for example, a
language is said to be context-free if a context-free grammar may be used to define it. Note that if a non context-
free definition is given for a particular language, it does not necessarily imply that the language is not context-free
- there may be an alternative (possibly yet-to-be-discovered) context-free grammar that describes it. Similarly, the
fact that a language can, for example, most easily be described by a context-free grammar does not necessarily
preclude our being able to find an equivalent regular grammar.
As it happens, grammars for modern programming languages are usually largely context-free, with some
unavoidable context-sensitive features, which are usually handled with a few extra ad hoc rules and by using so-
called attribute grammars, rather than by engaging on the far more difficult task of finding suitable context-
sensitive grammars. Among these features are the following:
- The declaration of a variable must precede its use.
- The number of formal and actual parameters in a procedure call must be the same.
- The number of index expressions or fields in a variable designator must match the number specified in its
declaration.
Exercises
8.19 Develop a grammar for describing scanf or printf statements in C. Can this be done in a context-free
way, or do you need to introduce context-sensitivity?
8.20 Develop a grammar for describing Fortran FORMAT statements. Can this be done in a context-free
way, or do you need to introduce context-sensitivity?
Further reading
The material in this chapter is very standard, and good treatments of it can be found in many books. The keen
reader might do well to look at the alternative presentation in the books by Gough (1988), Watson (1989),
Rechenberg and Mössenböck (1989), Watt (1991), Pittman and Peters (1992), Aho, Sethi and Ullman (1986), or
Tremblay and Sorenson (1985). The last three references are considerably more rigorous than the others, drawing
several fine points which we have glossed over, but are still quite readable.
8.7 Case study - Clang
As a rather larger example, we give here the complete syntactic specification of a simple programming language,
which will be used as the basis for discussion and enlargement at several points in the future. The language is
called Clang, an acronym for Concurrent Language (also chosen because it has a fine ring to it), deliberately
contains a mixture of features drawn from languages like Pascal and C++, and should be immediately
comprehensible to programmers familiar with those languages.
The semantics of Clang, and especially the concurrent aspects of the extensions that give it its name, will be
discussed in later chapters. It will suffice here to comment that the only data structures (for the moment) are the
scalar INTEGER and simple arrays of INTEGER.
8.7.1 BNF Description of Clang
In the first set of productions we have used recursion to show the repetition:
COMPILER Clang
IGNORE CASE
IGNORE CHR(9) .. CHR(13)
COMMENTS FROM "(*" TO "*)"
CHARACTERS
cr = CHR(13) .
lf = CHR(10) .
letter = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz" .
digit = "0123456789" .
instring = ANY - "'" - cr - lf .
TOKENS
identifier = letter { letter | digit } .
number = digit { digit } .
string = "'" (instring | "''") { instring | "''" } "'" .
PRODUCTIONS
Clang = "PROGRAM" identifier ";" Block "." .
Block = Declarations CompoundStatement .
Declarations = OneDeclaration Declarations | .
OneDeclaration = ConstDeclarations | VarDeclarations .
ConstDeclarations = "CONST" ConstSequence .
ConstSequence = OneConst | ConstSequence OneConst .
OneConst = identifier "=" number ";" .
VarDeclarations = "VAR" VarSequence ";" .
VarSequence = OneVar | VarSequence "," OneVar .
OneVar = identifier UpperBound .
UpperBound = "[" number "]" | .
CompoundStatement = "BEGIN" StatementSequence "END" .
StatementSequence = Statement | StatementSequence ";" Statement .
Statement = CompoundStatement | Assignment
| IfStatement | WhileStatement
| ReadStatement | WriteStatement | .
Assignment = Variable ":=" Expression .
Variable = Designator .
Designator = identifier Subscript .
Subscript = "[" Expression "]" | .
IfStatement = "IF" Condition "THEN" Statement .
WhileStatement = "WHILE" Condition "DO" Statement .
Condition = Expression RelOp Expression .
ReadStatement = "READ" "(" VariableSequence ")" .
VariableSequence = Variable | VariableSequence "," Variable .
WriteStatement = "WRITE" WriteParameters .
WriteParameters = "(" WriteSequence ")" | .
WriteSequence = WriteElement | WriteSequence "," WriteElement .
WriteElement = string | Expression .
Expression = Term | AddOp Term | Expression AddOp Term .
Term = Factor | Term MulOp Factor .
Factor = Designator | number | "(" Expression ")" .
AddOp = "+" | "-" .
MulOp = "*" | "/" .
RelOp = "=" | "<>" | "<" | "<=" | ">" | ">=" .
END Clang.
8.7.2 EBNF description of Clang
As usual, an EBNF description is somewhat more concise:
COMPILER Clang
IGNORE CASE
IGNORE CHR(9) .. CHR(13)
COMMENTS FROM "(*" TO "*)"
CHARACTERS
cr = CHR(13) .
lf = CHR(10) .
letter = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz" .
digit = "0123456789" .
instring = ANY - "'" - cr - lf .
TOKENS
identifier = letter { letter | digit } .
number = digit { digit } .
string = "'" (instring | "''") { instring | "''" } "'" .
PRODUCTIONS
Clang = "PROGRAM" identifier ";" Block "." .
Block = { ConstDeclarations | VarDeclarations }
CompoundStatement .
ConstDeclarations = "CONST" OneConst { OneConst } .
OneConst = identifier "=" number ";" .
VarDeclarations = "VAR" OneVar { "," OneVar } ";" .
OneVar = identifier [ UpperBound ] .
UpperBound = "[" number "]" .
CompoundStatement = "BEGIN" Statement { ";" Statement } "END" .
Statement = [ CompoundStatement | Assignment
| IfStatement | WhileStatement
| ReadStatement | WriteStatement ] .
Assignment = Variable ":=" Expression .
Variable = Designator .
Designator = identifier [ "[" Expression "]" ] .
IfStatement = "IF" Condition "THEN" Statement .
WhileStatement = "WHILE" Condition "DO" Statement .
Condition = Expression RelOp Expression .
ReadStatement = "READ" "(" Variable { "," Variable } ")" .
WriteStatement = "WRITE"
[ "(" WriteElement { "," WriteElement } ")" ] .
WriteElement = string | Expression .
Expression = ( "+" Term | "-" Term | Term ) { AddOp Term } .
Term = Factor { MulOp Factor } .
Factor = Designator | number | "(" Expression ")" .
AddOp = "+" | "-" .
MulOp = "*" | "/" .
RelOp = "=" | "<>" | "<" | "<=" | ">" | ">=" .
END Clang.
8.7.3 A sample program
It is fairly common practice to illustrate a programming language description with an example of a program
illustrating many of the language's features. To keep up with tradition, we follow suit. The rather obtuse way in
which Eligible is incremented before being used in a subscripting expression in line 16 is simply to illustrate that
a subscript can be an expression.
PROGRAM Debug;
CONST
VotingAge = 18;
VAR
Eligible, Voters[100], Age, Total;
BEGIN
Total := 0;
Eligible := 0;
READ(Age);
WHILE Age > 0 DO
BEGIN
IF Age > VotingAge THEN
BEGIN
Voters[Eligible] := Age;
Eligible := Eligible + 1;
Total := Total + Voters[Eligible - 1]
END;
READ(Age);
END;
WRITE(Eligible, ' voters. Average age = ', Total / Eligible);
END.
Exercises
8.21 Do the BNF style productions use right or left recursion? Write an equivalent grammar which uses the
opposite form of recursion.
8.22 Develop a set of syntax diagrams for Clang (see section 5.10).
8.23 We have made no attempt to describe the semantics of programs written in Clang; to a reader familiar
with similar languages they should be self-evident. Write simple programs in the language to:
(a) Find the sum of the numbers between two input data, which can be supplied in either order.
(b) Use Euclid's algorithm to find the HCF of two integers.
(c) Determine which of a set of year dates correspond to leap years.
(d) Read a sequence of numbers and print out the embedded monotonic increasing sequence.
(e) Use a "sieve" algorithm to determine which of the numbers less than 255 are prime.
In the light of your experience in preparing these solutions, and from the intuition which you have from
your background in other languages, can you foresee any gross deficiencies in Clang as a language for
handling problems in integer arithmetic (apart from its lack of procedural facilities, which we shall deal
with in a later chapter)?
8.24 Suppose someone came to you with the following draft program, seeking answer to the questions
currently found in the comments next to some statements. How many of these questions can you answer
by referring only to the syntactic description given earlier? (The program is not supposed to do anything
useful!)
PROGRAM Query;
CONST
Header = 'Title'; (* Can I declare a string constant? *)
VAR
L1[10], L2[10], (* Are these the same size? *)
L3[20], I, Query, (* Can I reuse the program name as a variable? *)
L3[15]; (* What happens if I use a variable name again? *)
CONST (* Can I declare constants after variables? *)
Max = 1000;
Min = -89; (* Can I define negative constants? *)
VAR (* Can I have another variable section? *)
BigList[Max]; (* Can I use named constants to set array sizes? *)
BEGIN
Write(Heading) (* Can I write constants? *)
L1[10] := 34; (* Does L[10] exist? *)
L1 := L2; (* Can I copy complete arrays? *)
Write(L3); (* Can I write complete arrays? *)
;; I := Query;;; (* What about spurious semicolons? *)
END.
8.25 As a more challenging exercise, consider a variation on Clang, one that resembles C++ rather more
closely than it does Pascal. Using the translation below of the sample program given earlier as a guide,
derive a grammar that you think describes this language (which we shall later call "Topsy"). For
simplicity, regard cin and cout as keywords leading to special statement forms.
void main (void) {
const VotingAge = 18;
int Eligible, Voters[100], Age, Total;
Total = 0;
Eligible = 0;
cin >> Age;
while (Age > 0) {
if (Age > VotingAge) {
Voters[Eligible] = Age;
Eligible = Eligible + 1;
Total = Total + Voters[Eligible - 1];
}
cin >> Age;
}
cout << Eligible << " voters. Average age = " << Total / Eligible;
}
8.26 In the light of your experience with Exercises 8.24 and 8.25, discuss the ease of "reverse-engineering" a
programming language description by consulting only a few example programs? Why do you suppose so
many students attempt to learn programming by imitation?
8.27 Modify the Clang language definition to incorporate Pascal-like forms of:
(a) the REPEAT ... UNTIL statement
(b) the IF ... THEN ... ELSE statement
(c) the CASE statement
(d) the FOR loop
(e) the MOD operator.
8.28 Repeat the last exercise for the language suggested by Exercise 8.25, using syntax that resembles that
found in C++.
8.29 In Modula-2, structured statements are each terminated with their own END. How would you have to
change the Clang language definition to use Modula-2 forms for the existing statements, and for the
extensions suggested in Exercise 8.27? What advantages, if any, do these forms have over those found
in Pascal or C++?
8.30 Study how the specification of string tokens has been achieved in Cocol. Some languages, like Modula-
2, allow strings to be delimited by either single or double quotes, but not to contain the delimiter as a
member of the string (so that we might write "David's Helen's brother" or 'He said "Hello"', but not
'He said "That's rubbish!"'). How would you specify string tokens if these had to match those found in
Modula-2, or those found in C++ (where various escape characters are allowed within the string)?
Contents (GIF version) | Contents (Symbol Font version) | Home © P.D. Terry
 aW (1)
W
aW (1)
W  Z (2)
W
Z (2)
W  X (3)
Z
X (3)
Z  aZ (4)
X
aZ (4)
X  a (5)
Y
a (5)
Y  aa (6)
aa (6)
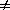 >*
>*  Y
Y for any
for any  T *).
T *).
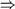 *
* 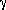
 -free grammars
-free grammars  T )* N (N
T )* N (N  |
| 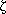
 with
with  , then we may effect a
derivation step
, then we may effect a
derivation step