 xB (1)
B
xB (1)
B  z (2)
B
z (2)
B  yB (3)
yB (3)
In this chapter we build on the ideas developed in the last one, and discuss the relationship between the formal definition of the syntax of a programming language, and the methods that can be used to parse programs written in that language. As with so much else in this text, our treatment is introductory, but detailed enough to make the reader aware of certain crucial issues.
The task of the front end of a translator is, of course, not the generation of sentences in a source language, but the recognition of them. This implies that the generating steps which led to the construction of a sentence must be deduced from the finished sentence. How difficult this is to do depends on the complexity of the production rules of the grammar. For Pascal-like languages it is, in fact, not too bad, but in the case of languages like Fortran and C++ it becomes quite complicated, for reasons that may not at first be apparent.
Many different methods for parsing sentences have been developed. We shall concentrate on a rather simple, and yet quite effective one, known as top-down parsing by recursive descent, which can be applied to Pascal, Modula-2, and many similar languages, including the simple one of section 8.7.
The reason for the phrase "by recursive descent" will become apparent later. For the moment we note that top- down methods effectively start from the goal symbol and try to regenerate the sentence by applying a sequence of appropriate productions. In doing this they are guided by looking at the next terminal in the string that they have been given to parse.
To illustrate top-down parsing, consider the toy grammar
G = { N , T , S , P }
N = { A , B }
T = { x , y , z }
S = A
P =
A  xB (1)
B
xB (1)
B  z (2)
B
z (2)
B  yB (3)
yB (3)
Let us try to parse the sentence xyyz, which clearly is formed from the terminals of this grammar. We start with the goal symbol and the input string
Sentential form S = A Input string xyyz
To the sentential form A we apply the only possible production (1) to get
Sentential form xB Input string xyyz
So far we are obviously doing well. The leading terminals in both the sentential form and the input string match, and we can effectively discard them from both; what then remains implies that from the non-terminal B we must be able to derive yyz.
Sentential form B Input string yyz
We could choose either of productions (2) or (3) in handling the non-terminal B; simply looking at the input string indicates that (3) is the obvious choice. If we apply this production we get
Sentential form yB Input string yyz
which implies that from the non-terminal B we must be able to derive yz.
Sentential form B Input string yz
Again we are led to use production (3) and we get
Sentential form yB Input string yz
which implies that from the non-terminal B we must be able to derive the terminal z directly - which of course we can do by applying (2).
The reader can easily verify that a sentence composed only of the terminal x (such as xxxx) could not be derived from the goal symbol, nor could one with y as the rightmost symbol, such as xyyyy.
The method we are using is a special case of so-called LL(k) parsing. The terminology comes from the notion that we are scanning the input string from Left to right (the first L), applying productions to the Leftmost non- terminal in the sentential form we are manipulating (the second L), and looking only as far ahead as the next k terminals in the input string to help decide which production to apply at any stage. In our example, fairly obviously, k = 1; LL(1) parsing is the most common form of LL(k) parsing in practice.
Parsing in this way is not always as easy, as is evident from the following example
G = { N , T , S , P }
N = { A , B , C }
T = { x , y , z }
S = A
P =
A  xB (1)
A
xB (1)
A  xC (2)
B
xC (2)
B  xB (3)
B
xB (3)
B  y (4)
C
y (4)
C  xC (5)
C
xC (5)
C  z (6)
z (6)
If we try to parse the sentence xxxz we might proceed as follows
Sentential form S = A Input string xxxz
In manipulating the sentential form A we must make a choice between productions (1) and (2). We do not get any real help from looking at the first terminal in the input string, so let us try production (1). This leads to
Sentential form xB Input string xxxz
which implies that we must be able to derive xxz from B. We now have a much clearer choice; of the productions for B it is (3) which will yield an initial x, so we apply it and get to
Sentential form xB Input string xxz
which implies that we must be able to derive xz from B. If we apply (1) again we get
Sentential form xB Input string xz
which implies that we must be able to derive z directly from B, which we cannot do. If we reflect on this we see that either we cannot derive the string, or we made a wrong decision somewhere along the line. In this case, fairly obviously, we went wrong right at the beginning. Had we used production (2) and not (1) we should have matched the string quite easily.
When faced with this sort of dilemma, a parser might adopt the strategy of simply proceeding according to one of the possible options, being prepared to retreat along the chosen path if no further progress is possible. Any backtracking action is clearly inefficient, and even with a grammar as simple as this there is almost no limit to the amount of backtracking one might have to be prepared to do. One approach to language design suggests that syntactic structures which can only be described by productions that run the risk of requiring backtracking algorithms should be identified, and avoided.
This may not be possible after the event of defining a language, of course - Fortran is full of examples where it seems backtracking might be needed. A classic example is found in the pair of statements
DO 10 I = 1 , 2
and
DO 10 I = 1 . 2
These are distinguishable as examples of two totally different statement types (DO statement and REAL assignment) only by the period/comma. This kind of problem is avoided in modern languages by the introduction of reserved keywords, and by an insistence that white space appear between some tokens (neither of which are features of Fortran, but neither of which cause difficulties for programmers who have never known otherwise).
The consequences of backtracking for full-blooded translators are far more severe than our simple example might suggest. Typically these do not simply read single characters (even "unreading" characters is awkward enough for a computer), but also construct explicit or implicit trees, generate code, create symbol tables and so on - all of which may have to be undone, perhaps just to be redone in a very slightly different way. In addition, backtracking makes the detection of malformed sentences more complicated. All in all, it is best avoided.
In other words, we should like to be able to confine ourselves to the use of deterministic parsing methods, that is, ones where at each stage we can be sure of which production to apply next - or, where, if we cannot find a production to use, we can be sure that the input string is malformed.
It might occur to the reader that some of these problems - including some real ones too, like the Fortran example just given - could be resolved by looking ahead more than one symbol in the input string. Perhaps in our toy problem we should have been prepared to scan four symbols ahead? A little more reflection shows that even this is quite futile. The language which this grammar generates can be described by:
L(G) = { xn p | n > 0, p{y , z} }
or, if the reader prefers less formality:
"at least one, but otherwise as many x's in a row as you like, followed by a single y or z"
We note that being prepared to look more than one terminal ahead is a strategy which can work well in some situations (Parr and Quong, 1996), although, like backtracking, it will clearly be more difficult to implement.
The top-down approach to parsing looks so promising that we should consider what restrictions have to be placed on a grammar so as to allow us to use the LL(1) approach (and its close cousin, the method of recursive descent). Once these have been established we shall pause to consider the effects they might have on the design or specification of "real" languages.
A little reflection on the examples above will show that the problems arise when we have alternative productions for the next (left-most) non-terminal in a sentential form, and should lead to the insight that the initial symbols that can be derived from the alternative right sides of the production for a given non-terminal must be distinct.
 -free grammars
-free grammars To enhance the discussion, we introduce the concept of the terminal start symbols of a non-terminal: the set FIRST(A) of the non-terminal A is defined to be the set of all terminals with which a string derived from A can start, that is
aFIRST(A) if A
+ a
9 (A
N ; a
T ;
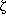
(N
T )* )
 -productions, as we shall see, are a source of complication; for the moment we note that for a unique production
of the form A
-productions, as we shall see, are a source of complication; for the moment we note that for a unique production
of the form A 
 , FIRST(A) = �.
, FIRST(A) = �.
In fact we need to go further, and so we introduce the related concept of the terminal start symbols of a general
string 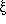 in a similar way, as the set of all terminals with which
in a similar way, as the set of all terminals with which 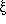 or a string derived from
or a string derived from 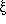 can start, that is
can start, that is
aFIRST(
) if
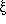
* a
(a
T ;
,
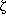
(N
T )* )
again with the ad hoc rule that FIRST( ) = �. Note that
) = �. Note that  is not a member of the terminal vocabulary T, and
that it is important to distinguish between FIRST(
is not a member of the terminal vocabulary T, and
that it is important to distinguish between FIRST(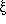 ) and FIRST(A). The string
) and FIRST(A). The string 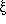 might consist of a single non-
terminal A, but in general it might be a concatenation of several symbols.
might consist of a single non-
terminal A, but in general it might be a concatenation of several symbols.
With the aid of these we may express a rule that easily allows us to determine when an  -free grammar is LL(1):
-free grammar is LL(1):
Rule 1
When the productions for any non-terminal A admit alternatives
A
1 |
2 | . . .
n
but where
k
>
for any k, the sets of initial terminal symbols of all strings that can be generated from each of the
k's must be disjoint, that is
FIRST(j)
FIRST(
k) = � for all j
k
If all the alternatives for a non-terminal A were simply of the form
k = ak
k (ak
T ;
k ,
k
(N
T )* )
it would be easy to check the grammar very quickly. All productions would have right-hand sides starting with a
terminal, and obviously FIRST(ak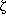 k) = { ak }.
k) = { ak }.
It is a little restrictive to expect that we can write or rewrite all productions with alternatives in this form. More likely we shall find several alternatives of the form
k = Bk
k
where Bk is another non-terminal. In this case to find FIRST(Bk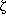 k) we shall have to consider the production rules
for Bk, and look at the first terminals which can arise from those (and so it goes on, because there may be
alternatives all down the line). All of these must be added to the set FIRST(
k) we shall have to consider the production rules
for Bk, and look at the first terminals which can arise from those (and so it goes on, because there may be
alternatives all down the line). All of these must be added to the set FIRST(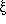 k). Yet another complication arises
if Bk is nullable, that is, if Bk
k). Yet another complication arises
if Bk is nullable, that is, if Bk 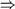 *
*  , because in that case we have to add FIRST(
, because in that case we have to add FIRST(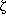 k) into the set FIRST(
k) into the set FIRST(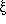 k) as
well.
k) as
well.
The whole process of finding the required sets may be summarized as follows:
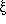 k is a terminal, then FIRST(
k is a terminal, then FIRST(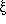 k) is of the form
FIRST(ak
k) is of the form
FIRST(ak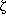 k), and then FIRST(ak
k), and then FIRST(ak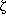 k) = { ak }.
k) = { ak }.
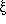 k is a non-terminal, then FIRST(
k is a non-terminal, then FIRST(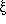 k) is of the form
FIRST(Bk
k) is of the form
FIRST(Bk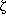 k). If Bk is a non-terminal with the derivation rule
k). If Bk is a non-terminal with the derivation rule
Bk
k1 |
k2 | . . . . |
kn
then
FIRST(k) = FIRST(Bk
k) = FIRST(
k1)
FIRST(
k2) . . .
FIRST(
kn)
with the addition that if any  kj is capable of generating the null string, then the set
FIRST(
kj is capable of generating the null string, then the set
FIRST(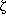 k) has to be included in the set FIRST(
k) has to be included in the set FIRST(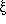 k) as well.
k) as well.
G = { N , T , S , P }
N = { A , B , C }
T = { x , y , z }
S = A
P =
A  B (1)
A
B (1)
A  C (2)
B
C (2)
B  xB (3)
B
xB (3)
B  y (4)
C
y (4)
C  xC (5)
C
xC (5)
C  z (6)
z (6)
This generates exciting sentences with any number of x's, followed by a single y or z. On looking at the alternatives for the non-terminal A we see that
FIRST(A1) = FIRST(B) = FIRST(xB)FIRST(y) = { x , y }
FIRST(A2) = FIRST(C) = FIRST(xC)FIRST(z) = { x , z }
so that Rule 1 is violated, as both FIRST(B) and FIRST(C) have x as a member.
 -free grammars
-free grammars
We have already commented that  -productions might cause difficulties in parsing. Indeed, Rule 1 is not strong
enough to detect another source of trouble, which may arise if such productions are used. Consider the grammar
-productions might cause difficulties in parsing. Indeed, Rule 1 is not strong
enough to detect another source of trouble, which may arise if such productions are used. Consider the grammar
G = { N , T , S , P }
N = { A , B }
T = { x , y }
S = A
P =
A  Bx (1)
B
Bx (1)
B  xy (2)
B
xy (2)
B 
 (3)
(3)
In terms of the discussion above, Rule 1 is satisfied. Of the alternatives for the non-terminal B, we see that
FIRST(B1) = FIRST(xy) = x
FIRST(B2) = FIRST() = �
which are disjoint. However, if we try to parse the string x we may come unstuck
Sentential form S = A Input string x
Sentential form Bx Input string x
As we are working from left to right and have a non-terminal on the left we substitute for B, to get, perhaps
Sentential form xyx Input string x
which is clearly wrong. We should have used (3), not (2), but we had no way of telling this on the basis of looking at only the next terminal in the input.
This situation is called the null string problem, and it arises only for productions which can generate the null
string. One might try to rewrite the grammar so as to avoid  -productions, but in fact that is not always
necessary, and, as we have commented, it is sometimes highly inconvenient. With a little insight we should be
able to see that if a non-terminal is nullable, we need to examine the terminals that might legitimately follow it,
before deciding that the
-productions, but in fact that is not always
necessary, and, as we have commented, it is sometimes highly inconvenient. With a little insight we should be
able to see that if a non-terminal is nullable, we need to examine the terminals that might legitimately follow it,
before deciding that the  -production is to be applied. With this in mind it is convenient to define the terminal
successors of a non-terminal A as the set of all terminals that can follow A in any sentential form, that is
-production is to be applied. With this in mind it is convenient to define the terminal
successors of a non-terminal A as the set of all terminals that can follow A in any sentential form, that is
aFOLLOW(A) if S
*
Aa
(A, S
N ; a
T ;
,
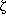
(N
T )* )
To handle this situation, we impose the further restriction
Rule 2
When the productions for a non-terminal A admit alternatives
A
1 |
2 | . . .
n
and in particular where
k
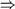
for some k, the sets of initial terminal symbols of all sentences that can be generated from each of the
j for j
k must be disjoint from the set FOLLOW(A) of symbols that may follow any sequence generated from A, that is
FIRST(j)
FOLLOW(A) = �, j
k
or, rather more loosely,
FIRST(A)FOLLOW(A) = �
where, as might be expected
FIRST(A) = FIRST(1)
FIRST(
2)
. . . FIRST(
n )
In practical terms, the set FOLLOW(A) is computed by considering every production Pk of the form
Pk
k A
k
and forming the sets FIRST(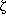 k), when
k), when
FOLLOW(A) = FIRST(1)
FIRST(
2)
. . .
FIRST(
n)
with the addition that if any 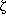 k is also capable of generating the null string, then the set FOLLOW(Pk) has to
be included in the set FOLLOW(A) as well.
k is also capable of generating the null string, then the set FOLLOW(Pk) has to
be included in the set FOLLOW(A) as well.
In the example given earlier, Rule 2 is clearly violated, because
FIRST(B1) = FIRST(xy) = { x } = FOLLOW(B)
It is important to note two points that may have slipped the reader's attention:
 -productions as alternatives, Rule 2 applies in addition to Rule
1. Although we stated Rule 1 as applicable to
-productions as alternatives, Rule 2 applies in addition to Rule
1. Although we stated Rule 1 as applicable to  -free grammars, it is in fact a necessary (but not
sufficient) condition that any grammar must meet in order to satisfy the LL(1) conditions.
-free grammars, it is in fact a necessary (but not
sufficient) condition that any grammar must meet in order to satisfy the LL(1) conditions.
It may be worth studying a further example so as to explore these rules further. Consider the language defined by the grammar
G = { N , T , S , P }
N = { A , B , C , D }
T = { w , x , y , z }
S = A
P =
A  BD | CB (1, 2)
B
BD | CB (1, 2)
B  x B z | y |
x B z | y |  (3, 4, 5)
C
(3, 4, 5)
C  w | z (6, 7)
D
w | z (6, 7)
D  x | z (8, 9)
x | z (8, 9)
All four non-terminals admit to alternatives, and B is capable of generating the empty string  . Rule 1 is clearly
satisfied for the alternative productions for B, C and D, since these alternatives all produce sentential forms that
start with distinctive terminals.
. Rule 1 is clearly
satisfied for the alternative productions for B, C and D, since these alternatives all produce sentential forms that
start with distinctive terminals.
To check Rule 1 for the alternatives for A requires a little more work. We need to examine the intersection of FIRST(BD) and FIRST(CB).
FIRST(CB) is simply FIRST(C) = { w }  { z } = { w , z }.
{ z } = { w , z }.
FIRST(BD) is not simply FIRST(B), since B is nullable. Applying our rules to this situation leads to the result
that FIRST(BD) = FIRST(B)  FIRST(D) = ( { x }
FIRST(D) = ( { x }  { y } )
{ y } )  ( { x }
( { x }  { z } ) = { x , y , z }.
{ z } ) = { x , y , z }.
Since FIRST(CB) 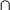 FIRST(BD) = { z }, Rule 1 is broken and the grammar is non-LL(1). Just for completeness,
let us check Rule 2 for the productions for B. We have already noted that FIRST(B) = { x , y }. To compute
FOLLOW(B) we need to consider all productions where B appears on the right side. These are productions (1),
(2) and (3). This leads to the result that
FIRST(BD) = { z }, Rule 1 is broken and the grammar is non-LL(1). Just for completeness,
let us check Rule 2 for the productions for B. We have already noted that FIRST(B) = { x , y }. To compute
FOLLOW(B) we need to consider all productions where B appears on the right side. These are productions (1),
(2) and (3). This leads to the result that
FOLLOW(B) = FIRST(D) (from the rule A  BD)
BD)
 FOLLOW(A) (from the rule A
FOLLOW(A) (from the rule A  CB)
CB)
 FIRST(z) (from the rule B
FIRST(z) (from the rule B  xBz)
= { x , z }
xBz)
= { x , z }  �
�  { z } = { x , z }
{ z } = { x , z }
Since FIRST(B) 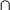 FOLLOW(B) = { x , y }
FOLLOW(B) = { x , y } 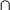 { x , z } = { x }, Rule 2 is broken as well.
{ x , z } = { x }, Rule 2 is broken as well.
The rules derived in this section have been expressed in terms of regular BNF notation, and we have so far avoided discussing whether they might need modification in cases where the productions are expressed in terms of the option and repetition (closure) metasymbols ( [ ] and { } respectively). While it is possible to extend the discussion further, it is not really necessary, in a theoretical sense, to do so. Grammars that are expressed in terms of these symbols are easily rewritten into standard BNF by the introduction of extra non-terminals. For example, the set of productions
A
[
]
B
{
}
is readily seen to be equivalent to
A
C
B
D
C
|
D
D |
to which the rules as given earlier are easily applied (note that the production for D is right recursive). In effect, of course, these rules amount to saying for this example that
FIRST()
FIRST(
) = �
FIRST()
FIRST(
) = �
with the proviso that if 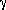 or
or  are nullable, then we must add conditions like
are nullable, then we must add conditions like
FIRST()
FOLLOW(A) = �
FIRST()
FOLLOW(B) = �
There are a few other points that are worth making before closing this discussion.
The reader can probably foresee that in a really large grammar one might have to make many iterations over the productions in forming all the FIRST and FOLLOW sets and in checking the applications of all these rules. Fortunately software tools are available to help in this regard - any reasonable LL(1) compiler generator like Coco/R must incorporate such facilities.
A difficulty might come about in automatically applying the rules to a grammar with which it is possible to derive the empty string. A trivial example of this is provided by
G = { N , T , S , P }
N = { A }
T = { x , y }
S = A
P =
A  xy (1)
A
xy (1)
A 
 (2)
(2)
Here the nullable non-terminal A admits to alternatives. In trying to determine FOLLOW(A) we should reach the uncomfortable conclusion that this was not really defined, as there are no productions in which A appears on the right side. Situations like this are usually handled by constructing a so-called augmented grammar, by adding a new terminal symbol (denoted, say, by #), a new goal symbol, and a new single production. For the above example we would create an augmented grammar on the lines of
G = { N , T , S , P }
N = { A, B }
T = { x , y, # }
S = B
P =
B  A # (1)
A
A # (1)
A  xy (2)
A
xy (2)
A 
 (3)
(3)
The new terminal # amounts to an explicit end-of-file or end-of-string symbol; we note that realistic parsers and scanners must always be able to detect and react to an end-of-file in a sensible way, so that augmenting a grammar in this way really carries no practical overheads.
The two rules for determining whether a grammar is LL(1) are sometimes found stated in other ways (which are, of course, equivalent). Some authors combine them as follows:
Combined LL(1) Rule
A grammar is LL(1) if for every non-terminal A that admits alternatives
A
1 |
2 | . . .
n
the following holds
FIRST(j � FOLLOW(A))
FIRST(
k � FOLLOW(A)) = �, j
k
where � denotes "composition" in the mathematical sense. Here the cases  j
j 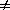 >
>  and
and  j
j 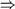
 are combined -
for
are combined -
for  j
j 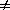 >*
>*  we have that FIRST(
we have that FIRST(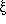 j � FOLLOW(A)) = FIRST(
j � FOLLOW(A)) = FIRST(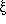 j), while for
j), while for  j
j 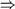 *
*  we have similarly that
FIRST(
we have similarly that
FIRST(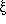 j � FOLLOW(A)) = FOLLOW(A) .
j � FOLLOW(A)) = FOLLOW(A) .
Other authors conduct this discussion in terms of the concept of director sets. For every non-terminal A that admits to alternative productions of the form
A
1 |
2 | . . . |
n
we define DS(A,  k) for each alternative to be the set which helps choose whether to use the alternative; when the
input string contains the terminal a we choose
k) for each alternative to be the set which helps choose whether to use the alternative; when the
input string contains the terminal a we choose  k such that a
k such that a  DS(A,
DS(A,  k). The LL(1) condition is then
k). The LL(1) condition is then
DS(A,j)
DS(A,
k) = �, j
k
The director sets are found from the relation
aDS(A,
k) if either a
FIRST(
k) (if
k
>*
)
or aFOLLOW(A) (if
k
*
)
9.1 Test the following grammar for being LL(1)
G = { N , T , S , P }
N = { A , B }
T = { w , x , y , z }
S = A
P =
A  B ( x | z ) | ( w | z ) B
B
B ( x | z ) | ( w | z ) B
B  x B z | { y }
x B z | { y }
9.2 Show that the grammar describing EBNF itself (section 5.9.1) is LL(1).
9.3 The grammar for EBNF as presented in section 5.9.1 does not allow an implicit  to appear in a
production, although the discussion in that section implied that this was often found in practice. What
change could you make to the grammar to allow an implicit
to appear in a
production, although the discussion in that section implied that this was often found in practice. What
change could you make to the grammar to allow an implicit  ? Is your resulting grammar still LL(1)? If
not, can you find a formulation that is LL(1)?
? Is your resulting grammar still LL(1)? If
not, can you find a formulation that is LL(1)?
9.4 In section 8.7.2, constant declarations in Clang were described by the productions
ConstDeclarations = "CONST" OneConst { OneConst } .
OneConst = identifier "=" number ";" .
Is this part of the grammar LL(1)? What would be the effect if one were to factorize the grammar
ConstDeclarations = "CONST" OneConst { ";" OneConst } ";" .
OneConst = identifier "=" number .
9.5 As a more interesting example of applying an analysis to a grammar expressed in EBNF, let us consider how we might describe the theatrical production of a Shakespearian play with five acts. In each act there may be several scenes, and in each scene appear one or more actors, who gesticulate and make speeches to one another (for the benefit of the audience, of course). Actors come onto the stage at the start of each scene, and come and go as the scene proceeds - to all intents and purposes between speeches - finally leaving at the end of the scene (in the Tragedies some may leave dead, but even these usually revive themselves in time to go home). Plays are usually staged with an interval between the third and fourth acts.
Actions like "speech", "entry" and "exit" are really in the category of the lexical terminals which a scanner (in the person of a member of the audience) would recognize as key symbols while watching a play. So one description of such a staged play might be on the lines of
Play = Act Act Act "interval" Act Act .
Act = Scene { Scene } .
Scene = { "speech" } "entry" { Action } .
Action = "speech" | "entry" | "exit" | "death" | "gesticulation" .
This does not require all the actors to leave at the end of any scene (sometimes this does not happen in real life, either). We could try to get this effect by writing
Scene = { "speech" } "entry" { Action } { "exit" } .
but note that this context-free grammar cannot force as many actors to leave as entered - in computer language terms the reader should recognize this as the same problem as being unable to specify that the number of formal and actual parameters to a procedure agree.
Analyse this grammar in detail. If it proves out to be non-LL(1), try to find an equivalent that is LL(1), or argue why this should be impossible.
There are some immediate implications which follow from the rules of the last section as regards language design and specification. Alternative right-hand sides for productions are very common; we cannot hope to avoid their use in practice. Let us consider some common situations where problems might arise, and see whether we can ensure that the conditions are met.
Firstly, we should note that we cannot hope to transform every non-LL(1) grammar into an equivalent LL(1) grammar. To take an extreme example, an ambiguous grammar must have two parse trees for at least one input sentence. If we really want to allow this we shall not be able to use a parsing method that is capable of finding only one parse tree, as deterministic parsers must do. We can argue that an ambiguous grammar is of little interest, but the reader should not go away with the impression that it is just a matter of trial and error before an equivalent LL(1) grammar is found for an arbitrary grammar.
Often a combination of substitution and re-factorization will resolve problems. For example, it is almost trivially easy to find a grammar for the problematic language of section 9.1 which satisfies Rule 1. Once we have seen the types of strings the language allows, then we easily see that all we have to do is to find productions that sensibly deal with leading strings of x's, but delay introducing y and z for as long as possible. This insight leads to productions of the form
A  xA | C
C
xA | C
C  y | z
y | z
Productions with alternatives are often found in specifying the kinds of Statement that a programming language may have. Rule 1 suggests that if we wish to parse programs in such a language by using LL(1) techniques we should design the language so that each statement type begins with a different reserved keyword. This is what is attempted in several languages, but it is not always convenient, and we may have to get round the problem by factorizing the grammar differently.
As another example, if we were to extend the language of section 8.7 we might contemplate introducing REPEAT loops in one of two forms
RepeatStatement = "REPEAT" StatementSequence "UNTIL" Condition
| "REPEAT" StatementSequence "FOREVER" .
Both of these start with the reserved word REPEAT. However, if we define
RepeatStatement = "REPEAT" StatementSequence TailRepeatStatement .
TailRepeatStatement = "UNTIL" Condition | "FOREVER" .
parsing can proceed quite happily. Another case which probably comes to mind is provided by the statements
Statement = IfStatement | OtherStatement .
IfStatement = "IF" Condition "THEN" Statement
| "IF" Condition "THEN" Statement "ELSE" Statement .
Factorization on the same lines as for the REPEAT loop is less successful. We might be tempted to try
Statement = IfStatement | OtherStatement . (1, 2)
IfStatement = "IF" Condition "THEN" Statement IfTail . (3)
IfTail = "ELSE" Statement |  . (4, 5)
. (4, 5)
but then we run foul of Rule 2. The production for IfTail is nullable; a little reflection shows that
FIRST("ELSE" Statement) = { "ELSE" }
while to compute FOLLOW(IfTail) we consider the production (3) (which is where IfTail appears on the right side), and obtain
FOLLOW(IfTail) = FOLLOW(IfStatement) (production 3)
= FOLLOW(Statement) (production 1)
which clearly includes ELSE.
The reader will recognize this as the "dangling else" problem again. We have already remarked that we can find ways of expressing this construct unambiguously; but in fact the more usual solution is just to impose the semantic meaning that the ELSE is attached to the most recent unmatched THEN, which, as the reader will discover, is handled trivially easily by a recursive descent parser. (Semantic resolution is quite often used to handle tricky points in recursive descent parsers, as we shall see.)
Perhaps not quite so obviously, Rule 1 eliminates the possibility of using left recursion to specify syntax. This is a very common way of expressing a repeated pattern of symbols in BNF. For example, the two productions
AB | AB
describe the set of sequences B , BB , BBB ... . Their use is now ruled out by Rule 1, because
FIRST(A1) = FIRST(B)
FIRST(A2) = FIRST(AB) = FIRST(A) = FIRST(B)FIRST(AB)
FIRST(A1)FIRST(A2)
�
Direct left recursion can be avoided by using right recursion. Care must be taken, as sometimes the resulting grammar is still unsuitable. For example, the productions above are equivalent to
AB | BA
but this still more clearly violates Rule 1. In this case, the secret lies in deliberately introducing extra non- terminals. A non-terminal which admits to left recursive productions will in general have two alternative productions, of the form
AAX | Y
By expansion we can see that this leads to sentential forms like
Y , YX , YXX , YXXX
and these can easily be derived by the equivalent grammar
AYZ
Z
| XZ
The example given earlier is easily dealt with in this way by writing X = Y = B, that is
ABZ
Z
| BZ
The reader might complain that the limitation on two alternatives for A is too severe. This is not really true, as suitable factorization can allow X and Y to have alternatives, none of which start with A. For example, the set of productions
AAb | Ac | d | e
can obviously be recast as
AAX | Y
Xb | c
Yd | e
(Indirect left recursion, for example
AB
BC . . .
CA . . .
is harder to handle, and is, fortunately, not very common in practice.)
This might not be quite as useful as it first appears. For example, the problem with
Expression = Expression "-" Term | Term .
can readily be removed by using right recursion
Expression = Term RestExpression .
RestExpression =  | "-" Term RestExpression .
| "-" Term RestExpression .
but this may have the side-effect of altering the implied order of evaluation of an Expression. For example, adding the productions
Term = "x" | "y" | "z" .
to the above would mean that with the former production for Expression, a string of the form x - y - z would be evaluated as (x - y) - z. With the latter production it might be evaluated as x - (y - z), which would result in a very different answer (unless z were zero).
The way to handle this situation would be to write the parsing algorithms to use iteration, as introduced earlier, for example
Expression = Term { "-" Term } .
Although this is merely another way of expressing the right recursive productions used above, it may be easier for the reader to follow. It carries the further advantage of more easily retaining the left associativity which the "-" terminal normally implies.
It might be tempting to try to use such iteration to remove all the problems associated with recursion. Again, care
must be taken, since this action often implies that  -productions either explicitly or implicitly enter the grammar.
For example, the construction
-productions either explicitly or implicitly enter the grammar.
For example, the construction
A{ B }
actually implies, and can be written
A
| B A
but can only be handled if FIRST(B) 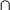 FOLLOW(A) = �. The reader might already have realized that all our
manipulations to handle Expression would come to naught if "-" could follow Expression in other productions
of the grammar.
FOLLOW(A) = �. The reader might already have realized that all our
manipulations to handle Expression would come to naught if "-" could follow Expression in other productions
of the grammar.
9.6 Determine the FIRST and FOLLOW sets for the following non-terminals of the grammar defined in various ways in section 8.7, and comment on which formulations may be parsed using LL(1) techniques.
Block
ConstDeclarations
VarDeclarations
Statement
Expression
Factor
Term
9.7 What are the semantic implications of using the productions suggested in section 8.4 for the IF ... THEN and IF ... THEN ... ELSE statements?
9.8 Whether to regard the semicolon as a separator or as a terminator has been a matter of some controversy. Do we need semicolons at all in a language like the one suggested in section 8.7? Try to write productions for a version of the language where they are simply omitted, and check whether the grammar you produce satisfies the LL(1) conditions. If it does not, try to modify the grammar until it does satisfy these conditions.
9.9 A close look at the syntax of Pascal, Modula-2 or the language of section 8.7 shows that an  -production
is allowed for Statement. Can you think of any reasons at all why one should not simply forbid empty
statements?
-production
is allowed for Statement. Can you think of any reasons at all why one should not simply forbid empty
statements?
9.10 Write down a set of productions that describes the form that REAL literal constants may assume in Pascal, and check to see whether they satisfy the LL(1) conditions. Repeat the exercise for REAL literal constants in Modula-2 and for float literals in C++ (surprisingly, perhaps, the grammars are different).
9.11 In a language like Modula-2 or Pascal there are two classes of statements that start with identifiers, namely assignment statements and procedure calls. Is it possible to find a grammar that allows this potential LL(1) conflict to be resolved? Does the problem arise in C++?
9.12 A full description of C or C++ is not possible with an LL(1) grammar. How large a subset of these languages could one describe with an LL(1) grammar?
9.13 C++ and Modula-2 are actually fairly close in many respects - both are imperative, both have the same sorts of statements, both allow user defined data structures, both have functions and procedures. What features of C++ make description in terms of LL(1) grammars difficult or impossible, and is it easier or more difficult to describe the corresponding features in Modula-2? Why?
9.14 Why do you suppose C++ has so many levels of precedence and the rules it does have for associativity? What do they offer to a programmer that Modula-2 might appear to withhold? Does Modula-2 really withhold these features?
9.15 Do you suppose there may be any correlation between the difficulty of writing a grammar for a language (which programmers do not usually try to do) and learning to write programs in that language (which programmers often do)?
Good treatments of the material in this chapter may be found at a comprehensible level in the books by Wirth (1976b, 1996), Welsh and McKeag (1980), Hunter (1985), Gough (1988), Rechenberg and Mössenböck (1989), and Tremblay and Sorenson (1985). Pittman and Peters (1992) have a good discussion of what can be done to transform non-LL(k) grammars into LL(k) ones.
Algorithms exist for the detection and elimination of useless productions. For a discussion of these the reader is referred to the books by Gough (1988), Rechenberg and Mössenböck (1989), and Tremblay and Sorenson (1985).
Our treatment of the LL(1) conditions may have left the reader wondering whether the process of checking them - especially the second one - ever converges for a grammar with anything like the number of productions needed to describe a real programming language. In fact, a little thought should suggest that, even though the number of sentences which they can generate might be infinite, convergence should be guaranteed, since the number of productions is finite. The process of checking the LL(k) conditions can be automated, and algorithms for doing this and further discussion of convergence can be found in the books mentioned above.