Contents (GIF version) | Contents (Symbol Font version) | Home © P.D. Terry
17 PARAMETERS AND FUNCTIONS
It is the aim of this chapter to show how we can extend our language and its compiler to allow for value-returning
functions in addition to regular procedures, and to support the use of parameters. Once again, the syntactic and
semantic extensions we shall make are kept as simple as possible, and should be familiar to the reader from a
study of other imperative languages.
17.1 Syntax and semantics
The subject of parameter passing is fairly extensive, as the reader may have realized. In the development of
programming languages several models of parameter passing have been proposed, and the ones actually
implemented vary semantically from language to language, while syntactically often appearing deceptively
similar. In most cases, declaration of a subprogram segment is accompanied by the declaration of a list of formal
parameters, which appear to have a status within the subprogram rather like that of local variables. Invocation of
the subprogram is accompanied by a corresponding list of actual parameters (sometimes called arguments), and
it is invariably the case that the relationship between formal and actual parameters is achieved by positional
correspondence, rather than by lexical correspondence in the source text. Thus it would be quite legal, if a little
confusing to another reader, to declare
PROCEDURE AnyName ( A , B )
and then to invoke it with a statement of the form
AnyName ( B , A )
when the A in the procedure would be associated with the B in the calling routine, and the B in the procedure
would be associated with the A in the calling routine. It may be the lack of name correspondence that is at the
root of a great deal of confusion in parameter handling amongst beginners.
The correspondence of formal and actual parameters goes deeper than mere position in a parameter list. Of the
various ways in which it might be established, the two most widely used and familiar parameter passing
mechanisms are those known as call-by-reference and call-by-value. In developing the case studies in this text
we have, of course, made frequent use of both of methods; we turn now to a discussion of how they are
implemented.
The semantics and the implementation of the two mechanisms are quite different:
- In call-by-reference an actual parameter usually takes the form of a VariableDesignator. Within the
subprogram, a reference to the formal parameter results, at run-time, in a direct reference to the variable
designated by the actual parameter, and any change to that formal parameter results in an immediate change
to the corresponding actual parameter. In a very real sense, a formal parameter name may be regarded as an
alias for the actual parameter name. The alias lasts as long as the procedure is active, and may be
transmitted to other subprograms with parameters passed in the same way. Call-by-reference is usually
accomplished by passing the address associated with the actual parameter to the subprogram for processing.
- In call-by-value, an actual parameter takes the form of an Expression. Formal parameters in a subprogram
(when declared in this way) are effectively variables local to that subprogram, which start their lives
initialized to the values of the corresponding actual parameter expressions. However, any changes made to
the values of the formal parameter variables are confined to the subprogram, and cannot be transmitted back
via the formal parameters to the calling routine. Fairly obviously, it is the run-time value of the expression
which is handed over to the subprogram for processing, rather than an explicit address of a variable.
Call-by-value is preferred for many applications - for example it is useful to be able to pass expressions to
procedures like WRITE without having to store their values in otherwise redundant variables. However, if an array
is passed by value, a complete copy of the array must be passed to the subprogram. This is expensive, both in
terms of space and time, and thus many programmers pass all array parameters by reference, even if there is no
need for the contents of the array to be modified. In C++, arrays may only be passed as reference parameters,
although C++ permits the use of the qualifier const to prevent an array from being modified in a subprogram.
Some languages permit call-by-reference to take place with actual parameters that are expressions in the general
sense; in this case the value of the expression is stored in a temporary variable, and the address of that variable is
passed to the subprogram.
In what follows we shall partially illustrate both methods, using syntax suggested by C. Simple scalar parameters
will be passed by value, and array parameters will be passed by reference in a way that almost models the open
array mechanism in Modula-2.
We describe the introduction of function and parameter declarations to our language more formally by the
following EBNF. The productions are highly non-LL(1), and it should not take much imagination to appreciate
that there is now a large amount of context-sensitive information that a practical parser will need to handle
(through the usual device of the symbol table). Our productions attempt to depict where such context-sensitivity
occurs.
ProcDeclaration = ( "PROCEDURE" ProcIdentifier | "FUNCTION" FuncIdentifier )
[ FormalParameters ] ";"
Block ";" .
FormalParameters = "(" OneFormal { "," OneFormal } ")" .
OneFormal = ScalarFormal | ArrayFormal .
ScalarFormal = ParIdentifier .
ArrayFormal = ParIdentifier "[" "]" .
We extend the syntax for ProcedureCall to allow procedures to be invoked with parameters:
ProcedureCall = ProcIdentifier ActualParameters .
ActualParameters = [ "(" OneActual { "," OneActual } ")" ] .
OneActual = ValueParameter | ReferenceParameter .
ValueParameter = Expression .
ReferenceParameter = Variable .
We also extend the definition of Factor to allow function references to be included in expressions with the
appropriate precedence:
Factor = Variable | ConstIdentifier | number
| "(" Expression ")"
| FuncIdentifier ActualParameters .
and we introduce the ReturnStatement in an obvious way:
ReturnStatement = "RETURN" [ Expression ] .
where the Expression is only needed within functions, which will be limited (as in traditional C and Pascal) to
returning scalar values only. Within a regular procedure the effect of a ReturnStatement is simply to transfer
control to the calling routine immediately; within a main program a ReturnStatement simply terminates execution.
A simple example of a Clang program that illustrates these extensions is as follows:
PROGRAM Debug;
FUNCTION Last (List[], Limit);
BEGIN
RETURN List[Limit];
END;
PROCEDURE Analyze (Data[], N);
VAR
LocalData[2];
BEGIN
WRITE(Last(Data, N+2), Last(LocalData, 1));
END;
VAR
GlobalData[3];
BEGIN
Analyze(GlobalData, 1);
END.
The WRITE statement in procedure Analyze would print out the value of GlobalData[3] followed by the value of
LocalData[1]. GlobalData is passed to Analyze, which refers to it under the alias of Data, and then passes it on to
Last, which, in turn, refers to it under the alias of List.
17.2 Symbol table support for context-sensitive features
It is possible to write a simple context-free set of productions that do satisfy the LL(1) constraints, and a Coco/R
generated system will require this to be done. We have remarked earlier that it is not possible to specify the
requirement that the number of formal and actual parameters must match; this will have to be done by context
conditions. So too will the requirement that each actual parameter is passed in a way compatible with the
corresponding formal parameter - for example, where a formal parameter is an open array we must not be allowed
to pass a scalar variable identifier or an expression as the actual parameter. As usual, a compiler must rely on
information stored in the symbol table to check these conditions, and we may indicate the support that must be
provided by considering the shell of a simple program:
PROGRAM Main;
VAR G1; (* global *)
PROCEDURE One (P1, P2); (* two formal scalar parameters *)
BEGIN (* body of One *)
END;
PROCEDURE Two; (* no formal parameters *)
BEGIN (* body of Two *)
END;
PROCEDURE Three (P1[]); (* one formal open array parameter *)
VAR L1, L2; (* local to Three *)
BEGIN (* body of Three *)
END;
BEGIN (* body of Main *)
END.
At the instant where the body of procedure Three is being parsed our symbol table might have a structure like that
in Figure 17.1.
.-----. .------. .------. .------.
TopScope -->|First|---->| P1 |->| L1 |->| L2 |-----------.
|-----| .->`------' `------' `------' |
|Down | | |
`-----' | .------. .------. |
| .--->| P1 |->| P2 |-------------------. |
| | | `------' `------' | |
| | `---------------------------------. | |
| | .--. | | | Sentinel
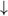 `---------------. = | | | `-->.--------.
.-----. .------. .------. .------. .-----.`---->| |
|First|---->| G1 |->| One |->| Two |->|Three|----->| |-.
|-----| `------' `------' `------' `-----' .-->`--------' |
|Down | | =
`-----' |
`---------------. = | | | `-->.--------.
.-----. .------. .------. .------. .-----.`---->| |
|First|---->| G1 |->| One |->| Two |->|Three|----->| |-.
|-----| `------' `------' `------' `-----' .-->`--------' |
|Down | | =
`-----' |
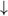 |
.-----. .------. |
|First|---->| Main |-------------------------------'
|-----| `------'
|Down |
`-----'
=
Figure 17.1 A symbol table structure with links from procedure entries to formal parameter entries
|
.-----. .------. |
|First|---->| Main |-------------------------------'
|-----| `------'
|Down |
`-----'
=
Figure 17.1 A symbol table structure with links from procedure entries to formal parameter entries
Although all three of the procedure identifiers One, Two and Three are in scope, procedures One and Two will
already have been compiled in a one-pass system. So as to retain information about their formal parameters,
internal links are set up from the symbol table nodes for the procedure identifiers to the nodes set up for these
parameters. To provide this support it is convenient to extend the definition of the TABLE_entries structure:
enum TABLE_idclasses
{ TABLE_consts, TABLE_vars, TABLE_progs, TABLE_procs, TABLE_funcs };
struct TABLE_nodes;
typedef TABLE_nodes *TABLE_index;
struct TABLE_entries {
TABLE_alfa name; // identifier
int level; // static level
TABLE_idclasses idclass; // class
union {
struct {
int value;
} c; // constants
struct {
int size, offset;
bool ref, scalar;
} v; // variables
struct {
int params, paramsize;
TABLE_index firstparam;
CGEN_labels entrypoint;
} p; // procedures, functions
};
};
Source for an implementation of the TABLE class can be found in Appendix B, and it may be helpful to draw
attention to the following features:
- Formal parameters are treated within the Block of a function or procedure in most cases as though they were
variables. So it will be convenient to enter them into the symbol table as such. However, it now becomes
necessary to tag the entry for each variable with the extra field ref. This denotes whether the identifier
denotes a true variable, or is merely an alias for a variable that has been passed to a procedure by reference.
Global and local variables and scalar formals will all have this field defined to be false.
- Passing an array to a subprogram by reference is not simply a matter of passing the address of the first
element, even though the subprogram appears to handle open arrays. We shall also need to supply the length
of the array (unless we are content to omit array bound checking). This suggests that the value of the size
field for an array formal parameter can always be 2. We observe that passing open arrays by value, as is
possible in Modula-2, is likely to be considerably more complicated.
- Formal parameter names, like local variable names, will be entered at a higher level than the procedure or
function name, so as to reserve them local status.
- For procedures and functions the params field is used to record the number of formal parameters, and the
firstparam field is used to point to the linked queue of entries for the identifiers that denote the formal
parameters. Details of the formal parameters, when needed for context-sensitive checks, can be extracted by
further member functions in the TABLE class. As it happens, for our simplified system we need only to know
whether an actual parameter must be passed by value or by reference, so a simple Boolean function isrefparam
is all that is required.
- When a subprogram identifier is first encountered, the compiler will not immediately know how many formal
parameters will be associated with it. The table handler must make provision for backpatching an entry, and
so we need a revised interface to the enter routine, as well as an update routine:
class TABLE {
public:
void enter(TABLE_entries &entry, TABLE_index &position);
// Adds entry to symbol table, and returns its position
void update(TABLE_entries &entry, TABLE_index position);
// Updates entry at known position
bool isrefparam(TABLE_entries &procentry, int n);
// Returns true if nth parameter for procentry is passed by reference
// rest as before
};
The way in which the declaration of functions and parameters is accomplished may now be understood with
reference to the following extract from a Cocol specification:
ProcDeclaration
= (. TABLE_entries entry; TABLE_index index; .)
( "PROCEDURE" (. entry.idclass = TABLE_procs; .)
| "FUNCTION" (. entry.idclass = TABLE_funcs; .)
) Ident<entry.name> (. entry.p.params = 0; entry.p.paramsize = 0;
entry.p.firstparam = NULL;
CGen->storelabel(entry.p.entrypoint);
Table->enter(entry, index);
Table->openscope(); .)
[
FormalParameters<entry> (. Table->update(entry, index); .)
] WEAK ";"
Block<entry.level+1, entry.idclass, entry.p.paramsize + CGEN_headersize>
";" .
FormalParameters<TABLE_entries &proc>
= (. TABLE_index p; .)
"(" OneFormal<proc, proc.p.firstparam>
{ WEAK "," OneFormal<proc, p> } ")" .
OneFormal<TABLE_entries &proc, TABLE_index &index>
= (. TABLE_entries formal;
formal.idclass = TABLE_vars; formal.v.ref = false;
formal.v.size = 1; formal.v.scalar = true;
formal.v.offset = proc.p.paramsize
+ CGEN_headersize + 1; .)
Ident<formal.name>
[ "[" "]" (. formal.v.size = 2; formal.v.scalar = false;
formal.v.ref = true; .)
] (. Table->enter(formal, index);
proc.p.paramsize += formal.v.size;
proc.p.params++; .) .
Address offsets have to be associated with formal parameters, as with other variables. These are allocated as the
parameters are declared. This topic is considered in more detail in the next section; for the moment notice that
parameter offsets start at CGEN_HeaderSize + 1.
17.3 Actual parameters and stack frames
There are several ways in which actual parameter values may be transmitted to a subprogram. Typically they are
pushed onto a stack as part of the activation sequence that is executed before transferring control to the procedure
or function which is to use them. Similarly, to allow a function value to be returned, it is convenient to reserve a
stack item for this just before the actual parameters are set up, and for the function subprogram to access this
reserved location using a suitable offset. The actual parameters might be stored after the frame header - that is,
within the activation record - or they might be stored before the frame header. We shall discuss this latter
possibility no further here, but leave the details as an exercise for the curious reader (see Terry (1986) or Brinch
Hansen (1985)).
If the actual parameters are to be stored within the activation record, the corresponding formal parameter offsets
are easily determined by the procedures specified by the Cocol grammar given earlier. These also keep track of
the total space that will be needed for all parameters, and the final offset reached is then passed on to the parser
for Block, which can continue to assign offsets for local variables beyond this.
To handle function returns it is simplest to have a slightly larger frame header than before. We reserve the first
location in a stack frame (that is, at an invariant offset of 1 from the base pointer BP) for a function's return value,
thereby making code generation for the ReturnStatement straightforward. This location is strictly not needed for
regular procedures, but it makes for easier code generation to keep all frame headers a constant size. We also
need to reserve an element for saving the old mark stack pointer at procedure activation so that it can be restored
once a procedure has been completed. We also need to reserve an element for saving the old mark stack pointer at
procedure activation so that it can be restored once a procedure has been completed.
If we use the display model, the arrangement of the stack after a procedure has been activated and called will
typically be as shown in Figure 17.2. The frame header and actual parameters are set up by the activation
sequence, and storage for the local variables is reserved immediately after the procedure obtains control.
<--------------- Frame Header --------------->
---------------------------------------------------------------------------
Work | Local | Actual | Mark | Return | Dynamic | Display | Return |
Space | Variables | Params | Copy | Address | Link | Copy | Value |
---------------------------------------------------------------------------
BP-5 BP-4 BP-3 BP-2 BP-1
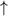 SP
SP 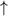 BP
Figure 17.2 Stack frame immediately after a procedure has been called
BP
Figure 17.2 Stack frame immediately after a procedure has been called
This may be made clearer by considering some examples. Figure 17.3 shows the layout in memory for the array
processing program given in section 17.1, at the instant where function Last has just started execution.
Stack Display
Address Purpose Contents Contents Level
.-> 511 ? <-------- 511 1
| 510 GlobalData[0] ? .----- 496 2
| 509 GlobalData[1] ? |
| 508 GlobalData[2] ? | frame for Debug (level 1)
.--|-> 507 GlobalData[3] ? |
| | |
| | 506 Return Value ? | ( unused )
| | 505 Display Copy 511 |
| `-- 504 Dynamic Link 511 | frame for Analyze (level 2)
| 503 Return Address 75 |
| 502 Mark pointer Copy ? |
| 501 Address of Data[0] 510 | ( address of GlobalData[0] )
| 500 Size of Data 4 | ( size of GlobalData )
| 499 Parameter N 1 |
| 498 LocalData[0] ? |
| 497 LocalData[1] ? |
| 496 LocalData[2] ? <--'<----- BP , MP
|
| 495 Return Value ?
| 494 Display Copy 507
`----- 493 Dynamic Link 507 frame for Last (level 2)
492 Return Address 45
491 Mark pointer Copy 507
490 Address of List[0] 510 ( address of GlobalData[0] )
489 Size of List 4 ( size of GlobalData )
488 Parameter Limit 3 <--------- SP
Figure 17.3 Arrangement of stack frames after calling a procedure followed by a function
Note that there are three values in the parameter area of the stack frame for Analyze. The first two are the actual
address of the first element of the array bound to the formal parameter Data, and the actual size to be associated
with this formal parameter. The third is the initial value assigned to formal parameter N. When Analyze activates
function Last it stacks the actual address of the array that was bound to Data, as well as the actual size of this
array, so as to allow Last to bind its formal parameter List to the formal parameter Data, and hence, ultimately, to
the same array (that is, to the global array GlobalData).
The second example shows a traditional, if hackneyed, approach to computing factorials:
PROGRAM Debug;
FUNCTION Factorial (M);
BEGIN
IF M <= 1 THEN RETURN 1;
RETURN M * Factorial(M-1);
END;
VAR N;
BEGIN
READ(N);
WHILE N > 0 DO
BEGIN WRITE(Factorial(N)); READ(N) END;
END.
If this program were to be supplied with a data value of N = 3, then the arrangement of stack frames would be as
depicted in Figure 17.4 immediately after the function has been called for the second time.
Stack Display
Address Purpose Contents Contents Level
.-> 511 ? <-------- 511 1
.-|-> 510 Variable N 3 .----- 502 2
| | |
| | 509 Return Value ? |
| | 508 Display Copy ? | frame for Factorial (level 2)
| `-- 507 Dynamic Link 511 |
| 506 Return Address 67 |
| 505 Mark pointer Copy ? |
| 504 Parameter M 3 |
| |
| 503 Address for product 509 | work space for Factorial
| 502 Multiplicand M 3 <--' <---- BP , MP
|
| 501 Return Value ?
| 500 Display Copy 510
`---- 499 Dynamic Link 510 frame for Factorial (level 2)
498 Return Address 38
498 Mark pointer Copy 510
497 Parameter M 2 <--------- SP
Figure 17.4 Arrangement of stack frames after making a recursive call to the Factorial function
Factorial can pick up its parameter M by using an offset of 5 from BP, and can assign the value to be returned to
the stack element whose offset is 1 from BP. (In practice the addressing might be done via Display[2], rather than
via BP).
Note that this way of returning function values is entirely consistent with the use of the stack for expression
evaluation. In practice, however, many compilers return the value of a scalar function in a machine register.
17.4 Hypothetical stack machine support for parameter passing
Little has to be added to our stack machine to support parameter passing and function handling. Leaving a Block
is slightly different: after completing a regular procedure we can cut the stack back so as to throw away the entire
stack frame, but after completing a function procedure we must leave the return value on the top of stack so that it
will be available for incorporation into the expression from which the call was instigated. This means that the
STKMC_ret instruction requires a second operand. It also turns out to be useful to introduce a STKMC_nfn instruction
that can be generated at the end of each function block to detect those situations where the flow of control
through a function never reaches a ReturnStatement (this is very hard to detect at compile-time). Taking into
account the increased size of the frame header, the operational semantics of the affected instructions become:
case STKMC_cal: // procedure entry
mem[cpu.mp - 2] = display[mem[cpu.pc]]; // save display element
mem[cpu.mp - 3] = cpu.bp; // save dynamic link
mem[cpu.mp - 4] = cpu.pc + 2; // save return address
display[mem[cpu.pc]] = cpu.mp; // update display
cpu.bp = cpu.mp; // reset base pointer
cpu.pc = mem[cpu.pc + 1]; // enter procedure
break;
case STKMC_ret: // procedure exit
display[mem[cpu.pc] - 1] = mem[cpu.bp - 2]; // restore display
cpu.mp = mem[cpu.bp - 5]; // restore mark pointer
cpu.sp = cpu.bp - mem[cpu.pc + 1]; // discard stack frame
cpu.pc = mem[cpu.bp - 4]; // get return address
cpu.bp = mem[cpu.bp - 3]; // reset base pointer
break;
case STKMC_mst:
if (inbounds(cpu.sp-STKMC_headersize)) // check space available
{ mem[cpu.sp-5] = cpu.mp; // save mark pointer
cpu.mp = cpu.sp; // set mark stack pointer
cpu.sp -= STKMC_headersize; // bump stack pointer
}
break;
case STKMC_nfn: // bad function (no return)
ps = badfun; break; // change status from running
17.5 Context sensitivity and LL(1) conflict resolution
We have already remarked that our language now contains several features that are context-sensitive, and several
that make an LL(1) description difficult. These are worth summarizing:
Statement = Assignment | ProcedureCall | ...
Assignment = Variable ":=" Expression .
ProcedureCall = ProcIdentifier ActualParameters .
Both Assignment and ProcedureCall start with an identifier. Parameters cause similar difficulties:
ActualParameters = [ "(" OneActual { "," OneActual } ")" ] .
OneActual = ValueParameter | ReferenceParameter .
ValueParameter = Expression .
ReferenceParameter = Variable .
OneActual is non-LL(1), as Expression might start with an identifier, and Variable certainly does. An Expression
ultimately contains at least one Factor:
Factor = Variable | ConstIdentifier | number
| "(" Expression ")"
| FuncIdentifier ActualParameters .
and three alternatives in Factor start with an identifier. A Variable is problematic:
Variable = VarIdentifier [ "[" Expression "]" ] .
In the context of a ReferenceParameter the optional index expression is not allowed, but in the context of all other
Factors it must be present. Finally, even the ReturnStatement becomes context-sensitive:
ReturnStatement = "RETURN" [ Expression ] .
In the context of a function Block the Expression must be present, while in the context of a regular procedure or
main program Block it must be absent.
17.6 Semantic analysis and code generation
We now turn to a consideration of how the context-sensitive issues can be handled by our parser, and code
generated for programs that include parameter passing and value returning functions. It is convenient to consider
hand-crafted and automatically generated compilers separately.
17.6.1 Semantic analysis and code generation in a hand-crafted compiler
As it happens, each of the LL(1) conflicts and context-sensitive constraints is easily handled when one writes a
hand-crafted parser. Each time an identifier is recognized it is immediately checked against the symbol table,
after which the appropriate path to follow becomes clear. We consider the hypothetical stack machine interface
once more, and in terms of simplified on-the-fly code generation, making the assumption that the source will be
free of syntactic errors. Full source code is, of course, available on the source diskette.
Drawing a distinction between assignments and procedure calls has already been discussed in section 16.1.5, and
is handled from within the parser for Statement. The parser for ProcedureCall is passed the symbol table entry
apposite to the procedure being called, and makes use of this in calling on the parser to handle that part of the
activation sequence that causes the actual parameters to be stacked before the call is made:
void PARSER::ProcedureCall(TABLE_entries entry)
// ProcedureCall = ProcIdentifier ActualParameters .
{ GetSym();
CGen->markstack(); // code for activation
ActualParameters(entry); // code to evaluate arguments
CGen->call(entry.level, entry.p.entrypoint); // code to transfer control
}
A similar extension is needed to the routine that parses a Factor:
void PARSER::Factor(void)
// Factor = Variable | ConstIdentifier | FuncIdentifier ActualParameters ..
// Variable = Designator .
{ TABLE_entries entry;
switch (SYM.sym)
{ case SCAN_identifier: // several cases arise...
Table->search(SYM.name, entry); // look it up
switch (entry.idclass) // resolve LL(1) conflict
{ case TABLE_consts:
GetSym();
CGen->stackconstant(entry.c.value); // code to load named constant
break;
case TABLE_funcs:
GetSym();
CGen->markstack(); // code for activation
ActualParameters(entry); // code to evaluate arguments
CGen->call(entry.level,
entry.p.entrypoint); // code to transfer control
break;
case TABLE_vars:
Designator(entry); // code to load address
CGen->dereference(); break; // code to load value
}
break;
// ... other cases
}
}
The parsers that handle ActualParameters and OneActual are straightforward, and make use of the extended
features in the symbol table handler to distinguish between reference and value parameters:
void PARSER::ActualParameters(TABLE_entries procentry)
// ActualParameters = [ "(" OneActual { "," OneActual } ")" ] .
{ int actual = 0;
if (SYM.sym == SCAN_lparen) // check for any arguments
{ GetSym(); OneActual(procentry, actual);
while (SYM.sym == SCAN_comma)
{ GetSym(); OneActual(followers, procentry, actual); }
accept(SCAN_rparen);
}
if (actual != procentry.p.params)
Report->error(209); // wrong number of arguments
}
void PARSER::OneActual(TABLE_entries procentry, int &actual)
// OneActual = ArrayIdentifier | Expression . (depends on context)
{ actual++; // one more argument
if (Table->isrefparam(procentry, actual)) // check symbol table
ReferenceParameter();
else
Expression();
}
The several situations where it is necessary to generate code that will push the run-time address of a variable or
parameter onto the stack all depend ultimately on the stackaddress routine in the code generator interface. This
has to be more complex than before, because in the situations where a variable is really an alias for a parameter
that has been passed by reference, the offset recorded in the symbol table is really the offset where one will find
yet another address. To push the true address onto the stack requires that we load the address of the offset, and
then dereference this to find the address that we really want. Hence the code generation interface takes the form
stackaddress(int level, int offset, bool byref);
which, for our stack machine will emit a LDA level offset instruction, followed by a VAL instruction if byref is
true. This has an immediate effect on the parser for a Designator, which now becomes:
void PARSER::Designator(TABLE_entries entry)
// Designator = VarIdentifier [ "[" Expression "]" ] .
{ CGen->stackaddress(entry.level, entry.v.offset, entry.v.ref); // base address
GetSym();
if (SYM.sym == SCAN_lbracket) // array reference
{ GetSym();
Expression(); // code to evaluate index
if (entry.v.ref) // get size from hidden parameter
CGen->stackaddress(entry.level, entry.v.offset + 1, entry.v.ref);
else // size known from symbol table
CGen->stackconstant(entry.v.size);
CGen->subscript();
accept(SCAN_rbracket);
}
}
The first call to stackaddress is responsible for generating code to push the address of a scalar variable onto the
stack, or the address of the first element of an array. If this array has been passed by reference it is necessary to
dereference that address to find the true address of the first element of the array, and to determine the true size of
the array by retrieving the next (hidden) actual parameter. Another situation in which we wish to push such
addresses onto the stack arises when we wish to pass a formal array parameter on to another routine as an actual
parameter. In this case we have to push not only the address of the base of the array, but also a second hidden
argument that specifies its size. This is handled by the parser that deals with a ReferenceParameter:
void PARSER::ReferenceParameter(void)
// ReferenceParameter = ArrayIdentifier . (unsubscripted)
{ TABLE_entries entry;
Table->search(SYM.name, entry); // assert : SYM.sym = identifier
CGen->stackaddress(entry.level, entry.v.offset, entry.v.ref); // base
// pass size as next parameter
if (entry.v.ref) // get size from formal parameter
CGen->stackaddress(entry.level, entry.v.offset + 1, entry.v.ref);
else // size known from symbol table
CGen->stackconstant(entry.v.size);
GetSym(); // should be comma or rparen
}
The variations on the ReturnStatement are easily checked, since we have already made provision for each Block to
be aware of its category. Within a function a ReturnStatement is really an assignment statement, with a
destination whose address is always at an offset of 1 from the base of the stack frame.
void PARSER::ReturnStatement(void)
// ReturnStatement = "RETURN" [ Expression ] .
{ GetSym(); // accept RETURN
switch (blockclass) // semantics depend on context
{ case TABLE_funcs:
CGen->stackaddress(blocklevel, 1, false); // address of return value
Expression(followers); CGen->assign(); // code to compute and assign
CGen->leavefunction(blocklevel); break; // code to exit function
case TABLE_procs:
CGen->leaveprocedure(blocklevel); break; // direct exit from procedure
case TABLE_progs:
CGen->leaveprogram(); break; // direct halt from main program
}
}
As illustrative examples we give the code for the programs discussed previously:
0 : PROGRAM Debug;
0 :
0 : FUNCTION Factorial (M);
2 : BEGIN
2 : IF M <= 1 THEN RETURN 1;
20 : RETURN M * Factorial(M-1);
43 : END;
44 :
44 : VAR N;
44 :
44 : BEGIN
46 : READ(N);
50 : WHILE N > 0 DO
59 : BEGIN WRITE(Factorial(N)); READ(N) END;
75 : END.
0 BRN 44 Jump to start of program 40 RET 2 1 Exit function
2 ADR 2 -5 BEGIN Factorial 43 NFN END Factorial
5 VAL Value of M 44 DSP 1 BEGIN main program
6 LIT 1 46 ADR 1 -1 Address of N
8 LEQ M <= 1 ? 49 INN READ(N)
9 BZE 20 IF M <= 1 THEN 50 ADR 1 -1 Address of N
11 ADR 2 -1 Address of return val 53 VAL Value of N
14 LIT 1 Value of 1 54 LIT 0 WHILE N > 0 DO
16 STO Store as return value 56 GTR
17 RET 2 1 Exit function 57 BZE 75
20 ADR 2 -1 Address of return value 59 MST Mark stack
23 ADR 2 -5 Address of M 60 ADR 1 -1 Address of N
26 VAL Value of M 63 VAL Value of N (argument)
27 MST Mark stack 64 CAL 1 2 Call Factorial
28 ADR 2 -5 Address of M 67 PRN WRITE(result)
31 VAL Value of M 68 NLN
32 LIT 1 69 ADR 1 -1
34 SUB Value of M-1 (argument) 72 INN READ(N)
35 CAL 1 2 Recursive call 73 BRN 50 END
38 MUL Value M*Factorial(M-1) 75 HLT END
39 STO Store as return value
0 : PROGRAM Debug;
2 :
2 : FUNCTION Last (List[], Limit);
2 : BEGIN
2 : RETURN List[Limit];
23 : END;
24 :
24 : PROCEDURE Analyze (Data[], N);
24 : VAR
26 : LocalData[2];
26 : BEGIN
26 : Write(Last(Data, N+2), Last(LocalData, 1));
59 : END;
62 :
62 : VAR
62 : GlobalData[3];
62 :
62 : BEGIN
64 : Analyze(GlobalData, 1);
75 : END.
0 BRN 62 Jump to start of program 38 VAL Value of N
2 ADR 2 -1 Address of return value 39 LIT 2
5 ADR 2 -5 41 ADD Value of N+2 (argument)
8 VAL Address of List[0] 42 CAL 1 2 Last(Data, N+2)
9 ADR 2 -7 Address of Limit 45 PRN Write result
12 VAL Value of Limit 46 MST Mark Stack
13 ADR 2 -6 47 ADR 2 -8 Address of LocalData[0]
16 VAL Size of List 50 LIT 3 Size of LocalData
17 IND Subscript 52 LIT 1 Value 1 (parameter)
18 VAL Value of List[Limit] 54 CAL 1 2 Last(LocalData, 1)
19 STO Store as return value 57 PRN Write result
20 RET 2 1 and exit function 58 NLN WriteLn
23 NFN END Last 59 RET 2 0 END Analyze
24 DSP 3 BEGIN Analyze 62 DSP 4 BEGIN Debug
26 MST Mark Stack 64 MST Mark stack
27 ADR 2 -5 First argument is 65 ADR 1 -1 Address of GlobalData[0]
30 VAL Address of Data[0] 68 LIT 4 Size of GlobalData
31 ADR 2 -6 Hidden argument is 70 LIT 1 Value 1 (argument)
34 VAL Size of Data 72 CAL 1 24 Analyze(GlobalData, 1)
35 ADR 2 -7 Compute last argument 75 HLT END
17.6.2 Semantic analysis and code generation in a Coco/R generated compiler
If we wish to write an LL(1) grammar as input for Coco/R, things become somewhat more complex. We are
obliged to write our productions as
Statement = AssignmentOrCall | ...
AssignmentOrCall = Designator ( ":=" Expression | ActualParameters ) .
ActualParameters = [ "(" OneActual { "," OneActual } ")" ] .
OneActual = Expression .
Factor = Designator ActualParameters | number
| "(" Expression ")" .
Designator = identifier [ "[" Expression "]" ] .
ReturnStatement = "RETURN" [ Expression ] .
This implies that Designator and Expression have to be attributed rather cleverly to allow all the conflicts to be
resolved. This can be done in several ways. We have chosen to illustrate a method where the routines
responsible for parsing these productions are passed a Boolean parameter stipulating whether they are being called
in a context that requires that the appearance of an array name must be followed by a subscript (this is always the
case except where an actual parameter is syntactically an expression, but must semantically be an unsubscripted
array name). On its own this system is still inadequate for constraint analysis, and we must also provide some
method for checking whether an expression used as an actual reference parameter is comprised only of an
unsubscripted array name.
At the same time we may take the opportunity to discuss the use of an AST as an intermediate representation of
the semantic structure of a program, by extending the treatment found in section 15.3.2. The various node classes
introduced in that section are extended and enhanced to support the idea of a node to represent a procedure or
function call, linked to a set of nodes each of which represents an actual parameter, and each of which, in turn, is
linked to the tree structure that represents the expression associated with that actual parameter. The sort of
structures we set up are exemplified in Figure 17.5, which depicts an AST corresponding to the procedure call in
the program outlined below
PROGRAM Debug;
FUNCTION F (X);
BEGIN END; (* body of F *)
PROCEDURE P (U, V[], W);
BEGIN END; (* body of P *)
VAR
X, Y, A[7];
BEGIN
P(F(X+5), A, Y)
END.
|
|
PROCNODE
entry P
lastparam ------------------------------------.
firstparam ---------. |
| |
PARAMNODE |
next ----------. |
.----- par | |
| | |
PROCNODE PARAMNODE |
entry F next ---------.|
.---------- lastparam .---- par ||
|.--------- firstparam | ||
|| | PARAMNODE
|| REFNODE next -------.
PARAMNODE offset A[0] par ----. |
.---- next size -----. | =
| par ------. | |
| | CONSTNODE VARNODE
= BINOPNODE value 8 offset Y
op +
.----- left
| right ----.
| |
VARNODE CONSTNODE
offset X value 5
Figure 17.5 AST structures for the statement P(F(X+5), A, Y )
Our base NODE class is extended slightly from the one introduced earlier, and now incorporates a member for
linking nodes together when they are elements of argument lists:
struct NODE {
int value; // value to be associated with this node
bool defined; // true if value predictable at compile time
bool refnode; // true if node corresponds to a ref parameter
NODE() { defined = false; refnode = false; }
virtual void emit1(void) = 0;
virtual void emit2(void) = 0;
virtual void link(AST next) = 0;
};
Similarly, the VARNODE class has members to record the static level, and whether the corresponding variable is a
variable in its own right, or is simply an alias for an array passed by reference:
struct VARNODE : public NODE {
bool ref; // direct or indirectly accessed
int level; // static level of declaration
int offset; // offset of variable assigned by compiler
VARNODE() {;} // default constructor
VARNODE(bool R, int L, int O) { ref = R; level = L; offset = O; }
virtual void emit1(void); // generate code to retrieve value of variable
virtual void emit2(void); // generate code to retrieve address of variable
virtual void link(AST next) {;}
};
Procedure and function calls give rise to instances of a PROCNODE class. Such nodes need to record the static level
and entry point of the routine, and have further links to the nodes that are set up to represent the queue of actual
parameters or arguments. It is convenient to introduce two such pointers so as to simplify the link member
function that is responsible for building this queue.
struct PROCNODE : public NODE {
int level, entrypoint; // static level, address of first instruction
AST firstparam, lastparam; // pointers to argument list
PROCNODE(int L, int E)
{ level = L; entrypoint = E; firstparam = NULL; lastparam = NULL; }
virtual void emit1(void); // generate code for procedure/function call
virtual void emit2(void) {;}
virtual void link(AST next); // link next actual parameter
};
The actual arguments give rise to nodes of a new PARAMNODE class. As can be seen from Figure 17.5, these require
pointer members: one to allow the argument to be linked to another argument, and one to point to the expression
tree for the argument itself:
struct PARAMNODE : public NODE {
AST par, next; // pointers to argument and to next argument
PARAMNODE(AST P) { par = P; next = NULL; }
virtual void emit1(void); // push actual parameter onto stack
virtual void emit2(void) {;}
virtual void link(AST param) { next = param; }
};
Actual parameters are syntactically expressions, but we need a further REFNODE class to handle the passing of arrays
as actual parameters:
struct REFNODE : public VARNODE {
AST size; // real size of array argument
REFNODE(bool R, int L, int O, AST S)
{ ref = R; level = L; offset = O; size = S; refnode = true; }
virtual void emit1(void); // generate code to push array address, size
virtual void emit2(void) {;}
virtual void link(AST next) {;}
};
Tree building operations may be understood by referring to the attributes with which a Cocol specification would
be decorated:
AssignmentOrCall
= (. TABLE_entries entry; AST des, exp;.)
Designator<des, classset(TABLE_vars, TABLE_procs), entry, true>
( /* assignment */ (. if (entry.idclass != TABLE_vars) SemError(210); .)
":=" Expression<exp, true>
SYNC (. CGen->assign(des, exp); .)
| /* procedure call */ (. if (entry.idclass < TABLE_procs)
{ SemError(210); return; }
CGen->markstack(des, entry.level,
entry.p.entrypoint); .)
ActualParameters<des, entry>
(. CGen->call(des); .)
) .
Designator<AST &D, classset allowed, TABLE_entries &entry, bool entire>
= (. TABLE_alfa name; AST index, size;
bool found;
D = CGen->emptyast(); .)
Ident<name> (. Table->search(name, entry, found);
if (!found) SemError(202);
if (!allowed.memb(entry.idclass)) SemError(206);
if (entry.idclass != TABLE_vars) return;
CGen->stackaddress(D, entry.level,
entry.v.offset, entry.v.ref); .)
( "[" (. if (entry.v.scalar) SemError(204); .)
Expression<index, true>
(. if (!entry.v.scalar)
/* determine size for bounds check */
{ if (entry.v.ref)
CGen->stackaddress(size, entry.level,
entry.v.offset + 1, false);
else
CGen->stackconstant(size, entry.v.size);
CGen->subscript(D, entry.v.ref, entry.level,
entry.v.offset, size, index);
} .)
"]"
| (. if (!entry.v.scalar)
{ if (entire) SemError(205);
if (entry.v.ref)
CGen->stackaddress(size, entry.level,
entry.v.offset + 1, false);
else
CGen->stackconstant(size, entry.v.size);
CGen->stackreference(D, entry.v.ref, entry.level,
entry.v.offset, size);
} .)
) .
ActualParameters<AST &p, TABLE_entries proc>
= (. int actual = 0; .)
[ "(" (. actual++; .)
OneActual<p, (*Table).isrefparam(proc, actual)>
{ WEAK "," (. actual++; .)
OneActual<p, (*Table).isrefparam(proc, actual)> } ")"
] (. if (actual != proc.p.params) SemError(209); .) .
OneActual<AST &p, bool byref>
= (. AST par; .)
Expression<par, !byref> (. if (byref && !CGen->isrefast(par)) SemError(214);
CGen->linkparameter(p, par); .) .
ReturnStatement
= (. AST dest, exp; .)
"RETURN"
( (. if (blockclass != TABLE_funcs) SemError(219);
CGen->stackaddress(dest, blocklevel, 1, false); .)
Expression<exp, true>
(. CGen->assign(dest, exp);
CGen->leavefunction(blocklevel); .)
| /* empty */ (. switch (blockclass)
{ case TABLE_procs :
CGen->leaveprocedure(blocklevel); break;
case TABLE_progs :
CGen->leaveprogram(); break;
case TABLE_funcs :
SemError(220); break;
} .)
) .
Expression<AST &E, bool entire>
= (. AST T; CGEN_operators op;
E = CGen->emptyast(); .)
( "+" Term<E, true>
| "-" Term<E, true> (. CGen->negateinteger(E); .)
| Term<E, entire>
)
{ AddOp<op> Term<T, true>(. CGen->binaryintegerop(op, E, T); .)
} .
Term<AST &T, bool entire>
= (. AST F; CGEN_operators op; .)
Factor<T, entire>
{ ( MulOp<op>
| /* missing op */ (. SynError(92); op = CGEN_opmul; .)
) Factor<F, true> (. CGen->binaryintegerop(op, T, F); .)
} .
Factor<AST &F, bool entire>
= (. TABLE_entries entry;
int value;
F = CGen->emptyast(); .)
Designator<F, classset(TABLE_consts, TABLE_vars, TABLE_funcs), entry, entire>
(. switch (entry.idclass)
{ case TABLE_consts :
CGen->stackconstant(F, entry.c.value); return;
case TABLE_procs :
case TABLE_funcs :
CGen->markstack(F, entry.level,
entry.p.entrypoint); break;
case TABLE_vars :
case TABLE_progs :
return;
} .)
ActualParameters<F, entry>
| Number<value> (. CGen->stackconstant(F, value); .)
| "(" Expression<F, true> ")" .
The reader should compare this with the simpler attributed grammar presented in section 15.3.2, and take note of
the following points:
- All productions that have to deal with identifiers call upon Designator. So far as code generation is
concerned, this production is responsible for creating nodes that represent the addresses of variables. Where
other identifiers are recognized, execution of a return bypasses code generation, and leaves the routine after
retrieving the symbol table entry for that identifier.
- Designator must now permit the appearance of an unsubscripted array name, creating an instance of a REFNODE
in this case. Note the use of the entire parameter passed to Designator, Expression, Term and Factor to
enable checking of the context in which the subscript may be omitted.
- Parsing of OneActual is simply effected by a call to Expression. After this parsing is completed, a check must
be carried out to see whether a reference parameter does, in fact, consist only of an unsubscripted array name.
Notice that OneActual also incorporates a call to a new code generating routine that will link the node just
created for the actual parameter to the parameter list emanating from the node for the procedure itself, a node
that was created by the markstack routine.
- Productions like AssignmentOrCall and Factor follow the call to Designator with tests on the class of the
identifier that has been recognized, and use this information to drive the parse further (in Factor) or to check
constraints (in AssignmentOrCall).
As before, once a AST structure has been built, it can be traversed and the corresponding code generated by virtue
of each node "knowing" how to generate its own code. It will suffice to demonstrate two examples. To generate
code for a procedure call for our hypothetical stack machine we define the emit1 member function to be
void PROCNODE::emit1(void)
// generate procedure/function activation and call
{ CGen->emit(int(STKMC_mst));
if (firstparam) { firstparam->emit1(); delete firstparam; }
CGen->emit(int(STKMC_cal));
CGen->emit(level);
CGen->emit(entrypoint);
}
which, naturally, calls on the emit1 member of its first parameter to initiate the stacking of the actual parameters
as part of the activation sequence. This member, in turn, calls on the emit1 member of its successor to handle
subsequent arguments:
void PARAMNODE::emit1(void)
// push actual parameter onto stack during activation
{ if (par) { par->emit1(); delete par; } // push this argument
if (next) { next->emit1(); delete next; } // follow link to next argument
}
Source code for the complete implementation of the code generator class can be found in Appendix C and also on
the source diskette, along with implementations for hand-crafted compilers that make use of tree structures, and
implementations that make use of the traditional variant records or unions to handle the inhomogeneity of the tree
nodes.
Exercises
17.1 Some authors suggest that value-returning function subprograms are not really necessary; one can
simply use procedures with call-by-reference parameter passing instead. On the other hand, in C++ all
subprograms are potentially functions. Examine the relative merits of providing both in a language,
from the compiler writer's and the user's viewpoints.
17.2 Extend Topsy and its compiler to allow functions and procedures to have parameters. Can you do this
in such a way a function can be called either as an operand in an expression, or as a stand-alone
statement, as in C++?
17.3 The usual explanation of call-by-value leaves one with the impression that this mode of passing is very
safe, in that changes within a subprogram can be confined to that subprogram. However, if the value
of a pointer variable is passed by value this is not quite the whole story. C does not provide call-by-
reference, because the same effect can be obtained by writing code like
void swap (int *x, int *y)
{ int z; z = *x; *x = *y; *y = z; }
Extend Topsy to provide explicit operators for computing an address, and dereferencing an address (as
exemplified by &variable and *variable in C), and use these features to provide a reference passing
mechanism for scalar variables. Is it possible to make these operations secure (that is, so that they
cannot be abused)? Are any difficulties caused by overloading the asterisk to mean multiplication in
one context and dereferencing an address in another context?
17.4 The array passing mechanisms we have devised effectively provide the equivalent of Modula-2's "open"
array mechanism for arrays passed by reference. Extend Clang and its implementation to provide the
equivalent of the HIGH function to complete the analogy.
17.5 Implement parameter passing in Clang in another way - use the Pascal/Modula convention of preceding
formal parameters by the keyword VAR if the call-by-reference mechanism is to be used. Pay particular
attention to the problems of array parameters.
17.6 In Modula-2 and Pascal, the keyword VAR is used to denote call-by-reference, but no keyword is used
for the (default) call-by-value. Why does this come in for criticism? Is the word VAR a good choice?
17.7 How do you cater for forward declaration of functions and procedures when you have to take
formal parameters into account (see Exercise 16.17)?
17.8 (Longer) If you extend Clang or Topsy to introduce a Boolean type as well as an integer one (see
Exercise 14.30), how do you solve the host of interesting problems that arise when you wish to
introduce Boolean functions and Boolean parameters?
17.9 Follow up the suggestion that parameters can be evaluated before the frame header is allocated, and are
then accessed through positive offsets from the base register BP.
17.10 Exercise 15.16 suggested the possibility of peephole optimization for replacing the common code
sequence for loading an address and then dereferencing this, assuming the existence of a more powerful
STKMC_psh operation. How would this be implemented when procedures, functions, arrays and
parameters are involved?
17.11 In previous exercises we have suggested that undeclared identifiers could be entered into the symbol
table at the point of first declaration, so as to help with suppressing further spurious errors. What is
the best way of doing this if we might have undeclared variables, arrays, functions, or procedures?
17.12 (Harder) Many languages allow formal parameters to be of a procedure type, so that procedures or
functions may be passed as actual parameters to other routines. C++ allows the same effect to be
achieved by declaring formal parameters as pointers to functions. Can you extend Clang or Topsy to
support this feature? Be careful, for the problem might be more difficult than it looks, except for some
special simple cases.
17.13 Introduce a few standard functions and procedures into your languages, such as the ABS, ODD and CHR of
Modula-2. Although it is easier to define these names to be reserved keywords, introduce them as
pervasive (predeclared) identifiers, thus allowing them to be redeclared at the user's whim.
17.14 It might be thought that the constraint analysis on actual parameters in the Cocol grammar could be
simplified so as to depend only on the entire parameter passed to the various parsing routines, without
the need for a check to be carried out after an Expression had been parsed. Why is this check needed?
17.15 If you study the interpreter that we have been developing, you should be struck by the fact that this
does a great deal of checking that the stack pointer stays within bounds. This check is strictly
necessary, although unlikely to fail if the memory is large enough. It would probably suffice to
check only for opcodes that push a value or address onto the stack. Even this would severely degrade
the efficiency of the interpreter. Suggest how the compiler and run-time system could be modified so
that at compile-time a prediction is made of the extra depth needed by the run-time stack by each
procedure. This will enable the run-time system to do a single check that this limit will not be
exceeded, as the procedure or program begins execution. (A system on these lines is suggested by
Brinch Hansen (1985)).
17.16 Explore the possibility of providing a fairly sophisticated post-mortem dump in the extended
interpreter. For example, provide a trace of the subprogram calls up to the point where an error was
detected, and give the values of the local variables in each stack frame. To be really user-friendly the
run-time system will need to refer to the user names for such entities. How would this alter the whole
implementation of the symbol table?
17.17 Now that you have a better understanding of how recursion is implemented, study the compiler you are
writing with new interest. It uses recursion a great deal. How deeply do you suppose this recursion
goes when the compiler executes? Is recursive descent "efficient" for all aspects of the compiling
process? Do you suppose a compiler would ever run out of space in which to allocate new stack frames
for itself when it was compiling large programs?
Further reading
As already mentioned, most texts on recursive descent compilers for block-structured languages treat the material
of the last few sections in fair detail, discussing one or other approach to stack frame allocation and management.
You might like to consult the texts by Fischer and LeBlanc (1988, 1991), Watson (1989), Elder (1994) or Wirth
(1996). The special problem of procedural parameters is discussed in the texts by Aho, Sethi and Ullman (1986)
and Fischer and LeBlanc (1988, 1991). Gough and Mohay (1988) discuss the related problem of procedure
variables as found in Modula-2.
17.7 Language design issues
In this section we wish to explore a few of the many language design issues that arise when one introduces the
procedure and function concepts.
17.7.1 Scope rules
Although the scope rules we have discussed probably seem sensible enough, it may be of interest to record that
the scope rules in Pascal originally came in for extensive criticism, as they were incompletely formulated, and led
to misconceptions and misinterpretation, especially when handled by one-pass systems. Most of the examples
cited in the literature have to do with the problems associated with types, but we can give an example more in
keeping with our own language to illustrate a typical difficulty. Suppose a compiler were to be presented with the
following:
PROGRAM One;
PROCEDURE Two (* first declared here *);
BEGIN
WRITE('First Two')
END (* Two *);
PROCEDURE Three;
PROCEDURE Four;
BEGIN
Two
END (* Four *);
PROCEDURE Two (* then redeclared here *);
BEGIN
WRITE('Second Two')
END (* Two *);
BEGIN
Four; Two
END (* Three *);
BEGIN
Three
END (* One *).
At the instant where procedure Four is being parsed, and where the call to Two is encountered, the first procedure
Two (in the symbol table at level 1) seems to be in scope, and code will presumably be generated for a call to this.
However, perhaps the second procedure Two should be the one that is in scope for procedure Four; one
interpretation of the scope rules would require code to be generated for a call to this. In a one-pass system this
would be a little tricky, as this second procedure Two would not yet have been encountered by the compiler - but
note that it would have been by the time the calls to Four and Two were made from procedure Three.
This problem can be resolved to the satisfaction of a compiler writer if the scope rules are formulated so that the
scope of an identifier extends from the point of its declaration to the end of the block in which it is declared, and
not over the whole block in which it is declared. This makes for easy one-pass compilation, but it is doubtful
whether this solution would please a programmer who writes code such as the above, and falls foul of the rules
without the compiler reporting the fact.
An ingenious way for a single-pass compiler to check that the scope of an identifier extends over the whole of the
block in which it has been declared was suggested by Sale (1979). The basic algorithm requires that every block
be numbered sequentially as it compiled (notice that these numbers do not represent nesting levels). Each
identifier node inserted into the symbol table has an extra numeric attribute. This is originally defined to be the
unique number of the block making the insertion, but each time that the identifier is referenced thereafter, this
attribute is reset to the number of the block making the reference. Each time an identifier is declared, and needs
to be entered into the table, a search is made of all the identifiers that are in scope to see if a duplicate identifier
entry can be found that is already attributed with a number equal to or greater than that of the block making the
declaration. If this search succeeds, it implies that the scope rules are about to be violated. This simple scheme
has to be modified, of course, if the language allows for legitimate forward declarations and function prototypes.
17.7.2 Function return mechanisms
Although the use of an explicit ReturnStatement will seem natural to a programmer familiar with Modula-2 or
C++, it is not the only device that has been explored by language designers. In Pascal, for example, the value to
be returned must be defined by means of what appears to be an assignment to a variable that has the same name as
the function. Taken in conjunction with the fact that in Pascal a parameterless function call also looks like a
variable access, this presents numerous small difficulties to a compiler writer, as a study of the following example
will reveal
PROGRAM Debug;
VAR B, C;
FUNCTION One (W);
VAR X, Y;
FUNCTION Two (Z);
FUNCTION Three;
BEGIN
Two := B + X; (* should this be allowed ? *)
Three := Three; (* syntactically correct, although useless *)
END;
BEGIN
Two := B + Two(4); (* must be allowed *)
Two := B + X; (* must be allowed *)
Two := Three; (* must be allowed *)
Three := 4; (* Three is in scope, but cannot be used like this *)
END;
BEGIN
Two := B + X; (* Two is in scope, but cannot be used like this *)
X := Two(Y); (* must be allowed *)
END;
BEGIN
One(B)
END.
Small wonder that in his later language designs Wirth adopted the explicit return statement. Of course, even this
does not find favour with some structured language purists, who preach that each routine should have exactly one
entry point and exactly one exit point.
Exercises
17.18 Submit a program similar to the example in section 17.7.1 to any compilers you may be using, and
detect which interpretation they place on the code.
17.19 Implement the Sale algorithm in your extended Clang compiler. Can the same sort of scope conflicts
arise in C++, and if so, can you find a way to ensure that the scope of an identifier extends over the
whole of the block in which it is declared, rather than just from the point of declaration onwards?
17.20 The following program highlights some further problems with interpreting the scope rules of languages
when function return values are defined by assignment statements.
PROGRAM Silly;
FUNCTION F;
FUNCTION F (F) (* nested, and same parameter name as function *);
BEGIN
F := 1
END (* inner F *);
BEGIN (* outer F *)
F := 2
END (* outer F *);
BEGIN
WRITE(F)
END (* Silly *).
What would cause problems in one-pass (or any) compilation, and what could a compiler writer do
about solving these?
17.21 Notwithstanding our comments on the difficulties of using an assignment statement to specify the value
to be returned from a function, develop a version of the Clang compiler that incorporates this idea.
17.22 In Modula-2, a procedure declaration requires the name of the procedure to be quoted again after the
terminating END. Of what practical benefit is this?
17.23 In classic Pascal the ordering of the components in a program or procedure block is very restrictive. It
may be summarized in EBNF on the lines of
Block = [ ConstDeclarations ]
[ TypeDeclarations ]
[ VarDeclarations ]
{ ProcDeclaration }
CompoundStatement .
In Modula-2, however, this ordering is highly permissive:
Block = { ConstDeclarations | TypeDeclarations | VarDeclarations | ProcDeclaration }
CompoundStatement .
Oberon (Wirth, 1988b) introduced an interesting restriction:
Block = { ConstDeclarations | TypeDeclarations | VarDeclarations }
{ ProcDeclaration }
CompoundStatement .
Umbriel (Terry, 1995) imposes a different restriction:
Block = { ConstDeclarations | TypeDeclarations | ProcDeclaration }
{ VarDeclarations }
CompoundStatement .
Although allowing declarations to appear in any order makes for the simplest grammar, languages that
insist on a specific order presumably do so for good reasons. Can you think what these might be?
17.24 How would you write a Cocol grammar or a hand-crafted parser to insist on a particular declaration
order, and yet recover satisfactorily if declarations were presented in any order?
17.25 Originally, in Pascal a function could only return a scalar value, and not, for example, an ARRAY, RECORD
or SET. Why do you suppose this annoying restriction was introduced? Is there any easy (legal) way
around the problem?
17.26 Several language designers decry function subprograms for the reason that most languages do not
prevent a programmer from writing functions that have side-effects. The program below illustrates
several esoteric side-effects. Given that one really wishes to prevent these, to what extent can a
compiler detect them?
PROGRAM Debug;
VAR
A, B[12];
PROCEDURE P1 (X[]);
BEGIN
X[3] := 1 (* X is passed by reference *)
END;
PROCEDURE P2;
BEGIN
A := 1 (* modifies global variable *)
END;
PROCEDURE P3;
BEGIN
P2 (* indirect attack on a global variable *)
END;
PROCEDURE P4;
VAR C;
FUNCTION F (Y[]);
BEGIN
A := 3 (* side-effect *);
C := 4 (* side-effect *);
READ(A) (* side-effect *);
Y[4] := 4 (* side-effect *);
P1(B) (* side-effect *);
P2 (* side-effect *);
P3 (* side-effect *);
P4 (* side-effect *);
RETURN 51
END;
BEGIN
A := F(B);
END;
BEGIN
P4
END.
17.27 If you introduce a FOR loop into Clang (see Exercise 14.46), how could you prevent a malevolent
program from altering the value of the loop control variable within the loop? Some attempts are easily
detected, but those involving procedure calls are a little trickier, as study of the following might reveal:
PROGRAM Threaten;
VAR i;
PROCEDURE Nasty (VAR x);
BEGIN
x := 10
END;
PROCEDURE Nastier;
BEGIN
i := 10
END;
BEGIN
FOR i := 0 TO 10 DO
FOR i := 0 TO 5 DO (* Corrupt by using as inner control variable *)
BEGIN
READ(i) (* Corrupt by reading a new value *);
i := 6 (* Corrupt by direct assignment *);
Nasty(i) (* Corrupt by passing i by reference *);
Nastier (* Corrupt by calling a procedure having i in scope *)
END
END.
Further reading
Criticisms of well established languages like Pascal, Modula-2 and C are worth following up. The reader is
directed to the classic papers by Welsh, Sneeringer and Hoare (1977) (reprinted in Barron (1981)), Kernighan
(1981), Cailliau (1982), Cornelius (1988), Mody (1991), and Sakkinen (1992) for evidence that language design
is something that does not always please users.
Contents (GIF version) | Contents (Symbol Font version) | Home © P.D. Terry
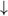 `---------------. = | | | `-->.--------.
.-----. .------. .------. .------. .-----.`---->| |
|First|---->| G1 |->| One |->| Two |->|Three|----->| |-.
|-----| `------' `------' `------' `-----' .-->`--------' |
|Down | | =
`-----' |
`---------------. = | | | `-->.--------.
.-----. .------. .------. .------. .-----.`---->| |
|First|---->| G1 |->| One |->| Two |->|Three|----->| |-.
|-----| `------' `------' `------' `-----' .-->`--------' |
|Down | | =
`-----' |
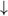 |
.-----. .------. |
|First|---->| Main |-------------------------------'
|-----| `------'
|Down |
`-----'
=
Figure 17.1 A symbol table structure with links from procedure entries to formal parameter entries
|
.-----. .------. |
|First|---->| Main |-------------------------------'
|-----| `------'
|Down |
`-----'
=
Figure 17.1 A symbol table structure with links from procedure entries to formal parameter entries
 SP
SP