 Data Structures and Algorithms
with Object-Oriented Design Patterns in C++
Data Structures and Algorithms
with Object-Oriented Design Patterns in C++

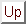



Consider a tree T containing the set of nodes R
as given by Definition  .
.
-
The level
or depth of a node
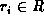 in a tree T is the length of the unique path in T
from its root r to the node
in a tree T is the length of the unique path in T
from its root r to the node 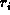 .
E.g., the root of T is at level zero and
the roots of the subtrees are of T are at level one.
.
E.g., the root of T is at level zero and
the roots of the subtrees are of T are at level one. -
The height of a node
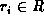 in a tree T
is the length of the longest path from node
in a tree T
is the length of the longest path from node 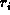 to a leaf.
Therefore, the leaves are all at height zero.
to a leaf.
Therefore, the leaves are all at height zero. -
The height of a tree
T is the height of its root node r.
-
Consider two nodes
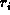 and
and 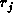 in a tree T.
The node
in a tree T.
The node 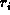 is an ancestor
of the node
is an ancestor
of the node 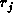 if there exists a path in T from
if there exists a path in T from 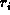 to
to 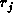 .
Notice that
.
Notice that 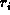 and
and 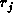 may be the same node.
I.e., a node is its own ancestor.
However, the node
may be the same node.
I.e., a node is its own ancestor.
However, the node 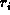 is a proper ancestor
if there exists a path p in T from
is a proper ancestor
if there exists a path p in T from 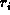 to
to 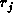 such that the length of the path p is non-zero.
such that the length of the path p is non-zero. -
Similarly, node
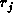 is a descendant
of the node
is a descendant
of the node 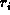 if there exists a path in T from
if there exists a path in T from 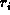 to
to 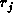 .
And since
.
And since 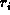 and
and 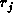 may be the same node,
a node is its own descendant.
The node
may be the same node,
a node is its own descendant.
The node 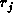 is a proper descendant
if there exists a path p in T from
is a proper descendant
if there exists a path p in T from 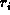 to
to 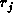 such that the length of the path p is non-zero.
such that the length of the path p is non-zero.




 Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.
Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.
![]() .
.