 Data Structures and Algorithms
with Object-Oriented Design Patterns in C++
Data Structures and Algorithms
with Object-Oriented Design Patterns in C++




The Graph class declares the following
accessor and mutator member functions:
- NumberOfEdges
-
This accessor returns the number of edges contained by the graph.
- NumberOfVertices
-
This accessor returns the number of vertices contained by the graph.
- AddVertex
-
This mutator inserts a given vertex into a graph.
For simplicity, we shall assume that a given vertex
is inserted into exactly one graph.
All the vertices contained in a given graph must have
a unique vertex number.
Furthermore, if a graph contains n vertices,
those vertices shall be numbered 0, 1, ..., n-1.
Therefore, the next vertex inserted into the graph shall
have the number n.
- SelectVertex
-
This accessor takes an integer, say i where
 ,
and returns reference to the
,
and returns reference to the 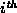 vertex
contained in the graph.
vertex
contained in the graph.
- operator[]
-
This subscript operator takes an integer-valued subscript expression.
We shall assume that the default behavior of this operator
is to call SelectVertex.
- AddEdge
-
This mutator inserts a given edge into a graph.
For simplicity, we shall assume that a given edge
is inserted into exactly one graph.
Both vertices referenced by the edge must be vertices
in the given graph.
- IsEdge
-
This Boolean-valued accessor takes two Vertex::Number arguments.
It returns true if the graph contains an edge
that connects the corresponding vertices.
- SelectEdge
-
This accessor takes two Vertex::Number arguments.
It returns a reference to the edge instance (if it exists)
that connects the corresponding vertices.
The behavior of this routine is undefined when the edge
does not exist.
(An implementation will typically throw an exception).
- IsCyclic
-
This Boolean-valued accessor returns true
if the graph is cyclic.
- IsConnected
-
This Boolean-valued accessor returns true
if the graph is connected.
Connectedness of graphs is discussed in Section
 .
.




 Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.
Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.