Exercises

Exercises

Merging two lists

Write a function merge_i which takes as input two integer lists sorted in increasing order and returns a new sorted list containing the elements of the first two.
```
# let rec merge_i l1 l2 = match (l1,l2) with
   [],_ -> l2
 | _,[] -> l1
 | h1::t1,h2::t2 ->
     if h1 < h2 then h1::(merge_i t1 l2) 
     else h2::(merge_i l1 t2);;
val merge_i : 'a list -> 'a list -> 'a list = <fun>
```
Write a general function merge which takes as argument a comparison function and two lists sorted in this order and returns the list merged in the same order. The comparison function will be of type 'a -> 'a -> bool.
```
# let rec merge ord_fn l1 l2 = match (l1,l2) with
   [],_ -> l2
 | _,[] -> l1
 | h1::t1,h2::t2 ->
     if ord_fn h1 h2 then h1::(merge ord_fn t1 l2) 
     else h2::(merge ord_fn l1 t2);;
val merge : ('a -> 'a -> bool) -> 'a list -> 'a list -> 'a list = <fun>
```
Apply this function to two integer lists sorted in decreasing order, then to two string lists sorted in decreasing order.
```
# merge (>) [44;33;22;11] [55;30;10];;
- : int list = [55; 44; 33; 30; 22; 11; 10]
# merge (>) ["my"; "first"; "effort"] 
            ["wonderful";"try";"number";"1"];;
- : string list =
["wonderful"; "try"; "number"; "my"; "first"; "effort"; "1"]
```
What happens if one of the lists is not in the required decreasing order? If at least one of the lists is not in the given order, then the result probably won't be.
Write a new list type in the form of a record containing three fields: the conventional list, an order function and a boolean indicating whether the list is in that order.
```
# type 'a slist = {l: 'a list; ord_fn : 'a -> 'a -> bool; is_in_order : bool};;
type 'a slist = { l: 'a list; ord_fn: 'a -> 'a -> bool; is_in_order: bool }
```
Write the function insert which adds an element to a list of this type.

Write a function sort which insertion sorts the elements of a list.


# let insert e ls =
   let rec insert_rec e l = match l with 
     [] -> [e]
   | h::t -> if ls.ord_fn e h then e::l 
             else h::(insert_rec e t)
   in 
     if ls.is_in_order then {ls with l=insert_rec e ls.l}
     else {ls with l = e::ls.l};;
val insert : 'a -> 'a slist -> 'a slist = <fun>


# let sort ls = 
   if ls.is_in_order then ls
   else  List.fold_right insert ls.l {l=[]; ord_fn=ls.ord_fn; is_in_order=true};;
val sort : 'a slist -> 'a slist = <fun>

Write a new function merge for these lists.


# let rec merge_ls l1 l2 = 
   if l1.is_in_order then 
     if l2.is_in_order then {l = merge l1.ord_fn l1.l l2.l; ord_fn = l1.ord_fn; is_in_order = true}
     else List.fold_right insert l2.l l1
   else
     if l2.is_in_order then  merge_ls l2 l1
     else  merge_ls (sort l1) l2;;
val merge_ls : 'a slist -> 'a slist -> 'a slist = <fun>

Lexical trees

Lexical trees (or tries) are used for the representation of dictionaries.


# type lex_node = Letter of char * bool * lex_tree 
 and  lex_tree = lex_node  list;;
# type word = string;;

The boolean value in lex_node marks the end of a word when it equals true. In such a structure, the sequence of words ``fa, false, far, fare, fried, frieze'' is stored in the following way:

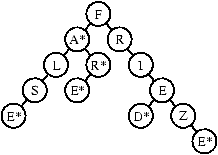
An asterisk (*) marks the end of a word.

Write the function exists which tests whether a word belongs to a dictionary of type lex_tree.


# let rec exists w d = 
   let aux sw i n = match d with
       [] -> false
     | (Letter (c,b,l))::t when c=sw.[i] -> 
          if n = 1 then b else exists (String.sub sw (i+1) (n-1)) l       
     | (Letter (c,b,l))::t -> exists sw t
   in aux w 0 (String.length w) ;;
val exists : string -> lex_tree -> bool = <fun>

Write a function insert which takes a word and a dictionary and returns a new dictionary which additionally contains this word. If the word is already in the dictionary, it is not necessary to insert it.


# let rec insert w d = 
   let aux sw i n = 
     if n = 0 then d 
     else match d with 
         [] -> [Letter (sw.[i], n = 1, insert (String.sub sw (i+1) (n-1)) [])]
       | (Letter(c,b,l))::t when c=sw.[i]-> 
            if n = 1 then (Letter(c,true,l))::t
            else Letter(c,b,insert (String.sub sw (i+1) (n-1)) l)::t
       | (Letter(c,b,l))::t -> (Letter(c,b,l))::(insert sw t)
   in aux w 0 (String.length w) ;;
val insert : string -> lex_tree -> lex_tree = <fun>

Write a function construct which takes a list of words and constructs the corresponding dictionary.
```
# let construct l = 
   let rec aux l d = match l with 
       [] -> d
     | h::t -> aux t (insert h d) 
   in aux l [] ;;
val construct : string list -> lex_tree = <fun>
```

Write a function verify which takes a list of words and a dictionary and returns the list of words not belonging to this dictionary.


# let rec filter p = function 
     [] -> []
   | h::t -> if p h then h::(filter p t) else filter p t ;;
val filter : ('a -> bool) -> 'a list -> 'a list = <fun>

# let verify l d = filter (function x -> not (exists x d)) l ;;
val verify : string list -> lex_tree -> string list = <fun>

Write a function select which takes a dictionary and a length and returns the set of words of this length.


# let string_of_char c = String.make 1 c ;;
val string_of_char : char -> string = <fun>
# let rec select n d = match d with 
     [] -> []
   | (Letter(c,b,l))::t when n=1 -> 
        let f (Letter (c,b,_)) = if b then string_of_char c else "!" in
        filter (function x -> x <> "!") (List.map f d)
   | (Letter(c,b,l))::t ->
          let r1 = select (n-1) l 
          and r2 = select n t in
          let pr = List.map (function s -> (string_of_char c)^s) r1 in
          pr@r2 ;;
val select : int -> lex_tree -> string list = <fun>

Graph traversal

We define a type 'a graph representing directed graphs by adjacency lists containing for each vertex the list of its successors:


# type 'a graph = ( 'a * 'a  list) list ;;

Write a function insert_vtx which inserts a vertex into a graph and returns the new graph.


# let rec insert_vtx v g = 
   match g with 
       [] -> [(v,[])]
     | (h,_)::_ when h=v -> failwith "existing vertex"
     | vl::t -> vl::(insert_vtx v t) ;;
val insert_vtx : 'a -> ('a * 'b list) list -> ('a * 'b list) list = <fun>

# let insert_vtx = (insert_vtx : 'a -> 'a graph -> 'a graph) ;;
val insert_vtx : 'a -> 'a graph -> 'a graph = <fun>

Write a function insert_edge which adds an edge to a graph already possessing these two vertices.


# let rec insert_edge v1 v2 g = 
   match g with 
       [] -> failwith "unknown vertex"
     | (h,el)::t when h=v1 -> 
         if List.mem v2 el then failwith "existing edge"
         else (v1,v2::el)::t
     | vl::t -> vl::(insert_edge v1 v2 t) ;; 
val insert_edge : 'a -> 'b -> ('a * 'b list) list -> ('a * 'b list) list =
  <fun>

# let insert_edge = (insert_edge : 'a -> 'a -> 'a graph -> 'a graph ) ;;
val insert_edge : 'a -> 'a -> 'a graph -> 'a graph = <fun>

Write a function has_edges_to which returns all the vertices following directly from a given vertex.


# let rec has_edges_to v g = match g with 
     [] -> []
   | (v',el)::_ when v=v' -> el
   | _::t -> has_edges_to v t ;; 
val has_edges_to : 'a -> ('a * 'b list) list -> 'b list = <fun>

# let has_edges_to = (has_edges_to : 'a -> 'a graph -> 'a list) ;;
val has_edges_to : 'a -> 'a graph -> 'a list = <fun>

Write a function has_edges_from which returns the list of all the vertices leading directly to a given vertex.


# let rec has_edges_from v g = match g with 
     [] -> []
   | (h,el)::t -> if List.mem v el then h::(has_edges_to v t)
                  else (has_edges_to v t) ;;
val has_edges_from : 'a -> ('a * 'a list) list -> 'a list = <fun>

# let has_edges_from = (has_edges_from : 'a -> 'a graph -> 'a list) ;;
val has_edges_from : 'a -> 'a graph -> 'a list = <fun>