This section summarizes and extends the above derivations in a more
formal manner (following portions of chapter 4 of
![]() ). In
particular, we establish that the sum of projections of
). In
particular, we establish that the sum of projections of
![]() onto
onto ![]() vectors
vectors
![]() will give back the original vector
will give back the original vector
![]() whenever the set
whenever the set
![]() is an orthogonal
basis for
is an orthogonal
basis for ![]() .
.
Definition: A set of vectors is said to form a vector space if, given
any two members ![]() and
and ![]() from the set, the vectors
from the set, the vectors
![]() and
and ![]() are also in the set, where
are also in the set, where
![]() is any
scalar.
is any
scalar.
Definition: The set of all ![]() -dimensional complex vectors is denoted
-dimensional complex vectors is denoted
![]() . That is,
. That is, ![]() consists of all vectors
consists of all vectors
![]() defined as a list of
defined as a list of ![]() complex numbers
complex numbers
![]() .
.
Theorem: ![]() is a vector space under elementwise addition and
multiplication by complex scalars.
is a vector space under elementwise addition and
multiplication by complex scalars.
Proof: This is a special case of the following more general theorem.
Theorem: Let ![]() be an integer greater than 0. Then the set of all
linear combinations of
be an integer greater than 0. Then the set of all
linear combinations of ![]() vectors from
vectors from ![]() forms a vector space
under elementwise addition and multiplication by complex scalars.
forms a vector space
under elementwise addition and multiplication by complex scalars.
Proof: Let the original set of ![]() vectors be denoted
vectors be denoted
![]() .
Form
.
Form
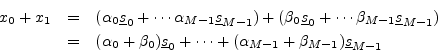
which is yet another linear combination of the original vectors (since
complex numbers are closed under addition). Since we have shown that
scalar multiples and vector sums of linear combinations of the original
![]() vectors from
vectors from ![]() are also linear combinations of those same
original
are also linear combinations of those same
original ![]() vectors from
vectors from ![]() , we have that the defining properties
of a vector space are satisfied.
, we have that the defining properties
of a vector space are satisfied.
![]()
Note that the closure of vector addition and scalar multiplication are ``inherited'' from the closure of complex numbers under addition and multiplication.
Corollary: The set of all linear combinations of ![]() real vectors
real vectors
![]() , using real scalars
, using real scalars
![]() , form a
vector space.
, form a
vector space.
Definition: The set of all linear combinations of a set of ![]() complex vectors from
complex vectors from ![]() , using complex scalars, is called a
complex vector space of dimension
, using complex scalars, is called a
complex vector space of dimension ![]() .
.
Definition: The set of all linear combinations of a set of ![]() real vectors
from
real vectors
from ![]() , using real scalars, is called a real vector
space of dimension
, using real scalars, is called a real vector
space of dimension ![]() .
.
Definition: If a vector space consists of the set of all linear
combinations of a finite set of vectors
![]() , then
those vectors are said to span the space.
, then
those vectors are said to span the space.
Example: The coordinate vectors in ![]() span
span ![]() since every vector
since every vector
![]() can be expressed as a linear combination of the coordinate vectors
as
can be expressed as a linear combination of the coordinate vectors
as

Definition: The vector space spanned by a set of ![]() vectors from
vectors from ![]() is called an
is called an ![]() -dimensional subspace of
-dimensional subspace of ![]() .
.
Definition: A vector
![]() is said to be linearly dependent on
a set of
is said to be linearly dependent on
a set of ![]() vectors
vectors
![]() ,
,
![]() , if
, if
![]() can be expressed as a linear combination of those
can be expressed as a linear combination of those ![]() vectors.
vectors.
Thus,
![]() is linearly dependent on
is linearly dependent on
![]() if there
exist scalars
if there
exist scalars
![]() such that
such that
![]() . Note that the zero vector
is linearly dependent on every collection of vectors.
. Note that the zero vector
is linearly dependent on every collection of vectors.
Theorem: (i) If
![]() span a vector space, and if one of them,
say
span a vector space, and if one of them,
say ![]() , is linearly dependent on the others, then the same vector
space is spanned by the set obtained by omitting
, is linearly dependent on the others, then the same vector
space is spanned by the set obtained by omitting ![]() from the
original set. (ii) If
from the
original set. (ii) If
![]() span a vector space,
we can always select from these a linearly independent set that spans
the same space.
span a vector space,
we can always select from these a linearly independent set that spans
the same space.
Proof: Any ![]() in the space can be represented as a linear combination of the
vectors
in the space can be represented as a linear combination of the
vectors
![]() . By expressing
. By expressing ![]() as a linear
combination of the other vectors in the set, the linear combination
for
as a linear
combination of the other vectors in the set, the linear combination
for ![]() becomes a linear combination of vectors other than
becomes a linear combination of vectors other than ![]() .
Thus,
.
Thus, ![]() can be eliminated from the set, proving (i). To prove
(ii), we can define a procedure for forming the required subset of the
original vectors: First, assign
can be eliminated from the set, proving (i). To prove
(ii), we can define a procedure for forming the required subset of the
original vectors: First, assign ![]() to the set. Next, check to
see if
to the set. Next, check to
see if ![]() and
and ![]() are linearly dependent. If so (i.e.,
are linearly dependent. If so (i.e.,
![]() is a scalar times
is a scalar times ![]() ), then discard
), then discard ![]() ; otherwise
assign it also to the new set. Next, check to see if
; otherwise
assign it also to the new set. Next, check to see if ![]() is
linearly dependent on the vectors in the new set. If it is (i.e.,
is
linearly dependent on the vectors in the new set. If it is (i.e.,
![]() is some linear combination of
is some linear combination of ![]() and
and ![]() ) then
discard it; otherwise assign it also to the new set. When this
procedure terminates after processing
) then
discard it; otherwise assign it also to the new set. When this
procedure terminates after processing ![]() , the new set will
contain only linearly independent vectors which span the original
space.
, the new set will
contain only linearly independent vectors which span the original
space.
Definition: A set of linearly independent vectors which spans a vector space
is called a basis for that vector space.
Definition: The set of coordinate vectors in ![]() is called the natural basis for
is called the natural basis for ![]() , where the
, where the ![]() th basis vector
is
th basis vector
is
![$\displaystyle \underline{e}_n = [\;0\;\;\cdots\;\;0\;\underbrace{1}_{\mbox{$n$th}}\;\;0\;\;\cdots\;\;0].
$](img951.png)
Theorem: The linear combination expressing a vector in terms of basis vectors
for a vector space is unique.
Proof: Suppose a vector
![]() can be expressed in two different ways as
a linear combination of basis vectors
can be expressed in two different ways as
a linear combination of basis vectors
![]() :
:
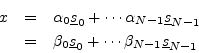
where
![]() for at least one value of
for at least one value of
![]() .
Subtracting the two representations gives
.
Subtracting the two representations gives
Note that while the linear combination relative to a particular basis is
unique, the choice of basis vectors is not. For example, given any basis
set in ![]() , a new basis can be formed by rotating all vectors in
, a new basis can be formed by rotating all vectors in
![]() by the same angle. In this way, an infinite number of basis sets can
be generated.
by the same angle. In this way, an infinite number of basis sets can
be generated.
As we will soon show, the DFT can be viewed as a change of
coordinates from coordinates relative to the natural basis in ![]() ,
,
![]() , to coordinates relative to the sinusoidal
basis for
, to coordinates relative to the sinusoidal
basis for ![]() ,
,
![]() , where
, where
![]() . The sinusoidal basis set for
. The sinusoidal basis set for ![]() consists of length
consists of length
![]() sampled complex sinusoids at frequencies
sampled complex sinusoids at frequencies
![]() . Any scaling of these vectors in
. Any scaling of these vectors in ![]() by complex
scale factors could also be chosen as the sinusoidal basis (i.e., any
nonzero amplitude and any phase will do). However, for simplicity, we will
only use unit-amplitude, zero-phase complex sinusoids as the Fourier
``frequency-domain'' basis set. To summarize this paragraph, the
time-domain samples of a signal are its coordinates relative to the natural
basis for
by complex
scale factors could also be chosen as the sinusoidal basis (i.e., any
nonzero amplitude and any phase will do). However, for simplicity, we will
only use unit-amplitude, zero-phase complex sinusoids as the Fourier
``frequency-domain'' basis set. To summarize this paragraph, the
time-domain samples of a signal are its coordinates relative to the natural
basis for ![]() , while its spectral coefficients are the coordinates of the
signal relative to the sinusoidal basis for
, while its spectral coefficients are the coordinates of the
signal relative to the sinusoidal basis for ![]() .
.
Theorem: Any two bases of a vector space contain the same number of vectors.
Proof: Left as an exercise (or see [46]).
Definition: The number of vectors in a basis for a particular space is called
the dimension of the space. If the dimension is ![]() , the space is
said to be an
, the space is
said to be an ![]() dimensional space, or
dimensional space, or ![]() -space.
-space.
In this book, we will only consider finite-dimensional vector spaces in any detail. However, the discrete-time Fourier transform (DTFT) and Fourier transform (FT) both require infinite-dimensional basis sets, because there is an infinite number of points in both the time and frequency domains. (See Appendix B for details regarding the FT and DTFT.)