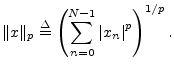Other Lp Norms
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Since our main norm is the square root of a sum of squares,
we are using what is called an 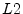 norm and we may write
norm and we may write
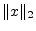 to emphasize this fact.
to emphasize this fact.
We could equally well have chosen a normalized 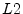 norm:
norm:
which is simply the ``RMS level'' of 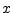 (``Root Mean Square'').
(``Root Mean Square'').
More generally, the (unnormalized) 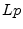 norm of
norm of
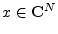 is defined as
is defined as
(The normalized case would include 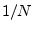 in front of the summation.)
The most interesting
in front of the summation.)
The most interesting 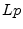 norms are
norms are
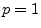 : The
: The 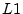 , ``absolute value,'' or ``city block'' norm.
, ``absolute value,'' or ``city block'' norm.
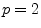 : The
: The 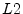 , ``Euclidean,'' ``root energy,'' or ``least squares'' norm.
, ``Euclidean,'' ``root energy,'' or ``least squares'' norm.
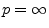 : The
: The
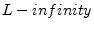 , ``Chebyshev,'' ``supremum,'' ``minimax,''
or ``uniform'' norm.
, ``Chebyshev,'' ``supremum,'' ``minimax,''
or ``uniform'' norm.
Note that the case 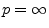 is a limiting case which becomes
is a limiting case which becomes
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy]
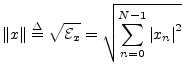
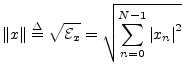
![]() norm:
norm:
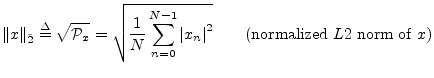
![]() norm of
norm of
![]() is defined as
is defined as