Reconstruction from Samples--The Math

Let $x_d(n) \isdef x(nT)$ denote the $n$th sample of the original sound $x(t)$, where $t$ is time in seconds. Thus, $n$ ranges over the integers, and $T$ is the sampling interval in seconds. The sampling rate in Hertz (Hz) is just the reciprocal of the sampling period, i.e.,

$$f_s\isdef \frac{1}{T}.$$

To avoid losing any information as a result of sampling, we must assume $x(t)$ is bandlimited to less than half the sampling rate. This means there can be no energy in $x(t)$ at frequency $f_s/2$ or above. We will prove this mathematically when we prove the sampling theorem in §D.3 below.

Let $X(\omega)$ denote the Fourier transform of $x(t)$, i.e.,

$$X(\omega)\isdef \int_{-\infty}^\infty x(t) e^{-j\omega t} dt .$$

Then we can say $x$ is bandlimited to less than half the sampling rate if and only if $X(\omega)=0$ for all $\vert\omega\vert\geq\pi f_s$. In this case, the sampling theorem gives us that $x(t)$ can be uniquely reconstructed from the samples $x(nT)$ by summing up shifted, scaled, sinc functions:

$${\hat x}(t) \isdef \sum_{n=-\infty}^\infty x(nT) h_s(t-nT) \equiv x(t)$$

where

$$h_s(t) \isdef$$   sinc$$(f_st) \isdef \frac{\sin(\pi f_st)}{\pi f_st}.$$

The sinc function is the impulse response of the ideal lowpass filter. This means its Fourier transform is a rectangular window in the frequency domain. The particular sinc function used here corresponds to the ideal lowpass filter which cuts off at half the sampling rate. In other words, it has a gain of 1 between frequencies 0 and $f_s/2$, and a gain of zero at all higher frequencies.

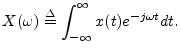
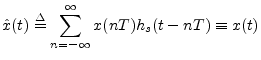
The reconstruction of a sound from its samples can thus be interpreted as follows: convert the sample stream into a weighted impulse train, and pass that signal through an ideal lowpass filter which cuts off at half the sampling rate. These are the fundamental steps of digital to analog conversion (DAC). In practice, neither the impulses nor the lowpass filter are ideal, but they are usually close enough to ideal that one cannot hear any difference. Practical lowpass-filter design is discussed in the context of bandlimited interpolation [70].