19．纽科姆悖论

	M：一天，一个由外层空间来的超级生物欧米加在地球着陆。
	M：欧米加搞出一个设备来研究人的大脑。他可以十分准确地预言每一个人在二者择一时会选择哪一个。
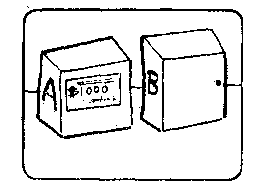
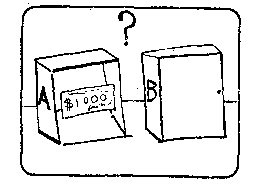
	M：欧米加用两个大箱子检验了很多人。箱子A是透明的，总是装着1千美元。箱子B不透明，它要么装着1百万美元，要么空着。
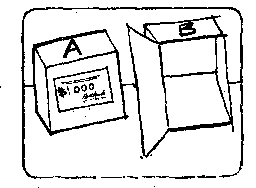
	M：欧米加告诉每一个受试者。 欧米加：你有两种选择，一种是你拿走两个箱子，可以获得其中的东西。可是，当我预计你这样做时，我就让箱子B空着。你就只能得到1千美元。
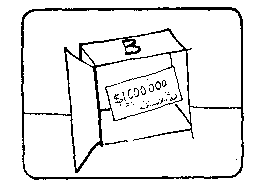
	欧米加：另一种选择是只拿一个箱子B。如果我预计你这样做时，我就放进箱子B中1百万美元。你能得到全部款子。
	M：这个男人决定只拿箱子B。他的理由是—— 男：我已看见欧米加尝试了几百次，每次他都预计对了。凡是拿两个箱子的人，只能得到l千美元。所以我只拿箱子B，就可变成一个百万富翁。
	M：这个女孩决定要拿两个箱子，她的理由是—— 女：欧米加已经做完了他的预言，并已离开。箱子不会再变了。如果是空的，它还是空的。如果它是有钱的，它还是有钱。所以我要拿两个箱子，就可以得到里面所有的钱。
	M：你认为谁的决定最好？两种看法不可能都对。哪一种错了？它为何错了？这是一个新的悖论，而专家们还不知道如何解决它。

这个悖论是哲学家经常争论的很多预言悖论中最新的，也是最棘手的。它是物理学家威廉·纽科姆发明的，称为纽科姆悖论。哈佛大学的哲学家罗伯特·诺吉克首先发表并分析了这个悖论。他分析的依据主要是数学家称之为“博弈论”或“对策论”的法则。

男孩决定只拿B箱是很容易理解的。为了使女孩的论据明显起来，要记住欧米加已经走了。箱子里也许有钱，也许空着，这是不会再改变的。如果有钱，它仍然有钱；如果空着，它仍然空着。让我们思考一下这两种情况。

如果B中有钱，女孩只拿箱子B，她得到1百万美元。如果她两个箱子都要，就会得到1百万加1千元。

如果B箱空着，她只拿B箱，就什么也得不到。但如果她拿两个箱子，她就至少得到1千美元。

因此，每一种情况下，女孩拿两个箱子都多得1千元。

这条悖论，是试验一个人是否相信自由意志论的“石蕊试纸”类型的悖论。对这个悖论的反应公平地区分出，愿意拿两个箱子的是自由意志论信徒，愿意拿B箱者是决定论（宿命论）信徒。而另一些人则争辩道：不管未来是完全决定的，还是不是完全决定的，这个悖论所要求的条件却是矛盾的。

对这些争论观点的讨论可参见马丁·加德勒在1973年《科学美国人》7月号的数学游戏专栏，以及诺吉克教授发表在同一刊物1974年3月号同一专栏的文章。由于这一悖论还未解决，故它是学生讨论的极好课题。你将发现课堂里对这个悖论的反应是活跃的，十分有益的。