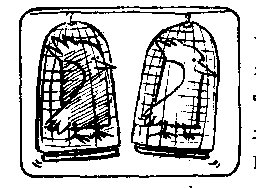
8．鹦鹉之谜

	M：一位夫人有两只鹦鹉。一天一个来访者问她。 来访者：“有一只鹦鹉是雄的吗？” 夫人：“对，有一只是雄的”。 M：两只鹦鹉都是雄的概率是几呢？
	M：假定那个人问另一个问题： 来访者：绿鹦鹉是雄的吗？ 夫人：是。 M：现在，两只鸟都是雄的，概率提高到1/2。为什么一问到绿鹦鹉是不是雄的就改变了概率？
	M：这条悖论在把一切同等可能情况都列出之后，就很容易解释了。当这个人问是否有一只鹦鹉是雄的时，有三种可能的情况要考虑到。其中只有一种是两只都是雄的，所以这种情况的概率是1/3。
	M：可是，在这个人问绿鹦鹉是否雄的时，就只有两种情况要考虑。其中一种是两只都是雄的，所以这种情况的概率是1/2。

现在可用两个硬币来模拟鹦鹉问题，一个用2分的硬币，一个用一分的硬币，让一个学生抛掷，然后就其结果作出某些论断。该学生可以采取几种做法：

1．如果两枚硬币都是国徽，他说：“至少有一枚硬币是国徽。”如果两枚硬币都是字，他说：“至少有一枚硬币是字。”如果两枚硬币不相同，他说：“至少有一枚是……。”（国徽和字由他随便说一个）。无论他说的是什么，两个硬币都是一样的概率是什么？是1/2。

2．这个学生进而又同意只是在出现国徽时才叫：“至少有一枚硬币是国徽。”如果没有一枚硬币是国徽，他就什么也不说，重来一次。这时，两枚硬币那是国徽的概率是多少？1/3（因为现在两枚都是字的情况已排除在外了）。

3．学生进而又同意按一分硬币落下的情况较，即按一分硬币的国徽朝上或字朝上叫。这时，两个硬币一样的概率是多少？回答1/2。

4．学生又同意这样叫：只当一分的硬币是国徽时才叫：“至少有一枚是国徽。”这时两枚硬币都是国徽的概率是多少？回答：1/2。

好一点的学生不用试验就可作出正确回答。你的班级一定高兴做几次实际试验来验证这些答案。

鹦鹉悖论有时在教科书中以一种含糊的方式给出，结果不可能有正确回答。例如，你假定碰到一个陌生人，他说：“我有两个孩子，至少有一个是男孩。”那么两个孩子都是男孩的概率是几？

这是一个定义得不准确的问题，因为你对使这个人说出上面那些话的环境一无所知，很可能是这样：如果他两个孩子性别不同，他就随便挑一个说，或许他说过“至少有一个是女孩。”也可能两个孩子都一样，则他就如上面那样说出他们的性别来。如果他是这样的过程，则二者一样的概率就是1/2。情况同上面的第一种。

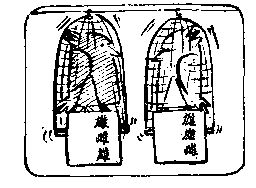
画中顾客用提问方法消除了模糊：顾客第一次问道“至少一只鸟是雄的吗？”相应于上述第二种情况。他第二次又问：“绿鸟是雄的吗?”对应了第四种情况。

还有一个使人惊愕的悖论，与鹦鹉悖论很有关系，叫做第二张A的悖论。假定你正在玩桥牌。在发完牌时，你扫视一下手中的牌，宣布：“我有一张A。”那么你还有一张A的概率是多少？它是严格的，小于1/2。

现在假定，大家一致同意专指一张A，比如果桃A，桥牌一直打到你可以叫：“我有一张黑桃A”时，你还有一张A的概率是几？这，稍高于1/2！为什么指定了A的花色就改变了概率？

对一手牌的全部可能作出计算是冗长乏味的，不过若把一手牌减为四张，就可以理解这条悖论的奥妙了。比如说这四张牌是黑桃A，红心A，梅花2和方块J（通过减少其元素个数来简化问题往往是了解其结构的绝妙方法）。洗一洗这四张牌，把它发给两个人，两张牌一手有六种同等可能的情况。

♠A ♥A

♠A ♦J

♠A ♣2

♥A ♦J

♥A ♣2

♦J ♣2

六手牌中有五手（即前五手牌）都使玩牌者可以说“我有一张A”。但五手牌中只有一手是还有一张A的，结果有第二张A的概率是1/5。

上面有三手牌（即前三手牌）使玩牌人可以宣布：“我有一张黑桃A”。这三手中只有一手是有另一张A的，两张A的概率是1/3。

这样变一下就很简单了，课堂上可以验证一下，比如说，将这四张牌洗、发五十次，全部记录下来。如果一个学生知道了它的公式，又有小计算器，他也许高兴对整副牌来试解上面的问题。

注意，要叫的A和叫牌的人都必须预先定好，如果这些假定未事先定好，问题就不明确确定。