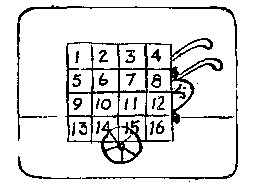7．奇妙的方阵

	M：把这个4行4列的方阵画在一张纸上，将1到16等数字填入格中。我现在举一个著名例子，证明人的精神的威力，这定会使你吃惊！我能够把握你在这个方阵中选择的4个数。
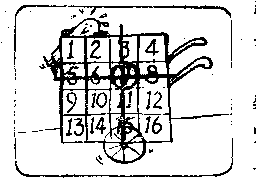
	M：在这个方阵中任意选一个数并画上圈。这个画片中圈的是7，可是你可以圈你自己选出的数。现在将圈出的数所在的那—竖行（称为列）划一条竖直线，再将这个数所在的横行（称为行）划一横线。
	M：在没有划线的数中，选一个数并画上圈。又按上面的方法将这个数所在的行和列划线。再选第三个没有划线的数，将这个数所在行和列划线。最后把仅余下来的一个数画圈。
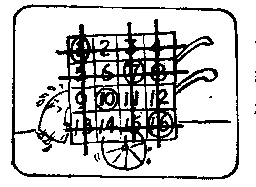
	M：如果你按上法进行，则你的方阵就有点像这张画中的样子。现在，把你选出的画圈的4个数加起来。
	M：你做完了吗？我现在告诉你们每个人你们加得的总数。它…是…34！对不对？我怎么知道的？我真的能左右你的选择吗？

为什么这个方阵会使得我们选出的四个数加起来总是得34？秘诀巧妙而简单。在4*4的方阵的第一行的上面顺次写4个数1、2、3、4。在第一列的左边写4个数0、4、8、12。

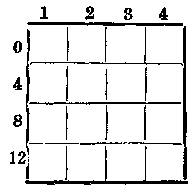
这8个数称为魔法方阵的“生成元”。方阵中每一格可以填上由这一格所在列上方的生成元与所在行左边的生成元相加得到的数。按这个方法将方阵中所有格子填满之后，我们的方阵就按从1到16的顺序填满了。

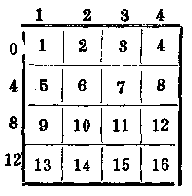
现在我们就可以看一看按前面讲的步骤圈出4个数时有什么特点。显然，上面步骤保证圈出的4个数不会在同一行或同一列。每一个圈出的数都是两个生成元的和，由于它们各在不同的行和列，故4个数的生成元各不相同，因此这4个数的和就等于全部8个生成元的和。这8个生成元相加等于34，所以圈出的4个数的和总是34。

当学生们明白了方阵的窍门后，他们就能编出各种不同大小的方阵来了。比如，我们考虑一个6阶的方阵，它有12个生成元。注意，在这个例子中，选取的生成元使得方阵内数字看起来好像是完全随意的。这里面暗含看这个方阵数字的结构基础，从而使之更富神秘色彩。

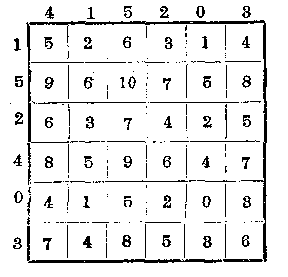
所有生成元的和是30。如果照前面画片中说明的步骤来选择数字的话，最后选出的所有数之和应为30。自然，那个有肯定结果的数字（或和数）的大小可以由我们任意挑。

如果构成一个10行10列的方阵，使选出的和为100，或任何其他有趣的数，例如当年的年份或某人的出生年分等，这会激发起热烈的气氛。

魔法方阵可否在格中填负数？当然可以！事实上，生成元可以是任意实数：正数或负数、有理数或无理数。

魔法矩阵可否采用乘法，就是选出的数彼此相乘得一定数？可以。这可以引起学生们探讨另一条途径。基本结构完全相同。这时方阵格中的数是一组生成元的乘积。我们也许还希望看看，如果格中填入了一组复杂的数，会产生什么结果。关于魔法方阵的更多的内容可以在《科学美国人》杂志出的《数学之谜和数学游戏》一书第二章中找到。