8．使人为难的编织问题

	M：文迪女士要买一个皮手镯。
	M：在卢克的商店里她看到两个手镯，每个都由三条带构成，其中一个已经编好了，另一个还没有编。
	文迪：编好的那个手镯要多少钱？ 卢克：五美元，太大。但您来晚了，它已经卖出了。
	文迪：唷！还有手镯可买吗？ 卢克：还有这个。 文迪；可是它还没有编呢？ 户克：我很乐意为您把它编好，太太。
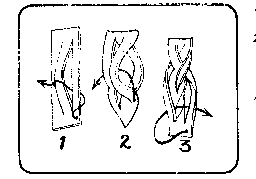
	M：这看来好象是不可能的，但是卢克仅用30秒钟就把它编好了，并且没有切断一条带。你看，他是这样开始编的。

大多数学生仅仅把这手镯当成拓扑学的又一奇观，但还不止于此。著名的德国数学家艾米尔·阿尔丁创立了一套有关“编织”的理论，其中用到了群论。在这个群里，“元素”是指“编织式样”，而“运算”是指让一个式样紧随另一式样因而产生一个新式样的过程。而“逆元素”则是指式样的镜象。编织问题为群论和变换理论提供了一个极好的起点。载于《数学教师》杂志1959年5月号上阿尔丁的文章“编织理论”是一个很好的入门教材。

令人惊异的是，在这个有六处交叉的手镯编织过程中，三条带子的端部始终是连结在一起的。这就意味著，编好的手镯与没编的手镯是拓扑等价的。下图表示的是编手镯的步骤。

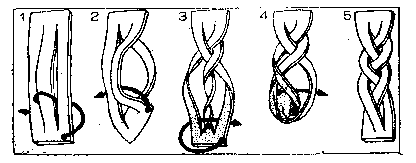
如果带子再长一些，我们就可以重复使用这个步骤，只要带子足够长，编成的手镯的交叉数可以是6的任意倍数。如果学生们想用这种方法把硬皮革做成一个实用的手镯或编带，则需把皮革浸在热水里使之变得柔软以后再进行编织。

对多于三条带子组成的手镯也可以用这种方法编织。要想进一步了解这方面的知识请读J.A.H. 谢泼德的文章“对两端分别连在一起的若干条带子进行编织”，载于《皇家学会会报，A》第265卷（19623年），229——244页。