Arithmetic and Variables

3.1 Integer Arithmetic

How do you calculate the value of your spare change? No doubt, you separate into groups your quarter coins (25-cent pieces), dimes (10-cent pieces), nickels (5-cent pieces), and pennies (1-cent pieces). Once you count the quantity of each, you multiple each quantity by the value of the coin and total the amounts.

For example, if you have 9 quarters, 2 dimes, no nickels, and 6 pennies, you would calculate this total:

(9 times 25) plus (2 times 10) plus (0 times 5) plus (6 times 1) 

If your arithmetic skills are weak, you can embed the above computation into a simple Java program and have the computer do it for you, because the Java language lets you write arithmetic expressions like 9 * 25 (the * means multiplication) and (9 * 25) + (2 * 10) (the + means addition), and so on---symbols like * and + are called operators, and the operators' arguments (e.g., 9 and 25 in 9 * 25) are their operands.

Here is the program that does the calculation:

/** Total computes the amount of change I have, based on
  * 9 quarters, 2 dimes, no nickels, and 6 pennies */
public class Total
{ public static void main(String[] args)
  { System.out.println("For 9 quarters, 2 dimes, no nickels, and 6 pennies,");
    System.out.print("the total is ");
    System.out.println( (9 * 25) + (2 * 10) + (0 * 5) + (6 * 1) );
  }
}

For 9 quarters, 2 dimes, no nickels, and 6 pennies,
the total is 251

System.out.println( (9 * 25) + (2 * 10) + (0 * 5) + (6 * 1) );

If a comment, like the one in the above example, extends across multiple lines, we begin each new line with an asterisk; the reason is explained in Chapter 5.

In the Java language, whole numbers, like 6, 0, 251, and -3, are called integers. We see momentarily that the Java language uses the keyword, int, to designate the collection of integers.

Begin Footnote: More precisely, int is Java's name for those integers that can be binary coded within one computer word, that is, the integers in the range of -2 billion to 2 billion. End Footnote.

Of course, you can write Java programs to do other numerical calculations. For the moment, consider addition (+), subtraction (-), and multiplication (*); you can use these in a Java program the same way you write them on paper, e.g.,

1 + ((2 - 4) * 3) + 5

public class Test
{ public static void main(String[] args)
  { System.out.println(1 + ((2 - 4) * 3) + 5); }
}

    1 + ((2 - 4) * 3) + 5 
=>  1 + ((-2) * 3) + 5 
=>  1 + (-6) + 5 
=>  -5 + 5  =>  0

Exercises

1. 6 * ((-2 + 3) * (2 - 1))
2. 6 * (-2 + 3) * (2 - 1)
3. 6 * -2 + 3 * (2 - 1)
4. 6 * -2 + 3 * 2 - 1

3.2 Named Quantities: Variables

Used in the simplest way, a variable is a just a name for an integer, just like ``Lassie'' is just a name for your pet dog.

Begin Footnote: But as already noted in Chapter 2, a variable name is in reality a storage cell that holds the named integer. For the moment, don't worry about the storage cell; this detail is revealed only when necessary in a later section. End Footnote

To give the name, quarters, to the integer, 9, we write this Java statement:

int quarters = 9;

This form of statement is called a variable declaration; more precisely, it is a variable initialization, because it creates a new variable and initializes it with a numerical value. The keyword, int, is a data type---it names a ``type'' or ``species'' of data value, namely the integers. The keyword, int, tells the Java compiler that the value of quarters, whatever it might be, must be from the data type int.

Since the variable, quarters, names an integer, we use it just like an integer, e.g.,

System.out.println(quarters * 25);

Indeed, when the Java compiler examines a reference to a variable, like the one in the previous statement, it verifies that the variable's data type (here, int) is acceptable to the context where the variable is referenced (here, the variable is multiplied by 25---this is an acceptable context for referencing variable quarters). This examination by the Java compiler, called data-type checking---prevents problems which might arise, say, if an int-typed variable was referenced in a context where a string was expected.

When we need to distinguish between variables, like quarters, that denote integers, and actual integers like 6 and 225, we call the latter literals.

The name you choose for a variable is called an identifier; it can be any sequence of letters, numerals, or the underscore, _, or even a dollar sign, $ (not recommended!), as long the name does not begin with a numeral, e.g., quarters or QUArTers or my_4_quarters. But Java keywords, like public and class, cannot be used as variable names.

Here is an improved version of the change-counting example in the previous section; it names each of the four quantities and prints a detailed description of the quantities and their total. Here is what the program prints:

For these quantities of coins:
Quarters = 9
Dimes = 2
Nickels = 0
Pennies = 6
The total is 251

FIGURE 1: change computing program=======================================

/** TotalVariables  computes the amount of change I have, based on the values
  * named by the four variables,  quarters, dimes, nickels, and  pennies. */
public class TotalVariables
{ public static void main(String[] args)
  { int quarters = 9;
    int dimes = 2;
    int nickels = 0;
    int pennies = 6;

    System.out.println("For these quantities of coins:");
    System.out.print("Quarters = ");
    System.out.println(quarters);
    System.out.print("Dimes = ");
    System.out.println(dimes);
    System.out.print("Nickels = ");
    System.out.println(nickels);
    System.out.print("Pennies = ");
    System.out.println(pennies);
    System.out.print("The total is ");
    System.out.println( (quarters * 25) + (dimes * 10)
                           + (nickels * 5) + (pennies * 1) );
  }
}

ENDFIGURE================================================================

It is easy to see the four variables and understand how they are referenced for change calculation. Now, if you wish to modify the program and calculate a total for different quantities of coins, all you must do is change the appropriate variable initializations, and the remainder of the program works correctly.

We finish the change calculation example with this last improvement: We make the total print as dollars and cents, like so:

For these quantities of coins:
Quarters = 9
Dimes = 2
Nickels = 0
Pennies = 6
The total is 2 dollars and 51 cents

251 / 100 computes to 2,

The remainder part of an integer divison is calculated by the remainder (``modulo'') operator, %:

251 % 100 computes to 51,

To use this technique, we write these statements:

int total = (quarters * 25) + (dimes * 10) + (nickels * 5) + (pennies * 1);
System.out.print("The total is ");
System.out.print(total / 100);
System.out.print(" dollars and ");
System.out.print(total % 100);
System.out.println(" cents");

The total is 2 dollars and 51 cents

The long sequence of print statements just seen can be compressed into just one with this Java ``trick'': When a textual string is ``added'' to another string or an integer, a longer string is formed. For example

System.out.println("Hello" + "!");
System.out.println("Hello" + (48 + 1));

Hello!
Hello49

System.out.println("The total is " + (total / 100) + " dollars and "
   + (total % 100) + " cents");

Figure 2 exploits everything we have learned in the final version of the change-calculation program.

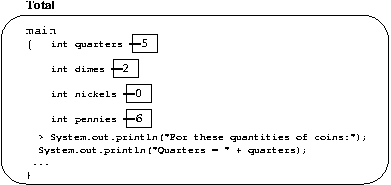
FIGURE 2: Calculating the value of change================================

/** Total computes the amount of change I have, based on
    the values named by the variables,
    quarters, dimes,  nickels,  and   pennies */
public class Total
{ public static void main(String[] args)
  { int quarters = 5;
    int dimes = 2;
    int nickels = 0;
    int pennies = 6;

    System.out.println("For these quantities of coins:");
    System.out.println("Quarters = " + quarters);
    System.out.println("Dimes = " + dimes);
    System.out.println("Nickels = " + nickels);
    System.out.println("Pennies = " + pennies);
    int total = (quarters * 25) + (dimes * 10) + (nickels * 5) + (pennies * 1);
    System.out.println("The total is " + (total / 100) + " dollars and "
       + (total % 100) + " cents");
  }
}

ENDFIGURE===============================================================

Exercises

1. Modify the application in Figure 1 so that it calculates the value of 3 quarters and 12 nickels; compile it and execute it.
2. Modify the application in Figure 1 so that it displays the value of each group of coins and then the value of all the coins. Try the application for 4 quarters, 1 nickel, and 1 penny. The application should reply:

   For these quantities of coins:
   Quarters = 4, worth 100 cents
   Dimes = 0, worth 0 cents
   Nickels = 1, worth 5 cents
   Pennies = 1, worth 1 cents
   The total is 106 cents
   

3. Modify Figure 2 so that it displays its output in decimal format, e.g.,

   The total is $2.51
   

   Explain what happens when the modified application is used with the quantities of coins listed in the previous Exercise. (We will repair the difficulty in the section, ``Converting between Strings and Numbers and Formatting.'')
4. For practice, write an application in Java that prints a multiplication table of all pairs of numbers between 1 and 3, that is, 1*1, 1*2, and so on, up to 3*3.

3.2.1 Variables Can Vary: Assignments

As the examples in the previous section showed, variables name numerical quantities. But they can do more than that---the value that a variable names can change as a computation proceeds. Unlike the variables in algebra, computer variables can truly vary.

Here's why: When a variable is initialized, a storage cell in primary storage is created, and the number named by the variable is placed into the cell. Here is a picture of the object created in primary storage by class Total in Figure 2 just after the four variables are initialized:

The above picture is important, because the Java language allows you to change the value held in a variable's cell; you use a statement called an assignment. Here is a small example, where a variable, money, is initialized to 100, and then the money is completely withdrawn:

int money = 100;
System.out.println(money);
money = 0;
System.out.println(money);

100
0

A more interesting example creates a variable to hold money and then deposits 50 more into it:

int money = 100;
System.out.println(money);
money = money + 50;
System.out.println(money);

We use the power of assignments to write another classic program with change: Say that we desire a program that prints the coins one needs to convert a dollars-and-cents amount into coins. For example, if we have 3 dollars and 46 cents, the program reports that we receive this change:

quarters = 13
dimes = 2
nickels = 0
pennies = 1

If you solved this problem on a street corner, you would first count the number of quarter-dollar coins that are needed and subtract the amount of quarters from the starting money (e.g., 3.46 - (13*0.25) = 0.21). Then, you would repeat the process for dimes (0.21 - (2*0.10) = 0.01), nickels (0.01 - (0*0.5) = 0.01) and pennies. The value of the remaining money decreases from 3.46 to 0.21 to 0.01 to 0.

Here is the algorithm for the change-making method:

1. Set the starting value of money.
2. Subtract the maximum number of quarters from money, and print the quantity of quarters extracted.
3. Subtract the maximum number of dimes from money, and print the quantity of dimes extracted.
4. Subtract the maximum number of nickels from money, and print the quantity of nickels extracted.
5. The remainder of money is printed as pennies.

int dollars = 3;
int cents = 46;
int money = (dollars * 100) + cents;

System.out.println("quarters = " + (money / 25));
money = money % 25;

In the first statement, money / 25 calculates the maximum number of quarters to extract from money. There are two important points:

1. The integer division operator, /, calculates integer quotient---the number of times 25 can be subtracted from money without leaving a negative remainder. In the example, since money's cell holds 346, the quotient is 13, because a maximum of 13 quarters (13*25 = 325) can be wholly subtracted from 346 without leaving a negative remainder. Here are additional examples for intuition:
   • 14 / 3 computes to 4 (and the remainder, 2, is forgotten)
   • 6 / 3 computes to 2 (and there is no remainder)
   • 4 / 5 computes to 0, because 5 cannot be wholly subtracted from 4
2. The calculation of the division, money / 25, does not alter the value in money's cell, which remains 346---only an assignment statement can change the value in money's cell.

The second statement, money = money % 25, deals with the second point just mentioned: Since we have calculated and printed that 13 whole quarters can be extracted from the amount of money, we must reset the value in money's cell to the remainder. This can be done either of two ways:

1. By the statement,

   money = money - ((money / 25) * 25);
   

   which calculates the monetary value of the extracted quarters and subtracts this from money.
2. By the more elegant statement,

   money = money % 25;
   

   whose modulo operator, %, calculates the integer remainder of dividing money by 25 and assigns it to money. In this example, the remainder from performing 346/25 is of course 21. Here are additional examples of computing remainders:
   • 14 % 3 computes to 2
   • 6 % 3 computes to 0
   • 4 % 5 computes to 4

The combination of the integer quotient and remainder operations calculates the correct quantity of quarters. We apply this same technique for computing dimes and nickels and see the resulting program in Figure 3.

FIGURE 3: change-making program=========================================

/**  MakeChange calculates the change for the amounts in variables
  *   dollars  and  cents.  */
public class MakeChange
{ public static void main(String[] args)
  { int dollars = 3;
    int cents = 46;
    int money = (dollars * 100) + cents;
    System.out.println("quarters = " + (money / 25));
    money = money % 25;
    System.out.println("dimes = " + (money / 10));
    money = money % 10;
    System.out.println("nickels = " + (money / 5));
    money = money % 5;
    System.out.println("pennies = " + money); }
}

ENDFIGURE===============================================================

When the application starts, the main method executes, and the three variable initializations create three cells:

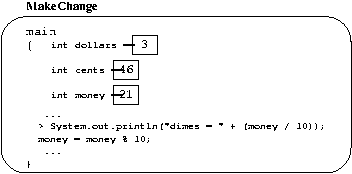
The circular-appearing assignments in the example, like money = money % 25, might distress you a bit, because they look like algebraic equations, but they are not. The semantics of the previous assignment statement proceeds in these three steps:

1. The variable cell named by money is located
2. The expression, money % 25, is computed to an answer, referencing the value that currently resides in money's cell.
3. The answer from the previous step is placed into money's cell, destroying whatever value formerly resided there.

Finally, because of the existence of the assignment statement, it is possible to declare a valueless variable in one statement and assign to it in another:

int dollars;  // this is a declaration of  dollars;  it creates a cell
dollars = 3;  // this assigns 3 to the cell

Exercises

1. Revise the program, in Figure 3 so that it makes change in terms of five-dollar bills, one-dollar bills, quarters, dimes, nickels, and pennies.
2. What are the results of these expressions? 6/4; 6%4; 7/4; 7%4; 8/4; 8%4; 6/-4; -6%4; 6%-4.
3. Use algebra to explain why the assignment, money = money % 25, in the MakeChange program correctly deducts the number of a quarters from the starting amount of money.
4. Write this sequence of statements in Java:
   • A variable, my_money, is initialized to 12.
   • my_money is reduced by 5.
   • my_money is doubled.
   • my_money is reset to 1.
   • The value of my_money is sent in a println message to System.out.
5. Write an execution trace of this application:

   public class Exercise3
   { public static void main(String[] args)
     { int x = 12;
       int y = x + 1;
       x = x + y;
       y = x;
       System.out.println(x + " equals " + y);
     }
   }
   

3.3 Arithmetic with Fractions: Doubles

f = (9.0/5.0)*c + 32

Double literals are conveniently written as decimal fractions, e.g., 9.0 and -3.14159, or as mantissa-exponent pairs, e.g., 0.0314159E+2, which denotes 3.14159 (that is, 0.0314159 times 10²) and 3E-6, which denotes .000003 (that is, 3 times 1/10⁶).

Java allows the classic arithmetic operations on doubles: addition (whose operator is +), subtraction (-), multiplication (*), and division (/). Given fractional (double) operands, the operations calculate doubles as results. For example, we can write (1.2 + (-2.1 / 8.4)) * 0.33, and the computer calculates

    (1.2 + (-2.1 / 8.4)) * 0.33
=>  (1.2 + (-0.25)) * 0.33
=>  (0.95) * 0.33  =>  0.3135

Returning to the temperature conversion formula, we write it as a Java application. The key statements are these two:

int c = 22;
double f = ((9.0/5.0) * c) + 32;

It is acceptable to mix integers, like c, with doubles in an expression---the result will be a double, here, 71.6. (This is the case even when the fraction part of the result is zero: 2.5 * 4 computes to 10.0.)

The preceding examples present an important point about the basic arithmetic operations, +, -, *, and /:

• When an arithmetic operation, like +, is applied to two arguments of data type int, e.g., 3 + 2, then the result of the operation is guaranteed to be an integer---have data type int---as well.
• When an arithmetic operation is applied to two numerical arguments, and at least one of the arguments has type double, e.g., 3 + 2.5, then the result is guaranteed to have type double.

The completed temperature program is simple; see Figure 4.

FIGURE 4: temperature conversion========================================

/**  CelsiusToFahrenheit converts a Celsius value to Fahrenheit.  */
public class CelsiusToFahrenheit
{ public static void main(String[] args)
  { int c = 22;   // the degrees Celsisus
    double f = ((9.0/5.0) * c) + 32;
    System.out.println("For Celsius degrees " + c + ",");
    System.out.println("Degrees Fahrenheit = " + f);
  }
}

ENDFIGURE===============================================================

For Celsius degrees 22,
Degrees Fahrenheit = 71.6

In addition to fractional representation, the Java language lets you write doubles in exponential notation, where very large and very small doubles are written in terms of a mantissa and an exponent. For example, 0.0314159E+2 is the exponential-notation representation of 3.14159. (You see this by multiplying the mantissa, 0.0314159, by 10², which is 10 raised to the power of the exponent, 2.) Another example is 3e-6, which denotes .000003 (that is, 3 times 1/10⁶)---it doesn't matter whether the E is upper or lower case.

Mathematicians and engineers who work with doubles often require operations such as exponentiation, square root, sine, cosine, and so on. The Java designers have assembled a class, named Math, that contains these methods and many more. For example, to compute the square root of a double, D, you need only say, Math.sqrt(D):

double num = 2.2;
System.out.println("The square root of " + num + " is " + Math.sqrt(num));

Although doubles and integers coexist reasonably well, complications arise when numbers of inappropriate data types are assigned to variables. First, consider this example:

int i = 1;
double d = i;

In contrast, the Java compiler refuses to allow this sequence,

double d = 1.5;
int i = d + 2;

If the programmer truly wants to lose the fractional part of 3.5, she can use a cast expression to indicate this:

double d = 1.5;
int i = (int)(d + 2);

Exercises

1. Rewrite the program, CelsiusToFahrenheit, into a program, FahrenheitToCelsius, that converts a double value of Fahrenheit degrees into double value of Celsius degrees and prints both values.
2. Recall that one kilometer is 0.62137 of a mile. Rewrite the program, CelsiusToFahrenheit, into a program, KilometersToMiles, that takes as input an integer value of kilometers and prints as output a double value of the corresponding miles.
3. Calculate the answers to these expressions; be careful about the conversions (casts) of integer values to doubles during the calculations:
   1. (5.3 + 7) / 2.0
   2. (5.3 + 7) / 2
   3. 5.3 + (7 / 2)
   4. (1.0 + 2) + ((3%4)/5.0)

3.4 Booleans

System.out.println( 6 > (4.5 + 1) );

The Java data type, boolean, consists of just the two values, true and false.

Booleans are used as answers to questions; here is an example: We employ the temperature conversion formula to determine whether a given Celsius temperature is warmer than a given Fahrenheit temperature. The algorithm is

1. Set the given Celsius and Fahrenheit temperatures.
2. Convert the Celsius amount into Fahrenheit.
3. Compare the converted temperature to the other Fahrenheit temperature.

double C = 22.0;
double F = 77.0;
double C_converted = ((9.0/5.0) * C) + 32;
System.out.print(C + " Celsius warmer than " + F + " Fahrenheit?  ");
System.out.println(C_converted > F);

22.0 Celsius warmer than 77.0 Fahrenheit?  false

Here are the standard comparison operations on numbers. All these operations use operands that are integers or doubles and all compute boolean results:

Operation	Operator symbol	Example
greater-than	>	6 > (3 + 1) calculates to true
less-than	<	6.1 < 3 calculates to false
less-than-or-equals	<=	(3.14 * -1) <= 0 calculates to true
greater-than-or-equals	>=	1 >= 2 calculates to false
equality	==	(1 + 2) == (2 + 1) calculates to true
inequality	!=	0.1 != 2.1 calculates to true

It is perfectly acceptable to save a boolean answer in a variable:

boolean b = (3 < 2);

boolean b = false;

b = ((3 * 2) == (5 + 1));

b = (3 * 2 == 5 + 1);

b =  3 * 2 == 5 + 1;

Finally, the usual numerical operations (+, -, *, / , %) cannot be used with boolean arguments, because it makes no sense to ``add'' or ``subtract'' logical truths. (E.g., what would true - false mean?) The Java compiler will report an error message if you attempt such actions.

Exercises

1. Build a complete Java application that uses the technique in this section to determine whether a given celsius temperature is warmer than a given fahrenheit temperature. Test the application with 40 Celsisus and 40 Fahrenheit.
2. Build a Java application that is told a quantity of dimes and a quantity of nickels and prints whether the quantity of dimes is worth less than the quantity of nickels. Test the application with 4 dimes and 6 nickels.
3. Calculate the results of these expressions:
   1. (3 * 2) >= (-9 - 1)
   2. 3 * 2 != 5.5 + 0.4 + 0.1

3.5 Operator Precedences

When the Java interpreter calculates an arithmetic expression, it proceeds from left to right: Given an expression of the form, EXPRESSION1 operator EXPRESSION2, the interpreter evaluates EXPRESSION1 to its result before it evaluates EXPRESSION2 and then applies the operator to the two resulting values.

Parentheses within an expression are highly recommended to make clear which expressions belong as operands to which operators. Consider 1 * 2 + 3--what is the * operator's second operand? Is it 2? Or 2 + 3? If the expression was properly parenthesized, as either 1 * (2 + 3) or (1 * 2) + 3, this confusion would not arise.

If parentheses are omitted from an expression that contains multiple operators, the Java compiler will apply its own rules to direct the computation of the Java interpreter. These rules, called operator precedences, are listed shortly.

One simple and ``safe'' example where parentheses can be omitted is a sequence of additions or multiplications, e.g., 1 + 2 + 3 or 1 * 2 * 3. There is no confusion here, because both addition and multiplication are associative---the order that the additions (multiplications) are performed does not affect the result.

When multiplications and divisions are mixed with additions and subtractions in an expression without parentheses, the interpreter still works left to right, but when there is a choice, the interpreter does multiplications and divisions before additions and subtractions. We say that the precedences of multiplication and division are higher than those of addition and subtraction. For example, 1 + 2.0 * 3 results in 7.0, because there is a choice between computing 1 + 2.0 first or 2.0 * 3 first, and the Java interpreter chooses the latter, that is, the multiplication is performed just as if the expression was bracketed as 1 + (2.0 * 3).

Here is the ordering of the precedences of the arithmetic operations, in the order from highest precedence (executed first, whenever possible) to lowest (executed last):

unary negation, e.g., -3

multiplication, *, division/quotient, /, and modulo %

addition/string concatenation, +, and subtraction, -

comparison operations, <, <=, >, >=

comparisons of equality, ==, and inequality, !=

Although it is not recommended to write expressions like the following one, the precedence rules let us untangle the expression and compute its answer:

    3 + -4 * 5 != 6 - 7 - 8
=>  3 + -20 != 6 - 7 - 8
=>  -17 != 6 - 7 - 8
=>  -17 != -1 - 8
=>  -17 != -9
=>  true

Exercises

1. Calculate the answers for each of these expressions:
   1. 6 * -2 + 3 / 2 - 1
   2. 5.3 + 7 / 2 + 0.1
   3. 3*2%4/5.0*2*3
2. Another way of understanding operator precedences is that the precedences are rules for inserting parentheses into expressions. For example, the precedences tell us that the expression 1 + 2.0 * 3 should be bracketed as 1 + (2.0 * 3). Similarly, 5 - 3 / 2 * 4 + 6 * -2 / -3 + 1.5 is bracketed as ((5 - ((3 / 2) * 4)) + ((6 * -2) / -3)) + 1.5. For each of the expressions in the previous exercise, write the expression with its brackets.

3.6 Strings, Characters, and their Operations

In Chapter 2 we noted that a textual phrase enclosed in double quotes, e.g., "hello", is a string. Like numbers and booleans, strings are values that can be computed upon and saved in variables. Java's data-type name for strings is String (note the upper-case S); here is an example:

String name = "Fred Mertz";

Literal strings can contain nonletters, such as blanks, numerals, tabs, and backspaces; here are examples:

• " " (all blanks)
• "1+2" (two numerals and a plus symbol---not an addition!)
• "" (an empty string)
• "!?,.\t\b\'\"\n\r\\" (four punctuation symbols, followed by
  • a tab (\t),
  • a backspace (\b),
  • a single quote (\'),
  • a double quote (\"),
  • a newline (\n),
  • a return (\r),
  • and a backslash (\\))

System.out.println("!?,.\t\b\'\"\n\r\\");

!?,.   '"
\

As we saw earlier in this chapter, the + operator computes on two strings by concatenating (appending) them together:

System.out.println("My name is " + name);

System.out.println("My name is R2D" + (5 - 3));

Integers and doubles are different from strings---you can multiply and divide with integers like 49 and 7 but you cannot do arithmetic on the the strings "49" and "7". Indeed, "49" + "7" computes to "497", because the + symbol represents concatenation when a string argument is used.

Later in this Chapter, we will learn techniques that transform numbers into strings and strings into numbers; these techniques will be necessary for an application to accept input data from a human user and do numerical computation on it.

The String type owns a rich family of operations, and we present several of them here. The operations for strings have syntax different from the arithmetic and comparison operators previously seen because strings are actually objects in Java, and the operations for strings are actually methods. For this reason, the following examples should be carefully studied:

• To compare two strings S1 and S2 to see if they hold the same sequence of characters, write

  S1.equals(S2)
  

  For example, "hello".equals("hel"+"lo") returns the boolean answer, true, whereas "hello".equals("Hello") results in false.

  Of course, the method can be used with a string that is named by a variable:

  String s = "hello";
  System.out.println(s.equals("hel"+"lo"));
  System.out.println(s.equals(s));
  

  prints true on both occasions.
• To determine a string's length, use the length() method: for string S, the message

  S.length()
  

  returns the integer length of the string, e.g.,

  String s = "ab";
  int i = s.length();
  

  assigns 2 to i.
• For string, S, S.trim() computes a new string that looks like string S but without any leading or trailing blanks. For example,

  String s = " ab c  ";
  String t = s.trim();
  

  assigns "ab c" to t---both the leading and trailing blanks are removed.

These methods and many others are listed in Table 5.

TABLE 5: methods on strings==========================================

ENDTABLE=============================================================

Finally, a warning: Do not use the == operation to compare strings for equality! For reasons that cannot be explained properly until a later chapter, the expression S1 == S2 does not validate that strings S1 and S2 contain the same sequence of characters; instead, it checks whether S1 and S2 are the same identical object. The proper expression to check equality of two strings is S1.equals(S2).

Characters

The individual symbols within a string are called characters, and the data type of characters is char. A character can be represented by itself by placing single quotes around it, e.g, 'W', 'a', '2', '&', etc.

We noted earlier symbols like the tab and backspace keys have special codings:

• \b (backspace)
• \t (tab)
• \n (newline)
• \r (return)
• \" (doublequote)
• \' (single quote)
• \\ (backslash)

char backspace = '\b';

Java uses the Unicode format for characters; inside the computer, characters are actually integers and you can do arithmetic on them, e.g., 'a'+1 converts (casts) 'a' into its integer coding, 97, and adds 1.

Begin Footnote: Indeed, it is possible to cast an integer into a printable character: If one writes (char)('a'+1), this casts the result of the addition into the character, 'b'---the phrase, (char) is the cast, and it forces the numeric value to become a character value. End Footnote.

To examine a a specific character within a string, use the charAt(i) method from Table 5, where i is a nonnegative integer. (Important: The characters within a string, S, are indexed by the position numbers 0, 1, ..., S.length()-1.) Examples are:

• char c = "abc".charAt(0)
  

  which saves character 'a' in variable c's cell.

• String s = "abc" + "de";
  char c = s.charAt(2+1);
  

  which saves 'd' in c's cell.

• "abc".charAt(3)
  

  which results in an error that stops execution, because there is no character number 3 in "abc".

boolean result =  s.charAt(0) == 'a';

Exercises

1. Calculate the results of these expressions:
   1. 2 + ("a" + " ") + "bc"
   2. 1 + "" + 2 + 3
   3. 1 + 2 + "" + 3
   4. 1 + 2 + 3 + ""
   5. 1 + "" + (2 + 3)
2. Here are two strings:

   String t = "abc ";
   String u = "ab";
   

   What is printed by these statements?
   1. System.out.println(t.equals(u));
   2. System.out.println(u.charAt(1) == t.charAt(1));
   3. System.out.println(t.length() - u.length());
   4. System.out.println(u + 'c');
   5. System.out.println(t.trim());
   6. System.out.println(t.toUpperCase());

3.7 Data-Type Checking

boolean b = true;
System.out.println(b * 5);

A data type is a ``species'' of value, much like horses, lions, and giraffes are species of animals. Trouble can arise when different species mix, and for this reason, the Java compiler uses data types to monitor usage of values and variables for compatibility. More generally, data types are useful because

• They ensure compatibility of operands to operators, e.g., 1 * 2.3 is an acceptable expression but "abc" * 2.3 is not.
• They predict a property about the result of an expression, e.g., whatever the result of 1 * 2.3 might be, it is guaranteed to be a double value.
• They help create variable cells of the appropriate format, e.g., double d declares a cell that is suited to hold only doubles.
• They help enfore compatibilities of expressions to variables in assignments, e.g., d = 1 * 2.3 is an acceptable assignment, because it places a double into a cell declared to hold only doubles.

We can list the steps the Java compiler takes to type-check an expression; consider these two variables and the arithmetic expression that uses them:

int i = 1;
double d = 2.5;
 ... ((-3 * i) + d) > 6.1 ...

The process continues: Since -3 * i has type int, but d has type double, this implies that the left operand will be automatically cast into a double and that the answer for (-3 * i) + 2, must be a double. Finally, the less-than comparison will produce a value that has type boolean.

The process outlined in the previous paragraph is sometimes drawn as a tree, as in Figure 6.

FIGURE 6: data-type tree for an arithmetic expression====================



ENDFIGURE=================================================================

The notion of data type extends to objects, too---the Java compiler uses the name of the class from which the object was constructed as the object's data type. For example, in Figure 4 of Chapter 2 we wrote

GregorianCalendar c = new GregorianCalendar();

System.out.println(c.getTime());

c.println("oops");

In summary, there are two forms of data types in the Java language:

• primitive types, such as int, double, and boolean
• reference (object) types, such as GregorianCalendar

Surprisingly, type String is a reference type in Java, which means that strings are in fact objects! This is the reason why the string operations in Table 5 are written as if they were messages sent to objects---they are!

Exercises

1. Without calculating the answers to these expressions, predict the data type of each expression's answer (or whether there is a data-type error):
   1. 5.3 + (7 / 2)
   2. 3 * (1 == 2)
   3. 1 < 2 < 3
   4. "a " + 1 + 2
   5. ("a " + 1) * 2
2. Which of these statements contain data type errors?

   int x = 3.5;
   double d = 2;
   String s = d;
   d = (d > 0.5);
   System.out.println(s * 3);
   

3.8 Input via Program Arguments

The applications in this chapter are a bit unsatisfactory, because each time we want to reuse a program, we must reedit it and change the values in the program's variable initialization statements. For example, if we wish to convert several temperatures from Celsius to Fahrenheit, then for each temperature conversion, we must reedit the program in Figure 4, recompile it, and restart it.

It would be far better to write the temperature conversion application just once, compile it just once, and let its user start the application again and again with different numbers for degrees Celsius. To achieve this, we make the application read a numeric temperature as input data each time it starts.

Java uses program arguments (also known as command-line arguments) as one simple way to supply input data to an application.

Begin Footnote: In the next Chapter, we learn a more convenient method for supplying input data. End Footnote

When she starts an application, the user types the program arguments---these are the inputs. The application grabs the program arguments and assigns them to internal variables.

Say that we have rewritten the temperature conversion program in Figure 4 to use program arguments:

• If you installed the JDK, then when you start an application, you type the program argument on the same line as the startup command, that is, you type

  java CelsiusToFahrenheit 20
  

  if you want to convert 20 Celsius to Fahrenheit.
• If you use an IDE to execute applications, you type the program argument in the IDE's field labelled ``Program Arguments,'' ``Arguments,'' or ``Command-Line Parameters.'' (See Figure 7.) Then you start the application.

FIGURE 7: Supplying a program argument to an IDE=========================



ENDFIGURE==================================================================

Before we develop the temperature-conversion application, we consider a simpler example that uses a program argument; perhaps we write an application, called LengthOfName, that accepts a person's name as its input data and prints the name's length in immediate response:

java LengthOfName "Fred Mertz"
The name, Fred Mertz, has length 10.

/** LengthOfName prints the length of its input program argument */
public class LengthOfName
{ public static void main(String[] args)
  { String name = args[0];   // the program argument is held in  args[0]
    int length = name.length();
    System.out.println("The name, " + name + ", has length " + length);
  }
}

In general, there can be no program arguments at all or multiple arguments. In the former case, nothing special needs to be done; in the latter, the arguments are written next to each other, separated by spaces, e.g.,

java ThisApplicationUsesFourArguments Fred Mertz 40 -3.14159

When the application is started, args[0] holds the string, "Fred", args[1] holds the string, "Mertz", args[2] holds the string, "40", and args[3] holds the string, "-3.14159"---all the program arguments become strings, whether they are surrounded by double quotes or not!

Why are args[2] and args[3] in the example holding strings and not numbers? The answer lies within the phrase, String[] args, which appears in method main's header line: This defines the name, args, for the variables that grab the program arguments, and the data type, String, which we must use with every main method, forces every program argument to become a string.

Begin Footnote: In Chapter 5 we learn that args is an example of a parameter, and in Chapter 8 we learn that args is an array. But we do not need the explanations of these concepts here to use program arguments. EndFootnote

Therefore, an application that relies on numbers for inputs must construct the numbers from the strings it reads as the program arguments. We now see how to do this.

3.8.1 Converting between Strings and Numbers and Formatting

Converting Strings into Integers and Doubles

The Java designers have written class Integer, from which we can construct an object that knows how to translate a string of numerals into an integer. (At this point, you should review the example in Figures 3 and 4, Chapter 2, that used class GregorianCalendar to create a similar ``helper'' object.)

Say that S is a string of numerals that we wish to translate into the corresponding integer, e.g.,

String S = "20";

• Create a new Integer object, by saying

  new Integer(S)
  

  The keyword, new, creates an object from class Integer. The object grabs the value of the argument (in this case, the value of S is "20"), saves it inside itself, and calculates its integer translation.
• Send the new object an intValue message. This can be done in two statements, e.g.,

  Integer convertor = new Integer(S);
  int c = convertor.intValue();
  

  or in just one:

  int c = new Integer(S).intValue();
  

  The message asks the object to return the integer translation. The integer---here, 20---is returned as the answer and is assigned to c.

In addition to class Integer, there is class Double, which creates objects that convert strings of numerals and decimals into double values, e.g.,

String approx_pi = "3.14159";
double d = new Double(approx_pi).doubleValue();

Begin Footnote: Both class Integer and class Double are located in the Java package, java.lang. Although it is acceptable to add the statement, import java.lang.* to the beginning of an application that uses the classes, the Java interpreter will automatically search java.lang when it tries to locate a class; hence, import java.lang.* is an optional statement and will not be used here. End Footnote

Converting a Number into a String and Formatting it for Printing

Converting a number into a string is simple: Because the operator, +, will combine a number and a string, we can concatenate an empty string to a number to ``convert'' it to a string:

double d = 68.8;
String s = d + "";

When printing a double, we often wish to present it in a fixed decimal format. For example,

System.out.println ("$" + (100.0/3.0));

$33.333333333333336

There is yet another class, named DecimalFormat, that constructs objects that know how to format doubles in a fixed decimal format:

• Because the class is located in the package, java.text, include

  import java.text.*;
  

  at the beginning of the application.
• Construct a DecimalFormat object as follows:

  new DecimalFormat(PATTERN)
  

  where PATTERN is a string that specifies the significant digits to the left and right of the decimal point. For example, the pattern, "0.00", in new DecimalFormat("0.00") states that there must be at least one digit to the left of the decimal point and there must be exactly two digits to the right of the decimal point. (The rightmost fractional digit is rounded.)

  Other patterns, e.g., ".000" or "00.0" are acceptable, and you may consult the Java API specification for class DecimalFormat for a full description of the legal patterns.

• Send a format(D) message to the object, where D is a double value, e.g.,

  DecimalFormat formatter = new DecimalFormat("0.00");
  double d = 100.0 / 3.0;
  String s = formatter.format(d);
  

  The format method returns the formatted string representation of its double argument, d; the previous statements place the string, 33.33, in s's cell.

Here are the steps presented together:

import java.text.*;
public class Test
{ public static void main(String[] args)
  {  ...
    DecimalFormat formatter = new DecimalFormat("0.00");
    double money = 100.0/3.0;
    System.out.println ("$" + formatter.format(money));
     ...
  }
}

3.8.2 Temperature Conversion with Input

We use the techniques from the previous section to make the temperature conversion application from Figure 4 read a Celsuis temperature as its input and display its translation to Fahrenheit. The input temperature will be a program argument that is supplied at the startup command, e.g.,

java CelsiusToFahrenheit 20

int c = new Integer(args[0]).intValue();

Next, we compute the result and format it as a decimal with exactly one fractional digit:

double f = ((9.0/5.0) * c) + 32;
DecimalFormat formatter = new DecimalFormat("0.0");
System.out.println("Degrees Fahrenheit = " + formatter.format(f));

FIGURE 8: application using a program argument=============================

import java.text.*;
/**  CelsiusToFahrenheit converts an input Celsius value to Fahrenheit.
  *    input: the degrees Celsius, a program argument, an integer
  *    output: the degrees Fahrenheit, a double */
public class CelsiusToFahrenheit
{ public static void main(String[] args)
  { int c = new Integer(args[0]).intValue(); // args[0] is the program argument
    double f = ((9.0/5.0) * c) + 32; 
    System.out.println("For Celsius degrees " + c + ",");
    DecimalFormat formatter = new DecimalFormat("0.0");
    System.out.println("Degrees Fahrenheit = " + formatter.format(f)); 
  }
}

ENDFIGURE================================================================

The program in Figure 8 can be used as often as we like, to convert as many temperatures as we like:

java CelsiusToFahrenheit 20

java CelsiusToFahrenheit 22

java CelsiusToFahrenheit -10

An Execution Trace of Temperature Conversion

The concepts related to program arguments are important enough that we must analyze them in detail with an execution trace. Say that the user starts the application in Figure 8 with the program argument, 20, which the Java interpreter reads as the string, "20".

A CelsiusToFahrenheit object is created in computer storage, and its execution starts at the first statement of its main method:

The first statement creates a cell named c; initially, there is no integer in it:

Next, execution of the statements in main pauses while object a1 receives the message, intValue(), and executes the requested method:

Exercises

1. Compile and execute Figure 8 three times with the program arguments 20, 22, and -10, respectively.
2. Revise the change-making program in Figure 3 so that the dollars and cents values are supplied as program arguments, e.g.,

   java MakeChange 3 46
   

3. Revise either or both of the programs, CelsiusToFahrenheit and KilometersToMiles, that you wrote as solutions to the preceding Exercises set, ``Arithmetic with Fractions: Doubles,'' so that the programs use program arguments.
4. Say that a program, Test, is started with the program arguments 12 345 6 7.89. Write initialization statements that read the arguments and place the string "12" into a variable, s; place the integer 6 into a variable, i; place the double 7.89 into a variable, d.
5. Write a sequence of three statements that do the following: reads a program argument as an integer, i; reads a program argument as an integer, j; prints true or false depending on whether i's value i s greater than j's.
6. Exercise 3 of the section, ``Named Quantities: Variables,'' had difficulties printing correctly formatted answers when the dollars-cents amount printed contained a cents amount less than 10. Use class DecimalFormat to solve this problem. Test your solution with the inputs of four quarters, one nickel and one penny.

3.9 Diagnosing Errors in Expressions and Variables

• Errors related to spelling, grammar, and context (data types), that the Java compiler detects. These are called compile-time errors.
• Errors that occur when the program executes, and a statement computes a bad result that halts execution prematurely. These are called run-time errors or exceptions.

As we noted in the previous Chapter, the Java compiler performs a thorough job of checking spelling and grammar. For example, perhaps Line 4 of our program was written

System.out.println( (1+2(*3 );

Test.java:4: ')' expected.
   System.out.println( (1+2(*3 );
                           ^

When using variables, take care with their declarations; one common error is misspelling the data-type name, String:

Test1.java:5: Class string not found in type declaration.
   string s;
   ^

With the inclusion of arithmetic expressions, a new form of error, a data-type error, can appear. For example, the statement,

System.out.println(3 + true);

Test.java:4: Incompatible type for +. Can't convert boolean to int.
   System.out.println(3 + true);
                        ^

Data-type errors also arise if a programmer attempts to save a value of incorrect type in a variable, e.g.,

int i = true;

System.out.println(i * 2);

A related issue is whether a variable holds any value at all; consider this example:

int i;
System.out.println(i * 2);

Yet another variable-related error is the declaration of one name in two declarations:

int a = 1;
double a = 2.5;
System.out.println(a);  // which  a?

The previous diagnoses by the compiler are a great help, because they prevent disasters that would arise if the program was executed. Unfortunately, the Java compiler cannot detect all errors in advance of execution. For example, divison by zero is a disaster, and it is hidden within this sequence of statements:

int i = 0;
System.out.println(1 / i);

java.lang.ArithmeticException: / by zero
        at Test.main(Test.java:4)

The above example of an exception is a bit contrived, but exceptions readily arise when a program's user types incorrect input information as a program argument. Consider this program sequence:

int i = new Integer(args[0]).intValue();
System.out.println(1 / i);

java.lang.NumberFormatException: abc
        at java.lang.Integer.parseInt(Integer.java)
        at java.lang.Integer.(Integer.java)
        at Test.main(Test.java:4)

Finally, some errors will not be identified by either the Java compiler and interpreter. For example, perhaps you wish to print whether the values held by variables x and y are the same, and you write:

int x = 3;
int y = 7;
System.out.println(x = y);

The reason for this surprising behavior is that x = y is an assignment and not a test for equality (x == y). The statement, System.out.println(x = y), assigns y's value to x's cell and then prints it. For historical reasons, the Java compiler allows assignments to appear where arithmetic expressions are expected, and results like the one seen here are the consequence. Remember to use == for equality comparisons.

3.10 Java Keywords and Identifiers

Identifiers are used to name variables, of course, but they are used for naming classes and methods also, e.g., Total and println are also identifiers and must be spelled appropriately. For consistent style, classes are named by identifiers that begin with an upper-case letter, whereas method names and variable names are named by identifiers that begin with lower-case letters.

Java's keywords have special meaning to the Java compiler and cannot be used as identifiers. Here is the list of keywords: abstract boolean break byte case cast catch char class const continue default do double else extends final finally float for future generic goto if implements import inner instanceof int interface long native new null operator outer package private protected public rest return short static super switch synchronized this throw throws transient try var void volatile while

3.11 Summary

Here is a listing of the main topics covered in this chapter:

New Constructions

• variable declaration (from Figure 1):

  int quarters = 5;
  

• arithmetic operators (from Figure 1):

  System.out.println( (quarters * 25) + (dimes * 10)
                       + (nickels * 5) + (pennies * 1) );
  

• assignment statement (from Figure 2):

  money = money % 25;
  

• data types (from Figure 4):

  int c = 22;  
  double f = ((9.0/5.0) * c) + 32;
  

• program argument (from Figure 6):

  int c = new Integer(args[0]).intValue();
  

New Terminology

• operator: a symbol, like * or -, that denotes an arithmetic operation
• operand: an argument to an operator, e.g., i in 3 + i.
• data type: a named collection, or ``species'' of values. In Java, there are two forms, primitive types, like int, double, and boolean, and reference types, like GregorianCalendar and DecimalFormat.
• variable: a cell that holds a stored primitive value (like an integer) or an address of an object.
• referencing a variable: fetching a copy of the value saved in a variable
• declaration: the statement form that constructs a variable
• initialization: the statement that gives a variable its first, initial value.
• assignment: the statement form that inserts a new value into a variable
• program argument: input data that is supplied to a Java application at startup, typically by typing it with the startup command.
• compile-time error: an error that is identified by the Java compiler
• run-time error (exception): an error that is identified by the Java interpreter, that is, when the application is executing.

Points to Remember

• The Java language lets you calculate on numbers, booleans, strings, and even objects. These values are organized into collections---data types---so that the Java compiler can use the types to monitor consistent use of variables and values in a program.
• Input data that is supplied by means of program arguments are accepted as strings and are saved in the variables, args[0], args[1], and so on, in the main method.
• Strings can be converted into numbers, if needed, by means of objects created from class Integer and class Double.

New Classes for Later Use

• class Integer. Converts strings of numerals into integers; has method intValue(), which returns the integer value of the string argument, S, in new Integer(S). See Figure 6.
• class Double. Converts strings of numerals into integers; has method doubleValue(), which returns the double value of the string argument, S, in new Double(S).
• String. Used like a primitive data type, but it is actually a class; see Table 5 for an extensive list of operations (methods).
• class DecimalFormat. Found in package java.text. Has the method, format(D), which returns the decimal-formatted value of double, D, based on the pattern, P, used in new DecimalFormat(P). See Figure 8.

3.12 Programming Projects

1. One ounce equals 28.35 grams. Use this equivalence to write an application that converts a value in ounces to one in grams; an application the converts a value in kilograms to one in pounds. (Recall that one kilogram is 1000 grams, and one pound is 16 ounces.)
2. One inch equals 2.54 centimeters. Use this equivalence to write the following applications:
   1. One that converts an input of feet to an output of meters; one that converts meters to feet. (Note: one foot contains 12 inchs; one meter contains 100 centimeters.)
   2. One that converts miles to kilometers; one that converts kilometers to miles. (Note: one mile contains 5280 feet; one kilometer contains 1000 meters.)
   3. The standard formula for converting kilometers to miles is 1 kilometer = 0.62137 miles. Compare the results from the application you just wrote to the results you obtain from this formula.
3. Write an application that reads four doubles as its input. The program then displays as its output the maximum integer of the four, the minimum integer of the four, and the average of the four doubles. (Hint: the Java method Math.max (resp., Math.min) will return the maximum (resp., minimum) of two doubles, e.g., Math.max(3.2, -4.0) computes 3.2 as its answer.)
4. The two roots of the quadratic equation ax² + bx + c = 0 (where a, x, b, and c are doubles) are defined

   
        -b + \/ b2 - 4ac                -b - \/ b2 - 4ac
   x =  ------------------    and  x =  -------------------
              2a                               2a
   
   

   Write an application that computes these roots from program arguments for a, b, and c. (Hint: the square root of E is coded in Java as Math.sqrt(E).)
5. 1. The compounded total of a principal, p (double), at annual interest rate, i (double), for n (int) years is

      total = p(( 1 + i ) )n)
      

      Write an application computes the compounded total based on program arguments for p, i, and n. (Hint: the power expression, a^b, is coded in Java as Math.pow(a,b).)
   2. Rewrite the above equation so that it solves for the value of p, thereby calculating the amount of starting principal needed to reach total in n years at annual interest rate i. Write an application to calculate this amount.
   3. Rewrite the above equation so that it solves for the value of i, thereby calculating the interest rate (the so-called discount rate) needed to reach a desired total starting at p and taking y years. Write an application to calculate this interest rate.
6. 1. The annual payment on a loan of principal, p (double), at annual interest rate, i (double), for a loan of duration of y (int) years is

      
                   (1 + i)y *p*i
      payment =  -----------------
                   (1 + i)y - 1
      
      

      Write an application that computes this formula for the appropriate program arguments. (Hint: the power expression, a^b, is coded in Java as Math.pow(a,b).)
   2. Given the above formula, one can calculate the amount of debt remaining on a loan after n years of payments by means of this formula:

      
                                                     zn - 1
      debt = (p * zn)  -  ( payment *  ------- )
                                                     z - 1 
      
      

      where z = 1 + i, and payment is defined in the previous exercise.

      Extend the application in the previous exercise so that it also prints the remaining debt for the Years 0 through 5 of the calculated loan.

7. 1. Starting with a principal, p, the total amount of money accumulated after contributing c each year for y years, assuming an annual interest rate of i, goes as follows:

      
                                  (1+i)y+1 - (1+i)
      total = (p * (1+i)y) + (c*( ----------------- )
                                        i
      
      

      Write an application that computes total for the four input values.
   2. Given a total amount money saved, total, the annual annuity payment that can be paid out every year for a total of z years, and still retain a nonnegative balance, is

      
                        total * (1+i)z-1 * i
      annual_payment = ----------------------
                         (1+i)z - 1
      
      

      assuming i is the annual interest that is paid into the remaining money. Write an application that computes the formula given the three inputs.
8. The acceleration of an automobile is the rate of change of its velocity. The formula for computing acceleration is

   
                   Vf - Vi
   acceleration = -----------
                      t
   
   

   where V_i is the automobile's initial velocity, V_f is its finial velocity, and t is the elapsed time the vehicle took, starting from V_i, to reach V_f. (Note: to use the formula, the measures of velocity and time must be consistent, that is, if velocities are expressed in miles per hour, then time must be expressed in hours. The resulting accleration will be in terms of miles and hours.)
   1. Write an application that computes acceleration based on input arguments for V_i, V_f, and t.
   2. Write an application that computes the time needed for an automobile to reach a final velocity from a standing start, given as input value of the acceleration.
   3. Write an application that computes the final velocity an automobile reaches, given a standing start and input values of time and acceleration.
9. Say that an automobile is travelling at an acceleration, a. If the automobile's initial velocity is V_i, then the total distance that the automobile travels in time t is

   distance = Vit + (1/2)a(t2)
   

   (Again, the measures of values must be consistent: If velocity is stated in terms of miles per hour, then time must be stated in hours, and distance will be computed in miles.) Use this formula to write the following applications:
   1. The user supplies values for V_i, a, and t, and the application prints the value of distance.
   2. The user supplies values only for V_i and a, and the application prints the values of distance for times 0, 1, 2, ... 10.
   3. Assuming that an automobile must begin from a stationary start, the user supplies a value only for a, and the application prints the values of distance for times, 0, 1, 2, ... 10.
10. Write an application, CountTheSeconds, that converts an elapsed time in seconds into the total number of days, hours, minutes, and leftover seconds contained in the time. For example, when the user submits an input of 289932, the program replies

    289932 is
    3 days,
    8 hours,
    32 minutes, and
    12 seconds
    

11. Write an application, DecimalToBinary, that translates numbers into their binary representations. The program's input is a program argument in the range of 0 to 63. For example, when the user types an input of 22, the program replies:

    22 in binary is 010110
    

    (Hint: Study the change-making program for inspiration, and use System.out.print to print one symbol of the answer at a time.)
12. Number theory tells us that a number is divisible by 9 (that is, has remainder 0) exactly when the sum of its digits is divisible by 9. (For example, 1234567080 is divisible by 9 because the sum of its digits is 36.)

    Write an application that accepts an integer in the range -99,999 to 99,999 as its input and prints as its output the sum of the integer's digits and whether or not the integer is divisible by 9. The output might read as follows:

    For input 12345,
    the sum of its digits is 15.
    Divisible by 9?  false
    

13. In the Math object in java.lang there is a method named random: using Math.random() produces a (pseudo-)random double that is 0.0 or larger and less than 1.0. Use this method to write a program that receives as input an integer, n, and prints as its output a random integer number that falls within the range of 0 to n.
14. Next, use Math.random() to modify the CelsiusToFahrenheit application in Figure 4 so that it each time it is started, it chooses a random Celsius temperature between 0 and 40 and prints its conversion, e.g.,

    Did you know that 33 degrees Celsuis
    is 91.4 degrees Fahrenheit?
    

15. Write an application, Powers, that takes as its input an integer, n and prints as output n's powers from 0 to 10, that is, n⁰, n¹, n², ..., n¹⁰.
16. Write an application, PrimeTest, that takes as its input an integer and prints out which primes less than 10 divide the integer. For example, for the input:

    java PrimeTest 28
    

    The program replies

    2 divides 28? true
    3 divides 28? false
    5 divides 28? false
    7 divides 28? true
    

17. Write an application that computes a worker's weekly net pay. The inputs are the worker's name, hours worked for the week, and hourly payrate. The output is the worker's name and pay. The pay is computed as follows:
    • gross pay is hours worked multiplied by payrate. A bonus of 50% is paid for each hour over 40 that was worked.
    • a payroll tax of 22% is deducted from the gross pay.
18. Write an application that computes the cost of a telephone call. The inputs are the time the call was placed (this should be written as a 24-hour time, e.g., 2149 for a call placed a 9:49p.m.), the duration of the call in minutes, and the distance in miles of the destination of the call. The output is the cost of the call. Cost is computed as follows:
    • Basic cost is $0.003 per minute per mile.
    • Calls placed between 8am and midnight (800 to 2400) are subject to a 20% surcharge. (That is, basic cost is increased by 0.2.)
    • A tax of 6% is added to the cost.
    The difficult part of this project is computing the surcharge, if any. To help do this, use the operation Math.ceil(E), which returns the nearest integer value that is not less than E. For example, Math.ceil(0.2359 - 0.0759) equals 1.0, but Math.ceil(0.0630 - 0.0759) equals 0.0.

3.13 Beyond the Basics

3.13.1 Longs, Bytes, and Floats

Almost all the computations in this text rely on just integers, doubles, booleans, and strings. But the Java language possesses several other primitive data types, and we survey them here.

The data type int includes only those whole numbers that can be binary coded in a single storage word of 32 bits---that is, numbers that fall in the range of -2 billion to 2 billion (more precisely, between -2³¹ and (2³¹)-1). To work with integers that fall outside this range, we must use long integers. (The data type is long.) Create a long integer by writing a number followed by an L, e.g., 3000000000L is a long 3 billion. Long variables are declared in the standard way, e.g.,

long x = 3000000000L;

Longs are needed because answers that fall outside the range of the int type are unpredictable. For example, write a Java program to compute 2000000000 + 1000000000 and compare the result to 2000000000L + 1000000000L The former overflows, because the answer is too large to be an integer, and the result is nonsensical. If you plan to work with numbers that grow large, it is best to work with longs.

At the opposite end of the spectrum is the byte data type, which consists of those ``small'' integers in the range -128 to 127, that is, those integers that can be represented inside the computer in just one byte---eight bits---of space. For example, 75 appears inside the computer as the byte 01001011. (To make 75 a byte value, write (byte)75.) Byte variables look like this:

byte x = (byte)75;

Java also supports the data type float of fractional numbers with 8 digits of precision. A float is written as a fractional number followed by the letter, F. For example, 10.0F/3.0F calculates to 3.3333333. A double number can be truncated to 8 digits of precision by casting it to a float, e.g.,

double d = 10/3.0;
System.out.println( (float)d );

Floats can be written in exponential notation e.g.,

float x = 3e-4F;

TABLE 9: data types==============================================

ENDTABLE===========================================================

3.13.2 Helper Methods for Mathematics

TABLE 10: mathematical methods======================================

ENDTABLE=========================================================

3.13.3 Syntax and Semantics of Expressions and Variables

The syntax and semantics of expressions and variables are surprisingly rich, and we will reap rewards from investing some time in study. The starting point is the notion of ``data type'':

Data Type

TYPE ::=  PRIMITIVE_TYPE | REFERENCE_TYPE
PRIMITIVE_TYPE ::=  boolean | byte | int | long | char | float | double
REFERENCE_TYPE ::=  IDENTIFIER | TYPE[]

Semantics: In concept, a data type names a collection of related values, e.g., int names the collection of integer numbers. In practice, the Java compiler uses data types to monitor consistent use of variables and values; see the section, ``Data Type Checking'' for details.

Declaration

DECLARATION ::=  TYPE IDENTIFIER [[ = INITIAL_EXPRESSION ]]? ;

See the section, ``Java Keywords and Identifiers,'' for the syntax of Java identifiers.

Semantics: A declaration creates a cell, named by the identifier, to hold values of the indicated data type. The cell receives the value computed from the initial expression (if any).

Statement and Assignment

STATEMENT ::=  DECLARATION
              | STATEMENT_EXPRESSION ;
STATEMENT_EXPRESSION ::=  OBJECT_CONSTRUCTION | INVOCATION | ASSIGNMENT

ASSIGNMENT :=  VARIABLE = EXPRESSION
VARIABLE ::=  IDENTIFIER

Semantics: An assignment proceeds in three stages:

1. determine the cell named by the variable on the left-hand side of the equality;
2. calculate the value denoted by the expression on the right-hand side of the equality;
3. store the value into the cell.

Expression

EXPRESSION ::=  LITERAL
                | VARIABLE
                | EXPRESSION INFIX_OPERATOR EXPRESSION
                | PREFIX_OPERATOR EXPRESSION
                | ( EXPRESSION )
                | ( TYPE ) EXPRESSION
                | STATEMENT_EXPRESSION
LITERAL ::=  BOOLEAN_LITERAL
             | INTEGER_LITERAL | LONG_LITERAL
             | FLOAT_LITERAL | DOUBLE_LITERAL
             | CHAR_LITERAL | STRING_LITERAL
INFIX_OPERATOR ::=   +  |  -  |  *  |  /  |  %
                        |  <  |  >  |  <=  |  >=  |  ==  |  !=
PREFIX_OPERATOR ::=  -  
INITIAL_EXPRESSION ::=  EXPRESSION

Semantics: Evaluation of an expression proceeds from left to right, following the operator precedences set down in the section, ``Operator Precedences.''