
The order in which a program's statements execute is called its control flow. Of course, by writing statements in a sequential order and inserting method invocations, a programmer specifies a program's control flow. When a programmer writes statements in a sequential ordering,
STATEMENT1; STATEMENT2; ... STATEMENTn;this decides the control flow that STATEMENT1 executes first, followed by STATEMENT2 and so on. A method invocation,
RECEIVER.METHOD(ARGUMENTS);decides the control flow that execution pauses at the place of invocation so that the statements named by METHOD in RECEIVER execute next.
Sequencing and invocation are control structures because they order or ``structure'' a program's control flow. A programmer must develop intutitions about control flow, and the execution traces presented in previous chapters were intended to foster these intuitions.
One deficiency of the two control structures just seen is that they are unable to change the control flow based on the values of input data or the occurrence of errors. To remedy this limitation, we must learn a new control structure.
Real-life algorithms often contain instructions that take a course of action based on the answer to a question, for example,
The syntax of the conditional statement is
if ( TEST )
{ STATEMENTS1 }
else { STATEMENTS2 }
where the TEST is an expression that must evaluate
to a boolean-typed answer, that is,
true or false. (An example of such an expression
is 4 > (2 + 1), which computes to true;
see Chapter 3 for many other examples.) If TEST
evaluates to true, then STATEMENTS1 are executed
and statements S2 are ignored. If TEST
evaluates to false, STATEMENTS2 are
executed and STATEMENTS1
are ignored.
Here is a method that uses a conditional:
/** printPolarity prints whether its argument is negative or not.
* @param i - the argument */
public void printPolarity(int i)
{ System.out.print("The argument is ");
if ( i < 0 )
{ System.out.println("negative."); }
else { System.out.println("nonnegative."); }
System.out.println("Finished!");
}
The method cannot forecast the value of the argument sent to it,
so it uses a
conditional statement that asks a question about the argument.
If the method is invoked with, say, printPolarity(3 - 1),
the command window displays
The argument is nonnegative. Finished!which shows that the test, i < 0, evaluated to false and the statement labelled by else was executed. The conditional statement is written on several lines to aid readability; the statements preceding and following the conditional execute as usual.
In contrast, the invocation, printPolarity(-1), causes
The argument is negative. Finished!to print. This shows that the method chooses its computation based on the value of its actual parameter---there are two possible control flows through the method, and the appropriate control flow is selected when the method is invoked.
Some people like to visualize a conditional statement as a ``fork in the road'' in their program; they draw a picture of if ( TEST ) { STATEMENTS1 } else { STATEMENTS2 } like this:
The two paths fork apart and join together again, displaying the two possible control flows. The picture also inspires this terminology: We call statements STATEMENTS1 the then-arm and call statements STATEMENTS2 the else-arm. (Many programming languages write a conditional statement as if TEST then STATEMENTS1 else STATEMENTS2; the keyword, then, is omitted from the Java conditional but the terminology is preserved.)
Occasionally, only one plan of action is desired, and a conditional statement written as
if ( TEST )
{ STATEMENTS }
which
is an abbreviation of
if ( TEST ) { STATEMENTS } else { }.
An arm of a conditional statement can hold multiple statements, as we see in the application in Figure 1, which translates hours into seconds. The algorithm upon which the application is based is simple but significant, because it asks a question:
FIGURE 1: application that converts hours into seconds==================
import javax.swing.*;
/** ConvertHours translates a time in hours into its equivalent in seconds.
* Input: a nonnegative integer
* Output: the converted time into seconds. */
public class ConvertHours
{ public static void main(String[] args)
{ int hours = new Integer(
JOptionPane.showInputDialog("Type hours, an integer:")).intValue();
if ( hours >= 0 )
{ // at this point, hours is nonnegative, so compute seconds:
int seconds = hours * 60 * 60;
JOptionPane.showMessageDialog(null,
hours + " hours is " + seconds + " seconds");
}
else { // at this point, hours must be negative, an error:
JOptionPane.showMessageDialog(null,
"ConvertHours error: negative input " + hours);
}
}
}
ENDFIGURE================================================================
The application uses a conditional statement to ask the question whether the user typed an appropriate input value. The programmer can safely assume that the statements in the then-arm execute only when hours has a nonnegative value---the if-statement's test provides a precondition that ``guards'' entry of control flow into the then-arm.
The then-arm consists of two statements, showing that sequential control can ``nest'' within conditional control. Further, one of the statements sends a message, showing that invocation control can nest within conditional control. It is sensible for conditional control to nest within conditional control as well, as we see in the next section.
double d = 4.14;
int i = 3;
if ( i == d )
{ System.out.println("Equal"); }
else { i = (int)d; }
if ( i != 3 )
{ System.out.println("Not equal"); }
public static void main(String[] args)
{ System.out.println( f(2, 3) );
int i = 2;
System.out.println( f(i+1, i) );
}
private static String f(int x, int y)
{ String answer;
if ( x <= y )
{ answer = "less"; }
else { answer = "not less"; }
return answer;
}
/** printEven prints whether its argument is even or odd: * It prints "EVEN" when the argument is even. * It prints "ODD" when the argument is odd. * @param a - the argument */ public void printEven(int a)
/** minus subtracts its second argument from its first, provided that * the result is nonnegative * @param arg1 - the first argument, must be nonnegative * @param arg2 - the second argument * @return (arg1 - arg2), if arg1 >= arg2; * return -1, if arg1 is negative or if arg2 > arg1 */ public int minus(int arg1, int arg2)(Hint: place a conditional statement inside a conditional.)
/** div does integer division on its arguments * @param arg1 - the dividend * @param arg2 - the divisor * @return (arg1 / arg2), provided that arg2 is nonzero; * return 0 and print an error message, if arg2 == 0 */ public int div(int arg1, int arg2)
Perhaps we revise the change-making application from Chapter 3 so that it verifies that the dollars and cents inputs are reasonable: the dollars should be nonnegative and the cents should range between 0 and 99. If any of these conditions are violated, the computation of change making must not proceed.
This situation requires several questions to be asked and it requires that we nest the questions so that the change is computed only when all the questions are answered correctly. The algorithm for doing displays a nested structure:
FIGURE 2: change-making with nested conditionals========================
import javax.swing.*;
/** MakeChangeAgain calculates change in coins for a dollars, cents amount.
* Input: two numbers supplied at the command line:
* a dollars amount, a nonnegative integer;
* a cents amount, an integer between 0 and 99.
* Output: the coins */
public class MakeChangeAgain
{ public static void main(String[] args)
{ int dollars = new Integer(args[0]).intValue();
if ( dollars < 0 )
{ JOptionPane.showMessageDialog(null,
"MakeChangeAgain error: negative dollars: " + dollars);
}
else // dollars amount is acceptable, so process cents amount:
{ int cents = new Integer(args[1]).intValue();
if ( cents < 0 )
{ JOptionPane.showMessageDialog(null,
"MakeChangeAgain error: negative cents: " + cents);
}
else { if ( cents > 99 )
{ JOptionPane.showMessageDialog(null,
"MakeChangeAgain error: bad cents: " + cents);
}
else // dollars and cents are acceptable, so compute answer:
{ int money = (dollars * 100) + cents;
System.out.println("quarters = " + (money / 25));
money = money % 25;
System.out.println("dimes = " + (money / 10));
money = money % 10;
System.out.println("nickels = " + (money / 5));
money = money % 5;
System.out.println("pennies = " + money);
}
}
}
}
}
ENDFIGURE===============================================================
Each question is expressed in a conditional statement, and
the nested is reflected by the indentation of the statements.
Brackets are aligned to help us see the control structure.
When writing algorithms like the one for change making, some programmers like to sketch a picture of the questions and the possible control flows. The picture, called a flow chart, can prove helpful when there are numerous questions to ask and the dependencies of the questions are initially unclear. Figure 3 shows the flowchart corresponding to the change-making algorithm.
FIGURE 3: flowchart for change making==============================From the flowchart, one can calculate the possible control flows and consider what input data values would cause execution of each flow; this is useful for testing the method. (See the Exercises below and the Section on testing at the end of this Chapter.)ENDFIGURE==============================================================
One disadvantage of nested conditionals is difficult readability---when reading a statement in the middle of nested conditionals, a programmer can quickly forget which questions led to the statement. For this reason, some programmers prefer to ``unnest'' the conditionals by inserting a boolean variable that remembers the answers to the conditionals' tests.
We can unnest the conditionals Figure 2 with this technique; see Figure 4.
FIGURE 4: unnesting conditional statements=============================
import javax.swing.*;
/** MakeChangeAgain calculates change in coins for a dollars, cents amount.
* Input: two numbers supplied at the command line:
* a dollars amount, a nonnegative integer;
* a cents amount, an integer between 0 and 99.
* Output: the coins */
public class MakeChangeAgain2
{ public static void main(String[] args)
{ boolean ok = true; // remembers whether input data is acceptable
int dollars = new Integer(args[0]).intValue();
int cents = new Integer(args[1]).intValue();
if ( dollars < 0 )
{ JOptionPane.showMessageDialog(null,
"MakeChangeAgain error: negative dollars: " + dollars);
ok = false; // the error negates acceptability
}
if ( ok )
// dollars are acceptable, so consider cents:
{ if ( cents < 0 )
{ JOptionPane.showMessageDialog(null,
"MakeChangeAgain error: negative cents: " + cents);
ok = false;
}
if ( cents > 99 )
{ JOptionPane.showMessageDialog(null,
"MakeChangeAgain error: bad cents: " + cents);
ok = false;
}
}
if ( ok )
// dollars and cents are acceptable, so compute answer:
{ int money = (dollars * 100) + cents;
System.out.println("quarters = " + (money / 25));
money = money % 25;
System.out.println("dimes = " + (money / 10));
money = money % 10;
System.out.println("nickels = " + (money / 5));
money = money % 5;
System.out.println("pennies = " + money);
}
}
}
ENDFIGURE=============================================================
The boolean, ok, remembers whether the input-checking tests
have been answered favorably. If so, calculation of change
executes. The conditionals are simplified into
if-then statements (there are no else-arms; recall that
if ( TEST ) { S } abbreviates
if ( TEST ) { S } else { }).
Nesting is greatly reduced, but
the formal relationship
between the original algorithm and the one implicit in Figure 4 is not
easy to state---by considering all control flows we can determine
whether the two applications behave exactly the same way.
int i = 1;
if ( i < 0 )
{ System.out.println("a"); }
else { System.out.println("b");
if ( i == 1 )
{ System.out.println("c"); }
System.out.println("d");
}
System.out.println("e");
/** convertToSeconds converts an hours, minutes amount into the * equivalent time in seconds. * @param hours - the hours, a nonnegative integer * @param minutes - the minutes, an integer in the range 0..59 * @return the time in seconds; in case of bad arguments, return -1 */ public int convertToSeconds(int hours, int minutes)
Java's form of conditional statement has a problematic syntax that allows serious errors to go undetected by the Java compiler.
For example, when an arm of a conditional is a single statement, it is legal to omit the brackets that enclose the arm. This can prove disastrous---say that we have this conversion method, and we forget the brackets around the else-arm:
public int convertHoursIntoSeconds(int hours)
{ int seconds;
if ( hours >= 0 )
{ int seconds = hours * 60 * 60; }
else JOptionPane.showMessageDialog(null, "error: returning 0 as answer");
seconds = 0;
return seconds;
}
Because of the missing brackets,
the Java compiler decides that the
else-arm is just one statement, and the compiler
inserts this bracketing:
if ( hours >= 0 )
{ int seconds = hours * 60 * 60; }
else { JOptionPane.showMessageDialog(null, "error: returning 0 as answer"); }
seconds = 0;
which is certainly not what was intended.
Just as bad is an accidental omission of the keyword, else. The missing else in the same example,
if ( hours >= 0 )
{ int seconds = hours * 60 * 60; }
{ JOptionPane.showMessageDialog(null, "error: returning 0 as answer");
seconds = 0;
}
is not noticed by the compiler, which assumes that the conditional
has only a then-arm. As a result, the statements following
the then-arm are always executed,
which is again incorrect.
Another problem that can arise when brackets are absent is the famous ``dangling else'' example. Consider this example, deliberately badly formatted to reveal no secrets:
if ( E1 ) if ( E2 ) S1 else S2After some thought, we can correctly conclude that the then-arm that mates to the test, if ( E1 ), is indeed the second conditional statement, if ( E2 ) S1, but an unresolved question is: Does else S2 belong to if ( E1 ) or if ( E2 )? The Java compiler adopts the traditional answer of associating the else-arm with the most recently occurring test, that is, else S2 mates with if ( E2 ). You should not rely on this style as a matter of course; the price of inserting brackets is small for the clarity gained.
Another undetected error occurs when an extra semicolon is inserted, say, just after the test expression. This statement from Figure 7 is altered to have an extra semicolon:
if ( minute < 10 );
{ answer = answer + "0"; }
Because of the semicolon, the compiler treats the conditional
as if it has no then- or else- arms! That is, the compiler
reads the above as follows:
if ( minute < 10 ) { } else { }
{ answer = answer + "0"; }
This makes the conditional worthless.
Once you are certain your conditional statement is correctly written, you should test it. Remember that a conditional statement contains two possible paths of execution and therefore should be tested at least twice, with one test that causes execution of the then-arm and one test that causes execution of the else-arm.
Sometimes we wish to insert two comparison operations within one test expression. For example, the change-making applications in Figures 2 and 4 would benefit from asking, ``cents < 0 or cents > 99''? as one question, rather than two.
To do so, we may use relational operations, which operate on boolean arguments and produce boolean answers. For example, the logical disjunction, ``or,'' is written in Java as the relational operation, ||, so we can state,
if ( (cents < 0) || cents > 99) )
{ JOptionPane.showMessageDialog(null,
"MakeChangeAgain error: bad cents: " + cents);
...
}
This statement's test calculates to true if the first
phrase, cents < 0, computes to true. If it
computes to false, then the second phrase is computed---if
cents > 99 computes to true then the test computes
to true. If both phrases compute to false, then
so does the test. In this way, two related questions can be efficiently
asked at the same point in the program.
In a similar manner, we might use logical ``and'' (conjunction) to write an expression that asks whether integer variable minutes falls in the range 0..59:
(minutes >= 0) && (minutes <= 59)The symbol, &&, denotes ``and.'' A small execution trace of this expression would be helpful; assume that minutes holds 64:
(minutes >= 0) && (minutes <= 59) => (64 >= 0) && (minutes <= 59) => true && (minutes <= 59) => true && (64 <= 59) => true && false => falseSince one of the arguments to && resulted in false, the test's result is false.
Table 5 lists the commonly used relational operations and their calculation rules.
TABLE 5: logical operations===========================================
| Operator | Semantics |
| E1 && E2 |
conjunction (``and''):
|
| E1 || E2 |
disjunction (``or''):
|
| !E |
negation(``not''):
|
ENDTABLE================================================================The semantics in the Table should be followed exactly as written; consider this example:
(2 != 1) || (x == 3.14) => true || (x == 3.14) => trueSince the first argument to the disjunction, ||, resulted in true, there is no need to compute the result of the second argument, so the answer for the expression is true.
We may write expressions with multiple relational operations, e.g.,
(x == 2) || (x == 3) || (x == 5) || (x == 7)asks whether integer x is a prime less than 10, and
(y >= 0) && (((y % 3) == 0) || (y < 3))asks whether integer y is nonnegative and is either a multiple of 3 or has value 0, 1, or 2. Also, a negation operator always inverts the result produced by its argument, e.g.,
!(cents >= 0 && cents <= 99)returns true exactly when cents's value falls outside the range 0..99. For example, say that cents is 12:
!(cents >= 0 && cents <= 99) => !(12 >= 0 && cents <= 99) => !(true && cents <= 99) => !(true && 12 <= 99) => !(true && true) => !true => false
Relational operations can be used to compress the nesting structure of conditionals. Indeed, if we study the flowchart in Figure 3, we notice that the three tests are used to determine whether to generate an error dialog or to compute change. We might be so bold as to combine all three tests into one with relational operations; see Figure 6 for the result, where less precise error reporting is traded for a simpler control structure.
FIGURE 6: change making with logical relational operations================
import javax.swing.*;
/** MakeChangeAgain calculates change in coins for a dollars, cents amount.
* Input: two numbers supplied at the command line:
* a dollars amount, a nonnegative integer;
* a cents amount, an integer between 0 and 99.
* Output: the coins */
public class MakeChangeAgain3
{ public static void main(String[] args)
{ int dollars = new Integer(args[0]).intValue();
int cents = new Integer(args[1]).intValue();
if ( (dollars < 0) || (cents < 0) || (cents > 99) )
{ JOptionPane.showMessageDialog(null,
"MakeChangeAgain error: bad inputs: " + dollars + " " + cents);
}
else // dollars and cents are acceptable, so compute answer:
{ int money = (dollars * 100) + cents;
System.out.println("quarters = " + (money / 25));
money = money % 25;
System.out.println("dimes = " + (money / 10));
money = money % 10;
System.out.println("nickels = " + (money / 5));
money = money % 5;
System.out.println("pennies = " + money);
}
}
}
ENDFIGURE===============================================================
Relational operations are evaluated after arithmetic operations and comparison operations, and for this reason, it is acceptable to omit some of the parentheses in the above example:
if ( dollars < 0 || cents < 0 || cents > 99 )
public int minus(int arg1, int arg2)
{ int answer;
if ( arg1 < 0 || arg2 > arg1 )
{ answer = -1; }
else { answer = arg1 - arg2; }
return answer;
}
what results are returned by minus(3, 2)?
minus(2, 3)? minus(-4, -5)?
minus(4, -5)?
/** isSmallPrime says whether is argument is a prime number less than 10 * @param i - the argument * @return true, if the argument is as prime less than 10; * return false, otherwise. */ public boolean isSmallPrime(int i)
/** divide does division on its two arguments * @param x - a nonnegative value * @param y - a value not equal to zero * @return (x / y), if the above conditions on x and y hold true; * return 0, otherwise. */ public double divide(double x, double y)
Two main uses of conditionals are
We desire a method, twelveHourClock, which converts a time from a twenty-four hour clock into the corresponding value on a twelve-hour clock. (For example, twelveHourClock(16,35) would return "4:35 p.m." as its result.) Such a method must be intelligent enough to understand ``a.m.'' and ``p.m.'' as well as defend itself against nonsensical arguments (e.g., twelveHourClock(-10,99)).
The algorithm for the method might go as follows:
FIGURE 7: method that uses conditionals to convert time==================
/** twelveHourClock converts a 24-hour-clock time into a 12-hour-clock time.
* @param hour - the hour time, in the range 0..23
* @param minute - the minutes time, in the range 0..59
* @return the 12-hour-clock time, formatted as a string. */
public String twelveHourClock(int hour, int minute)
{ String answer = ""; // accumulates the formatted time, symbol by symbol
if ( hour < 0 || hour > 23 || minute < 0 || minute > 59 )
{ answer = "twelveHourClock error: " + hour + "." + minute; }
else { if ( hour >= 13 ) // hours 13..23 are reduced by 12
{ answer = answer + (hour - 12); }
else { if ( hour == 0 ) // hour 0 is written as 12
{ answer = answer + "12"; }
else { answer = answer + hour; }
}
answer = answer + ":";
if ( minute < 10 ) // display minutes 0..9 as 00..09
{ answer = answer + "0"; }
answer = answer + minute;
if ( hour < 12 ) // morning or afternoon?
{ answer = answer + " a.m."; }
else { answer = answer + " p.m."; }
}
return answer;
}
ENDFIGURE============================================================
The first conditional examines the parameters for possible nonsensical
values.
(As stated in Table 1, || denotes ``or.'')
If the test computes to true, an error message is constructed.
Otherwise, the the function assembles the twelve-hour time, symbol by symbol, within the string variable, answer, as described by the algorithm we just studied. It is essential that the brackets for each conditional's arms be placed correctly, otherwise the method will behave improperly---it helps to align the matching brackets and indent the arms, as displayed in the Figure.
Figure 7 is fascinating because the nested conditional structures are essential to computing the correct result. Study the Figure until you understand every detail.
We finish with a second use of conditionals---responding to input dialogs. Recall that a Java input dialog presents the user with a text field for typing input, and two buttons:
When the user presses OK, the text entered into the text field is returned to the application that constructed the dialog. But if the user presses Cancel, the text is lost, and a special value, called null, is returned instead.
With the help of a conditional statement, we can check whether a user has pressed OK or Cancel on the dialog:
String input = JOptionPane.showInputDialog
("Type some input and press a button:");
if ( input == null ) // did the user press CANCEL?
{ ... take appropriate action to cancel the transaction ... }
else { ... process the input ... }
Here is an example that shows this technique:
We might insert the twelveHourClock method into
a class TimeConvertor and use it with a main method that
uses input dialogs.
The algorithm for main goes like this:
public static void main(String[] args)
{ TimeConvertor time = new TimeConvertor(); // holds the method in Figure 7
String input = JOptionPane.showInputDialog
("Type hours in range 0..23:");
if ( input == null ) // did the user press Cancel?
{ JOptionPane.showMessageDialog(null, "Request cancelled"); }
else { int hours = new Integer(input).intValue();
int minutes = 0;
input = JOptionPane.showInputDialog
("Type minutes in range 0..59:");
if ( input != null ) // did the user press OK?
{ minutes = new Integer(input).intValue(); }
String answer = time.twelveHourClock(hours, minutes);
JOptionPane.showMessageDialog(null, "Time is " + answer);
}
}
/** translateGrade converts a numerical score to a letter grade. * @param score - a numerical score that must be in the range 0..100 * @return a letter grade based on this scale: * 100..90 = "A"; 89..80 = "B"; 79..70 = "C"; 69..60 = "D"; 59..0 = "F" */ public String translateGrade(int score)Use the method in an application that asks the user to type a numerical score and prints the corresponding letter grade.
nickels = 1 pennies = 2
1 quarter 2 dimes 1 penny
In the usual case, you should not alter the normal control flow of conditionals, statement sequences, and method invocations---such alterations make it almost impossible for a programmer to calculate possible control flows and analyze a program's behavior. But there are rare cases, when a fatal error has occurred in the middle of a computation, where terminating the flow of control is tolerable. We briefly consider techniques for premature termination due to an error.
Even though it might be well written, a program can receive bad input data, for example, a sequence of letters might be received as input when a number was required:
int i = new Integer(args[0]).intValue();If the program's user enters abc as the program argument, the program will halt with this fatal error, and we say that an exception is thrown:
java.lang.NumberFormatException: abc
at java.lang.Integer.parseInt(Integer.java)
at java.lang.Integer.(Integer.java)
at Test.main(Test.java:4)
The message notes that the exception was triggered at Line 4
and that the origin of the error lays within the Integer
object created in that line.
Throwing an exception alters the usual control flow---the program stops execution at the program line where the exception arises, and control is ``thrown'' out of the program, generating the error message and terminating the program.
Exceptions are thrown when potentially fatal errors arise, making it too dangerous to continue with the expected flow of control. For example, integer i in the above example has no value if "abc" is the input, and it is foolish to proceed with execution in such a case. Here is another situation where a fatal error might arise:
/** convertHoursIntoSeconds converts an hours amount into seconds
* @param hours - a nonnegative int
* @return the quantity of seconds in hours */
public int convertHoursIntoSeconds(int hours)
{ int seconds = 0;
if ( hours < 0 )
{ JOptionPane.showMessageDialog(null,
"ConvertHours error: negative input " + hours);
// should control proceed?
}
else { seconds = hours * 60 * 60; }
return seconds;
}
Unfortunately, if this method is invoked with a negative actual
parameter, it returns an incorrect answer, meaning that the
then-arm of the conditional has failed in its goal of computing
the conversion of hours into seconds. This is potentially
disastrous, because the client object that invoked the method
will proceed with the wrong answer and almost certainly
generate more errors.
In such a situation, premature termination might be acceptable. A programmer can force an exception to be thrown by inserting a statement of this form:
throw new RuntimeException(ERROR_MESSAGE);where ERROR_MESSAGE is a string. The statement terminates the control flow and throws an exception, which prints on the display with the line number where the exception was thrown and the ERROR_MESSAGE. Figure 8 shows the method revised to throw an exception when the actual parameter is erroneous.
FIGURE 8: method with thrown exception=================================
/** convertHoursIntoSeconds converts an hours amount into seconds
* @param hours - a nonnegative int
* @return the quantity of seconds in hours */
public int convertHoursIntoSeconds(int hours)
{ int seconds = 0;
if ( hours < 0 )
{ String error = "convertHoursIntoSeconds error: bad hours " + hours;
JOptionPane.showMessageDialog(null, error);
throw new RuntimeException(error);
}
else { seconds = hours * 60 * 60; }
return seconds;
}
ENDFIGURE===============================================================
This technique should be used sparingly, as a last resort, because its usual effect is to terminate the application immediately.
It is possible for an application to prevent termination due to an exception by using a control structure called an exception handler. Exception handlers are easily overused, so we delay their study until Chapter 11.
System.exit(0);This statement does not generate an error message on the display, and like throwing exceptions, should be used sparingly.
public void printSeconds(int hours)
{ if ( hours < 0 )
{ return; }
int seconds = hours * 60 * 60;
System.out.println(hours + " is " + seconds + " seconds");
}
Java allows the return statement to be used without a
returned value when a method's header line's return type is void.
Second, here is a method that immediately returns a useless answer when an error arises:
public int convertToSeconds(int hours)
{ if ( hours < 0 )
{ return -1; }
int seconds = hours * 60 * 60;
return seconds;
}
This example shows that a method may possess multiple return
statements.
Premature returns can be easily abused as shortcuts for reducing nested conditionals, and you are encouraged to use relational operators for this purpose instead.
if ( i == 2 )
{ System.out.println("2"); }
else { if ( i == 5 )
{ System.out.println("5");
j = j + i;
}
else { if ( i == 7 )
{ System.out.println("7");
j = j - i;
}
else { System.out.println("none"); }
}
}
The nesting is annoying, because the nested conditional merely considers
three possible values of i.
Java provides a terser alternative to the nested if-else statements, called a switch statement. Here is the above example, rewritten with the switch:
switch ( i )
{ case 2: { System.out.println("2");
break;
}
case 5: { System.out.println("5");
j = j + i;
break;
}
case 7: { System.out.println("7");
j = j - i;
break;
}
default: { System.out.println("none"); }
}
The above switch statement behaves just like the nested
conditional.
The syntax we use for the switch statement is
switch ( EXPRESSION )
{ case VALUE1 : { STATEMENTS1
break;
}
case VALUE2 : { STATEMENTS2
break;
}
...
case VALUEn : { STATEMENTSn
break;
}
default : { STATEMENTSn+1 }
}
where EXPRESSION must compute to a value that is an integer
or a character. (Recall that Java characters are saved in storage as
integer.)
Each of VALUE1, VALUE2, ...,
must be integer or character literals (e.g., 2 or 'a'),
and no two cases can be labelled by the same constant value.
The semantics of the above variant of switch goes as follows:
A switch statement is often used to decode an input value that is a character. Imagine that an application reads Celsius ('C'), Fahrenheit ('F'), Kelvin ('K'), and Rankine ('R') temperatures---it likely reads a character code, call it letter, that denotes the temperature scale, and it is probably simplest to process the character with a statement of the form,
switch ( letter )
{ case 'C': { ...
break;
}
case 'F': { ...
break;
}
case 'K': { ...
break;
}
case 'R': { ...
break;
}
default: { System.out.println("TempConverter error: bad code"); }
}
to process the possible temperature scales.
Unfortunately, Java's switch statement has a primitive semantics that behaves badly when a break statement is omitted---more than one case might be executed! For this statement,
switch ( i )
{ case 2: { System.out.println("2");
}
case 5: { System.out.println("5");
j = j + i;
break;
}
default: { System.out.println("no"); }
}
when i holds 2, the control flow executes the statement,
System.out.println("2"),
and because of the missing break, control ``falls into''
the next case and executes
System.out.println("5") and j = j + i as well!
The break that follows sends the control to the end of the
switch.
An alternative to the switch statement is the following reformatted nested conditional, where certain bracket pairs are carefully omitted and indentation is made to look like that of the switch:
if ( i == 2 )
{ System.out.println("2"); }
else if ( i == 5 )
{ System.out.println("5");
j = j + i;
}
else if ( i == 7 )
{ System.out.println("7");
j = j - i;
}
else { System.out.println("none"); }
The Java compiler will read the above nested conditional the same
way as the one at the beginning of the Section.
Virtually all the applications constructed so far in this text used a simple architecture, the one seen in Figure 1, Chapter 4, where a controller asks an input-view for data, computes answers from the data, and sends those answers to an output-view. It is time to work with a more sophisticated architecture, of the form presented in Figure 9.
FIGURE 9: a simple model-view-controller architecture======================ENDFIGURE==============================================================
The controller decides the control flow of the application, the view(s) deal exclusively with input and output transmission, and the new component, the model, does the ``modelling'' of the problem and the ``computing'' of its answer. (In the Figure, the arrows suggest that the the controller sends messages to the input-view, asking for data; the controller then instructs the model to compute upon the data; and the controller next awakens the output-view and tells it to display the answers. Sometimes the model and output-view communicate directly---this is why the Figure also contains an arc between output-view and model. Also, it is common for the input and output views to be combined into one component, which we do ourselves in Chapter 10.)
We call the structure in Figure 3 a model-view-controller architecture.
(Footnote: The architecture in Figure 3 is a simplication of the model-view-controller architecture used in Smalltalk applications; the differences are discussed in Chapter 10. End Footnote.)
Why should we bother to build a program in so many pieces? There are three main answers:
In the ideal situation, the building of an application should be a matter of
As noted earlier, a model has the responsibility for ``modelling'' and ``computing'' the problem to be solved. This modelling is done with the methods and the field variables declared within the model class. (We call the field variables the model's attributes or its internal state.)
For example, a bank-account manager program uses a model that models an account ledger---the model has field variables to remember the account's balance, and the model owns methods for depositing and withdrawing funds, computing interest, and displaying the balance. A model for a chess game uses fields to model the playing board and pieces, and the model possesses methods that move pieces and compute interactions of pieces (e.g., ``captures''). And, a model of a weather prediction program models planet Earth by using field variables for land masses, air and water currents, and by using methods that compute the interaction of the fields.
A model is somewhat like the ``chip'' or ``board'' from a hand-held calculator (or other electronic appliance), because the model contains internal state, it contains operations that use the state, but it does not contain the calculator's input buttons or display panel (the ``views'') or the calculator's wiring and switches that instruct the chip what to do (the ``controller'').
In contrast, an application's controller takes responsibility for controlling the order in which the computation proceeds. The controller uses the input data to determine the appropriate control flow and to invoke the appropriate methods of the model to produce the output to be displayed. We use the techniques learned in the first part of the Chapter to write the controllers that appear in the sections to follow.
To design and build an application, we should follow these five steps:
First, we ask the program's user what the program is supposed to do; specifically, we ask the user how the program should behave in all of the cases when the user pushes a button, types some input data, and so on. (For example, if we are programming a text-editing program, we would ask the user to describe all the desired behaviors of the program --- entering text, pressing the ``Save File'' button, pressing the ``Undo'' button, and so on. For each behavior, we would list the program's response.)
Each activity is called a use-case behavior, or use case, for short. The collection of use cases helps us design the program's user interface (the view) so that all the desired buttons, text fields, dialogs, and displays are present. The use cases also help us design the program's model so that the model's class has methods to do all the desired computations.
If the application has a rich collection of use cases (e.g., a text-editing program), then a model-view-controller architecture is an appropriate choice; if there are only a few use cases, showing that the program's of computations are limited to just one or two forms (e.g., a Celsius-to-Fahrenheit convertor), then a simpler architecture, say, one that uses only a controller and a view, might be used. Extremely simple use cases warrant a one-component architecture.
The case study in Chapter 5 showed us how to write a specification for a class. We use this specification technique to design the classes for an application's model, whose methods are responsible for doing computations. Similarly, we design one or more classes for the view, which displays the results. (See again the case study in Chapter 5, which specified an output-view class.) Finally, we specify the controller component's main method and describe how the controller activates the methods in model and the view.
From each specification of each class, we write the Java coding of the class's attributes and methods. We test the classes one at a time; we can do this by writing small main methods that invoke the methods within the class. (The section, ``Testing Methods and Classes,'' presented later in this chapter, presents the details.) Or, if when using an IDE, we can type method invocations to the IDE, which sends them to the class and lets us see the results.
Finally, we assemble the classes into a complete program and test the program to see if it performs the actions specified in the original set of use-case behaviors.
We now consider a case study that employs the methodology.
A bank-accounts manager is a program that helps a user track her bank account balance --- the user enters the deposits and withdrawals, and the program maintains and displays a running balance. Say that we must design and build such an application, following the methodology just described. To better understand what the program must do, we begin by collecting use-case behaviors.
After some discussions with the potential users of the bank-account manager, perhaps we determine that the program's input is a sequence of commands, each of which must be one of the following forms:
Here is a sample use case: a user submits a deposit of $50.50 into an input dialog as follows:
(The d denotes ``deposit,'' of course.) The program responds to the deposit command by displaying the transaction and the current balance in the output view. The deposit of $50.50 would display
A second use case might illustrate a withdrawal of $30.33. Again, a command, say, D 30.33, would be typed into an input dialog, and the program's output view would show this:
Other use cases, illustrating both proper and improper behavior, should be considered:
The use cases also indicate that an output-view component must display the window that shows the account's balance. Finally, a controller is needed to generate input dialogs, send messages to the model to update the account, and send messages to the output view to display the results. This gives us the standard model-view-controller architecture, like the one displayed in Figure 9.
The model of the bank account must be specified by a class that remembers the the bank account's balance and owns methods for depositing and withdrawing money. The account's balance will be remembered by a field variable --- an attribute.
Table 10 presents the specification for class BankAccount, the model. We see the attribute and the two methods. Note also that
TABLE 10: specification of class BankAccount===================
| BankAccount models a single bank account | |
| Constructor method: | |
| BankAccount(int initial_balance) | initializes the bank account with initial_balance |
| Attribute | |
| private int balance | the account's balance, in cents; should always be a nonnegative value |
| Methods | |
| deposit(int amount): boolean | add amount, a nonnegative integer, to the account's balance. If successful, return true, if unsuccessful, leave balance alone and return false |
| withdraw(int amount): boolean | attempt to withdraw amount, a nonnegative integer, from the balance. If successful, return true, if unsuccessful, leave balance alone and return false |
ENDTABLE===========================================================The model's attribute, balance, remembers the account's balance. The attribute is an int variable, holding the balance, expressed in cents, in the account (e.g., 10 dollars is saved as 1000 cents); this eliminate troubles with fractions that arise when one maintains money with a double value.
Since balance is a private variable, it cannot be used directly by the client objects that use BankAccounts. Indeed, methods deposit and withdraw must be used to alter balance's value. Methods that alter the values of attributes are called mutator methods. Again, the specifications of deposit and withdraw are suffixed by a colon and boolean, which asserts that the methods return a boolean-typed result.
The algorithms for each of the model's methods are straightforward. For example, the one for deposit(int amount): boolean goes
The class based on the specification appears in Figure 11.
FIGURE 11: model class for bank account===================================
import javax.swing.*;
/** BankAccount manages a single bank account */
public class BankAccount
{ private int balance; // the account's balance
// representation invariant: balance >= 0 always!
/** Constructor BankAccount initializes the account
* @param initial_amount - the starting account balance, a nonnegative. */
public BankAccount(int initial_amount)
{ if ( initial_amount >= 0 )
{ balance = initial_amount; }
else { balance = 0; }
}
/** deposit adds money to the account.
* @param amount - the amount of money to be added, a nonnegative int
* @return true, if the deposit was successful; false, otherwise */
public boolean deposit(int amount)
{ boolean result = false;
if ( amount >= 0 )
{ balance = balance + amount;
result = true;
}
else { JOptionPane.showMessageDialog(null,
"BankAcccount error: bad deposit amount---ignored");
}
return result;
}
...
ENDFIGURE===============================================================
FIGURECONT 11: model class for bank account (concl.)================
/* withdraw removes money from the account, if it is possible.
* @param amount - the amount of money to be withdrawn, a nonnegative int
* @return true, if the withdrawal was successful; false, otherwise */
public boolean withdraw(int amount)
{ boolean result = false;
if ( amount < 0 )
{ JOptionPane.showMessageDialog(null,
"BankAcccount error: bad withdrawal amount---ignored"); }
else if ( amount > balance )
{ JOptionPane.showMessageDialog(null,
"BankAcccount error: withdrawal amount exceeds balance");
}
else { balance = balance - amount;
result = true;
}
return result;
}
/* getBalance reports the current account balance
* @return the balance */
public int getBalance()
{ return balance; }
}
ENDFIGURE===============================================================
Because attribute balance
is labelled private,
deposits and withdrawals are
handled by methods deposit and withdraw---this
prevents another malicious object from ``stealing money''
from the account!
The comment attached to balance states the representation
invariant that the field's value should always be nonnegative;
the representation invariant is a ``pledge'' that all methods (especially
the constructor method and withdraw) must preserve.
In addition to the methods listed in Table 10, the class contains an extra method, getBalance, which returns the account's balance. When an attribute, like balance, is listed in a specfication, it is a hint that a public method, like getBalance, will be included in the class to report the attribute's current value. A method that does nothing more than report the value of an attribute is called an accessor method.
The model class has the behaviors needed to maintain a bank account, but it does not know the order in which deposits and writhdrawals will be made---determining this is the responsibility of the controller part of the application.
Now that the model is written, we should test it. As hinted in the previous paragraph, we test the model by constructing an object from it and sending a sequence of method invocations to the object. The method invocations should mimick to some degree the possible use cases that motivated the application's design.
One simple, direct way to test the model is to write a main method that includes a sequence of method invocations. Here is one sample:
public static void main(String[] args)
{ BankAccount tester = new BankAccount(0); // construct a test object
// now, try the getBalance method:
System.out.println("Initial balance = " + tester.getBalance());
// try a deposit:
boolean test1 = tester.deposit(5050); // we deposit 5050 cents
System.out.println("Deposit is " + test1 + ": " + tester.getBalance());
// try a withdrawal:
boolean test2 = tester.withdraw(3033);
System.out.println("Withdrawal is " + test2 + ": " + tester.getBalance());
// try a mistake:
boolean test3 = tester.withdraw(6000);
System.out.println("Withdrawal is " + test3 + ": " + tester.getBalance());
// continue in this fashion....
}
The main method can be inserted into class BankAccount
and started from that class, or it can be placed into a small
controller class of its own.
As noted earlier, your IDE probably lets you construct the BankAccount object directly by selecting a menu item, and you can likely test the new object's methods by selecting another IDE menu item and entering the method invocations one at a time, e.g.,
tester.getBalance();and then
test.deposit(5050);and so on.
Table 12 lists the interface specifications for the input and output components. We use an output view to build the window that displays the account's balance, and for the first time, we write an input-view class whose responsibility is to disassemble input commands, like
D 50.50into their parts: a text string, "D", and an integer, 5050.
TABLE 12: specification for view components============================
| BankReader reads bank transactions from the user | |
| Methods: | |
| readCommand(String message): char | reads a new command line, prompting the user with message. It returns the first character of the user's response. |
| readAmount(): int | returns the integer value included in the most recently read input line |
| BankWriter writes transactions for a bank account | |
| Constructor method: | |
| BankWriter(String title, BankAccount b) | initializes the writer, where title is inserted in the window's title bar, and b is the bank account whose transactions is displayed |
| Methods: | |
| showTransaction(String message, int amount) | displays the result of a monetary bank transation, where message lists the transaction and amount is the numerical amount |
| showTransaction(String message) | displays the result of a monetary bank transation, where message lists the transaction. |
ENDTABLE============================================================Because BankWriter's constructor method takes no arguments, we omit it from the table.
Within BankWriter are two methods, both named showTransaction---we say that the method name is overloaded. Notice that the header lines of the two same-named methods have different forms of formal parameters: The first of the two methods is invoked when a showTransaction message with a string parameter and an integer parameter is sent to the BankWriter object; the second method is used when a showTransaction message is sent with just a string parameter.
Once the specifications of the various components are written, it is standard to insert the class, method, and attribute names from the specifications into the architectural diagram. Figure 13 shows this for the bank-account manager.
FIGURE 13: bank-account manager==========================================This picture is called a class diagram, because it diagrams the classes and how they are connected.ENDFIGURE============================================================
The model and view classes have already been developed; the AccountController uses a processTransactions method to control the flow of execution of the methods in the view and model components. Finally, we use a separate start-up class, AccountManager, to construct and connect the application's components.
Figure 13 displays a rich collaboration between the application's components. A collaboration between components is sometimes called a coupling; for example, the BankWriter is ``coupled'' to the BankAccount, which means the former cannot operate without the latter. Also, changes to BankAccount might affect the operation of BankWriter.
It is best not to have one component to which many others are coupled---if such a component's methods are changed, then many other components must be changed as well. In the Figure, we see that the model, BankAccount, is the most sensitive component in this regard. Also, since the controller is coupled to the most components, it is the most likely to be rewritten if there are changes to any part of the application.
An ideal software architecture will minimize the coupling between components so that changes in one component do not trigger revisions of many other components.
String input = " some data "; input = input.trim();This in effect removes the leading and trailing blanks from input, leaving the variable with the value "some data". The trim method is useful because users often carelessly add leading and trailing spaces to the input text they type, and the spaces sometimes interfere when checking for equality of strings, e.g,
if ( input.equals("some data") )
{ ... }
input = input.toUpperCase();assigns to input the string it formerly held, but converted to all upper-case letters. (Numerals, punctuation, and other symbols are left unchanged.)
There is also the method, toLowerCase, which operates similarly: S.toLowerCase() returns a string that looks like S except that all letters are translated to lower case.
char letter = input.charAt(0);extracts the leading character from the string, input. (Recall that the characters in a string are indexed 0, 1, 2, etc.) As noted in Chapter 3, characters can be saved in variables declared with data type char, such as the variable letter seen above.
Recall from Chapter 3 that a literal character is written with single quotes surrounding it, e.g., 'a', or 'F', or '4'. Characters can be compared with the comparison operations on integers, e.g., 'a' == 'A' computes to false.
The character in variable, letter, can be examined to see if it is, say, 'F', by the if-statement,
if ( letter == 'F' )
{ ... }
For example,
String first_two = input.substring(0, 3);assigns to first_two a string consisting of the first two characters from string input. Another example is
String remainder = input.substring(1, input.length());which assigns to remainder a string that looks like input less its leading character. (Recall that length() returns the number of characters in a string.)
Figure 14 displays the input-view class matching the specification.
FIGURE 14: input-view class for bank account manager======================
import javax.swing.*;
/** BankReader reads bank transactions from the user */
public class BankReader
{ private String input_line; // holds the most recent input command line
/** Constructor BankReader initializes the input reader */
public BankReader()
{ input_line = ""; }
/** readCommand reads a new command line
* @param message - the prompt to the user
* @return the first character of the command */
public char readCommand(String message)
{ // read the input line, trim blanks and convert to upper case:
input_line = JOptionPane.showInputDialog(message).trim().toUpperCase();
return input_line.charAt(0); // return the leading character
}
/** readAmount returns the numerical value included in the input command line
* @return the amount, converted entirely into cents; if there is
* no amount to return, announce an error and return 0. */
public int readAmount()
{ int answer = 0;
// extract substring of input_line that forgets the initial character:
String s = input_line.substring(1, input_line.length());
s = s.trim(); // trim leading blanks from substring
if ( s.length() > 0 ) // is there a number to return?
{ double dollars_cents = new Double(s).doubleValue();
answer = (int)(dollars_cents * 100); // convert to all cents
}
else { JOptionPane.showMessageDialog(null,
"BankReader error: no number for transaction---zero used");
}
return answer;
}
}
ENDFIGURE=================================================================
The BankReader uses readCommand to receive a new input command and return its character code (e.g., "D" for ``deposit''); a second method, readAmount, extracts the numerical amount embedded in the command. Of course, the initial character code is not part of the numerical amount, so the statement,
String amount = input_line.substring(1, input_line.length());uses the substring method to extract from input_line that subpart of it that starts at character 1 and extends to the end of the string. The statement,
answer = (int)(dollars_cents * 100);makes the fractional number, dollars_cents, truncate to an integer cents amount by using the cast, (int), into an integer. Finally, if the input line contains no number to return, the method returns zero as its answer, since bank transactions involving zero amounts are harmless.
Next, Figure 15 presents the output-view class. The constructor for class BankWriter gets the address of the BankAccount object for which the BankWriter displays information. (Remember from Chapter 5 that the address of an object can be a parameter to a method.) The BankAccount's address is used in the paint method, at bank.getBalance(), to fetch the account's current balance.
A private method, unconvert, reformats the bank account's integer value into dollars-and-cents format. The method uses the helper object, new DecimalFormat("0.00"), where the string, "0.00", states the amount should be formatted as a dollars-cents amount.
Also within BankWriter are the two methods both named showTransaction. The first of the two methods is invoked when a showTransaction message with a string parameter and an integer parameter is sent to the BankWriter object; the second method is used when a showTransaction message is sent with just a string parameter.
Overloading a method name is a cute ``trick'' and is sometimes used to great advantage (indeed, the method name, println, of System.out is overloaded), but it can be confusing as well. We take a closer look at overloading in Chapter 9.
FIGURE 15: output-view class for bank-account manager====================
import java.awt.*;
import javax.swing.*;
import java.text.*;
/** BankWriter writes bank transactions */
public class BankWriter extends JPanel
{ private int WIDTH = 300; // width and depth of displayed window
private int DEPTH = 200;
private BankAccount bank; // the address of the bank account displayed
private String last_transaction = ""; // the transaction that is displayed
/** Constructor BankAccount initializes the writer
* @param title - the title bar's text
* @param b - the (address of) the bank account displayed by the Writer */
public BankWriter(String title, BankAccount b)
{ bank = b;
JFrame my_frame = new JFrame();
my_frame.getContentPane().add(this);
my_frame.setTitle(title);
my_frame.setSize(WIDTH, DEPTH);
my_frame.setVisible(true);
}
public void paintComponent(Graphics g)
{ g.setColor(Color.white);
g.fillRect(0, 0, WIDTH, DEPTH); // paint the background
g.setColor(Color.black);
int text_margin = 50;
int text_baseline = 50;
g.drawString(last_transaction, text_margin, text_baseline);
g.drawString("Current balance = $" + unconvert(bank.getBalance()),
text_margin, text_baseline + 20);
}
/** unconvert reformats a cents amount into a dollars,cents string */
private String unconvert(int i)
{ double dollars_cents = i / 100.00;
return new DecimalFormat("0.00").format(dollars_cents);
}
...
ENDFIGURE========================================================
FIGURECONT 15: output-view class for bank-account manager (concl.)=====
/** showTransaction displays the result of a monetary bank transation
* @param message - the transaction
* @param amount - the amount of the transaction */
public void showTransaction(String message, int amount)
{ last_transaction = message + " " + unconvert(amount);
this.repaint();
}
/** showTransaction displays the result of a bank transation
* @param message - the transaction */
public void showTransaction(String message)
{ last_transaction = message;
this.repaint();
}
}
ENDFIGURE==============================================================
We can test the two new classes in the same way that we tested the model, class BankAccount: By using an IDE or writing a main method, we construct example input- and output-view objects from the two classes, and we send messages that invoke all the objects' methods with proper and improper arguments.
The last piece of the puzzle is the controller, AccountController, which fetches the user's transactions, dispatches them to the model for computation, and directs the results to the output view. The controller's algorithm for processing one transaction goes as follows:
account = new BankAccount(0);
writer = new BankWriter("BankWriter", account);
if ( TEST1 )
{ S1 }
else if ( TEST2 )
{ S2 }
else if ( TEST3 )
{ S3 }
else ...
The brackets around the else-arms are absent; this
is allowed when there is only one
statement in a conditional statement's
else-arm (in this case, it is another conditional).
The above format is an abbreviation for this heavily indented and
bracketed construction:
if ( TEST1 )
{ S1 }
else { if ( TEST2 )
{ S2 }
else { if ( TEST3 )
{ S3 }
else ...
}
}
As a rule, omitting an else-arm's brackets
is dangerous, and you should do so only when writing a
sequence of nested ifs in the above format.
FIGURE 16: controller for bank account manager===========================
/** AccountController maintains the balance on a bank account. */
public class AccountController
{ // fields that remember the view and model objects:
private BankReader reader; // input-view
private BankWriter writer; // output-view
private BankAccount account; // model
/** Constructor AccountController builds the controller
* @param r - the input-view object
* @param w - the output-view object
* @param a - the model object */
public AccountController(BankReader r, BankWriter w, BankAccount a)
{ reader = r;
account = a;
writer = w;
}
/** processTransactions processes user commands until a Q is entered */
public void processTransactions()
{ char command = reader.readCommand("Command (D,W,Q) and amount:");
if ( command == 'Q' ) // quit?
{ } // terminate method by doing nothing more
else { if ( command == 'D' ) // deposit?
{ int amount = reader.readAmount();
boolean ok = account.deposit(amount);
if ( ok )
{ writer.showTransaction("Deposit of $", amount); }
else { writer.showTransaction("Deposit invalid ", amount); }
}
else if ( command == 'W' ) // withdraw?
{ int amount = reader.readAmount();
boolean ok = account.withdraw(amount);
if ( ok )
{ writer.showTransaction("Withdrawal of $", amount); }
else { writer.showTransaction("Withdrawal invalid ", amount); }
}
else { writer.showTransaction("Illegal command: " + command); }
this.processTransactions(); // send message to self to repeat
}
}
}
ENDFIGURE==========================================================
FIGURECONT 16: controller for bank account manager (concl.)=========
/** AccountManager starts the application that maintains a bank account. */
* Inputs: a series of commands of the forms,
* D dd.cc (deposit),
* W dd.cc (withdraw), or
* Q (quit), where dd.cc is a dollars-cents amount
* Outputs: a display of the results of the transactions */
public class AccountManager
{ public static void main(String[] args)
{ // create the application's objects:
BankReader reader = new BankReader();
BankAccount account = new BankAccount(0);
BankWriter writer = new BankWriter("BankWriter", account);
AccountController controller =
new AccountController(reader, writer, account);
// start the controller:
controller.processTransactions();
}
}
ENDFIGURE===============================================================
Testing the controller must be done a bit differently that testing the other components, because the controller relies on other classes to do much of the work. When we examine Figure 5, we see that the controller depends on BankReader, BankWriter, and BankAccount. How do we test the controller? There are two approaches:
public class BankAccount
{ // there are no attributes
public BankAccount(int initial_amount) { } // does nothing
public boolean deposit(int amount)
{ System.out.println("deposit of " + amount);
return true; // the method must return some form of result
}
public boolean withdraw(int amount)
{ System.out.println("withdrawal of " + amount);
return true;
}
public int getBalance()
{ return 0; }
}
The dummy class contains only enough instructions so that the Java
compiler can process it and the controller can construct a dummy
object and send messages to it.
A typical dummy class is little more that the class's specification
plus a few println and return statements.
This makes it easy to write dummy classes quickly and do tests on just
of the controller.
This approach can make controller testing more demanding, because errors might be due to problems in the controller's coding or due to problems in the interaction of the components. Often, a mixture of dummy classes and a completed classes, added one at a time, can ease this difficulty.
As stated earlier, integration testing should attempt, at least, all the use-case behaviors that motivated the design of the application.
/** depositInterest increases the account with an interest payment, * calculated as (interest_rate * current_balance) * @param rate - the interest rate, a value between 0.0 and 1.0 * @return the amount deposited into the account; if the deposit cannot * be performed, return 0 */ public int depositInterest(double rate)and add the input command, I dd.d, which allows the user to increase the account's current balance by dd.d%.
We finish the bank-account case study with a small but crucial modification: Since many people have multiple bank accounts, we modify the account-manager application to manage two distinct bank accounts simultaneously---a ``primary account'' and a ``secondary account.''
The architecture in Figure 12 stays the same, but we annotate its arcs with numbers to make clear that the one controller now collaborates with two models. As a consequence, each model is mated to its own output view, meaning there are two output views in the complete program. See Figure 17.
FIGURE 17: program architecture with two bank accounts==================ENDFIGURE===============================================================
In the Figure, read the numbering of the form
as stating, ``each 1 A-object is coupled to (uses or sends messages to) m B-objects.'' (An unannotated arrow is a 1-1 coupling.)
To build this architecture, we reuse all the classes we have and modify the controller. The new controller, AccountManager2, will process the same input commands as before plus these two new ones:
Command (P,S,D,W,Q):P Command (P,S,D,W,Q):d 50.50 Command (P,S,D,W,Q):s Command (P,S,D,W,Q):D10.00 Command (P,S,D,W,Q):p Command (P,S,D,W,Q):W 30.33 Command (P,S,D,W,Q):qJust before the user quits, the output views look like this:
The modified program uses two models, called primary_account and secondary_account; each model has its own output-view, primary_writer and secondary_writer, respectively.
It is crucial that the controller remember which of the two accounts is active and is the target of the transactions. For this purpose, the controller uses the fields private BankAccount account and private BankWriter writer to hold the addresses of the account and its view that are active. The fields are initialized to the (addresses of the) primary account objects.
Figure 18 presents the modified controller.
FIGURE 18: controller for managing two bank accounts=====================
/** AccountController2 maintains the balance on two bank accounts, a primary
* account and a secondary account.
* inputs: P (use primary account), S (use secondary account),
* D dd.cc (deposit), W dd.cc (withdraw), Q (quit)
* outputs: the transactions displayed on two windows */
public class AccountController2
{ private BankReader reader; // input view
// the primary bank-account: model and its output-view:
private BankAccount primary_account;
private BankWriter primary_writer;
// the secondary bank-account: model and its output-view:
private BankAccount secondary_account;
private BankWriter secondary_writer;
// fields that remember which model and view are active for transactions:
private BankAccount account;
private BankWriter writer;
// invariant: these fields must belong to the primary or secondary account
/** AccountController2 initializes the bank accounts */
public AccountController2(BankReader r, BankAccount a1, BankWriter w1,
BankAccount a2, BankWriter w2)
{ reader = r;
primary_account = a1;
primary_writer = w1;
secondary_account = a2;
secondary_writer = w2;
// start processing with the primary account:
account = primary_account;
writer = primary_writer;
}
/** resetAccount changes the current account to new_account and new_writer */
private void resetAccount(BankAccount new_account, BankWriter new_writer)
{ writer.showTransaction("Inactive"); // deactivate current account
account = new_account; // reset the account to the new one
writer = new_writer;
writer.showTransaction("Active");
}
...
ENDFIGURE===========================================================
FIGURECONT 18: controller for managing two bank accounts (concl.)=========
/** processTransactions receives user commands until a Q is entered */
public void processTransactions()
{ char command = reader.readCommand("Command (P,S, D,W,Q):");
if ( command == 'Q' ) // quit?
{ }
else { if ( command == 'D' ) // deposit?
{ int amount = reader.readAmount();
account.deposit(amount);
writer.showTransaction("Deposit of $", amount);
}
else if ( command == 'W' ) // withdraw?
{ int amount = reader.readAmount();
boolean ok = account.withdraw(amount);
if ( ok )
{ writer.showTransaction("Withdrawal of $", amount); }
else { writer.showTransaction("Withdrawal invalid", amount); }
}
else if ( command == 'P' ) // work with primary account?
{ resetAccount(primary_account, primary_writer); }
else if ( command == 'S' ) // work with secondary account?
{ resetAccount(secondary_account, secondary_writer); }
else { writer.showTransaction("Illegal command"); }
this.processTransactions(); // send message to self to repeat
}
}
}
/** AccountManager2 maintains two bank accounts */
public class AccountManager2
{ public static void main(String[] args)
{ BankReader reader = new BankReader();
// create the models and their views:
BankAccount primary_account = new BankAccount(0);
BankWriter primary_writer
= new BankWriter("Primary Account", primary_account);
BankAccount secondary_account = new BankAccount(0);
BankWriter secondary_writer
= new BankWriter("Secondary Account", secondary_account);
// construct the controller and start it:
AccountController2 controller = new AccountController2(reader,
primary_account, primary_writer, secondary_account, secondary_writer);
controller. processTransactions();
}
}
ENDFIGURE===============================================================
Within processTransactions,
conditional statements are used to
detect the new commands, P and S, and adjust the values
in the account and writer fields accordingly.
When you start this application, you will see two graphics windows appear on the display---one for the primary account and one for the secondary account. (Perhaps the two windows will first appear on top of each other; use your mouse to move one of them. Or, you can use the setLocation method---f.setLocation(x ,y) positions the upper left corner of frame f at coordinates x, y on the display.)
When the program is started, it creates the following configuration in computer storage:
Two BankAccount and BankWriter objects appear, and the fields account and writer hold the addresses of the objects that the user manipulates with deposits and withdrawals. When the user selects the secondary account, the two fields receive the values a5 and a6, respectively.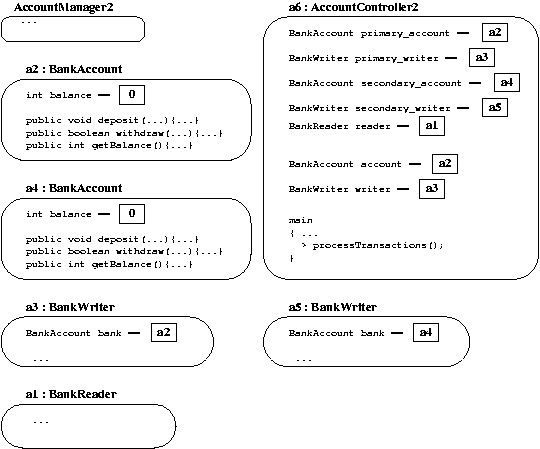
Class BankAccount has been used to generate multiple bank account objects, just as we might use a blueprint to build several houses. In the chapters that follow, we make good use of this principle to construct multiple objects that work in ensemble to solve significant problems.
As suggested by the earlier case study, to test a class, we must test its methods. When testing an individual method, think of the method as a ``little main method,'' whose input arguments arrive by means of actual parameters---we write lots of invocations of the methods with lots of different actual parameters. Therefore, the techniques we learned earlier for testing entire applications apply to testing individual methods: (Reread the section, ``Testing a Program that Uses Input,'' in Chapter 4, for details.)
Test a method with both ``white box'' and ``black box'' techniques that ensure that each statement in the method is executed in at least one test case.
In particular, when a method contains if-statements, be certain to formulate enough tests so that every arm of every if-statement is executed by at least one test. Although this strategy does not guarantee correctness of the entire method, it should be obvious that an error inside the arm of a conditional will never be detected if the arm is never executed! You might draw a flowchart of a method to help devise the test cases that ensure each possible control flow is tested at least once.
Unfortunately, we cannot always test each method of a class independently---if a class's method references a field variable (an attribute), then the value in the attribute affects how the method behaves. To complicate matters further, if the attribute is shared by multiple methods in the class, then the manner in which all the methods use the field becomes crucial to the correct behavior of each method.
We deal with this situation in two stages: The first is to consider how a single method interacts with a class's attrbutes; the second is to consider the order in which a family of methods use the attributes.
We consider the first stage now: Given one single method, we must identify the attributes used by the method. For each attribute, we list the range of values that the method would find acceptable as the attribute's value. Then, we initialize the attribute with sample values within this range and do multiple invocations of the method to observe the interactions between the method and the attribute. At the same time, whenever the method changes the value of an attribute, we check that the new value assigned to the attribute is acceptable.
For example, we might test the withdraw method of class BankAccount from Figure 11. The method uses the class's balance attribute, so we consider the acceptable range of values for that attrbute, and decide that balance should always hold a nonnegative integer. So, we might test the withdraw method by initializing balance to a nonnegative as follows:
public class BankAccount
{ private int balance = 44; // pick some value for initialization
// We are not yet testing the constructor method, so leave it empty:
public BankAccount() { }
public boolean withdraw(int amount)
{ boolean result = false;
if ( amount < 0 )
{ ... }
else ...
return result;
}
}
Now we are ready for a round of test invocations of withdraw with
a variety of arguments. After each invocation, we check the
value of balance and verify that withdraw assigned
an acceptable value.
As we systematically test a class's methods one by one, we will reach a consensus regarding the attribute's range of values that is acceptable to all the class's methods. This helps us establish the representation invariant for each attribute and eases the second stage of method testing.
Because methods typically share usage of a class's attributes, the order in which a class's methods are invoked can affect the behavior of the methods themselves. For example, it is potentially a problem if a new BankAccount object is constructed with an initial balance of zero, and we invoke the withdraw method before doing any deposits!
A more subtle problem arises when several methods share an attribute, and one method inserts an unacceptable value into the attribute; this negatively impacts the other methods, which assume that the attribute always holds acceptable values.
We might tackle this situation by generating
test cases that include
all possible sequences of method invocations, but this is daunting.
A better solution is to rely on the
representation invariants that we formulated based on the
testing of the
individual methods:
Recall that a representation invariant is a property about a field that must always be preserved, no matter what updates are made to the field. Such an invariant typically states some ``reasonable range of values'' that a field may have. If all of a class's methods pledge to preserve the representation invariant, then each method can be tested individually, where, as part of the testing, the representation invariant is verified as preserved by the method.
For example, in class BankAccount the representation invariant for balance states that balance's value is always nonnegative; each method promises to preserve this invariant. To test the deposit method, we first set balance to a nonnegative value, so that the representation invariant is true. Then, we test deposit with an actual parameter. After the test, we verify that deposit behaved properly and that balance retains a nonnegative value. Similarly, the withdraw method and the class's constructor method must be tested to verify that they preserve balance's representation invariant.
In this way, we alter our approach to testing a suite of methods---we do not worry about the order in which the methods are invoked; instead, we validate that, regardless of the order in which a class's methods are invoked, all attributes' values are safely maintained to be acceptable to the representation invariants.
When one method is invoked, it might invoke other methods. In this situation, you might require extra assistance in understanding exactly what one method does in terms of other methods; a good way of obtaining this understanding is by generating a mechanical execution trace during a test invocation of a method.
In this text, we have seen handwritten execution traces from time to time. Indeed, the best way to learn about execution patterns of an invoked method is to write an execution trace by hand! But if you lack pencil and paper, it is possible to make method generate its own execution trace by this simple trick: insert println statements into its body and the bodies of the methods it invokes---have each method print, at entry to its body, the values of its parameters and the field variables it uses. When the method's body finishes, it prints the values of fields and important local variables.
Of course, if you are using an IDE you can use the IDE's ``debugger'' to generate execution traces, and you do not have to insert the println statements. Instead, you tell the debugger to insert ``breakpoint'' lines at the statements where you wish to see the values of parameters and fields. Then, you start the program, and the debugger lets the program execute until a breakpoint line is encountered. At the breakpoint line, the debugger pauses the program, and you can ask the debugger to print variables' values. Once you have seen all the values you desire, you tell the debugger to resume execution.
Using the println technique, we can alter deposit to generate its own execution trace as follows:
public void deposit(int amount)
{ System.out.println("deposit ENTRY: amount = " + amount
+ " balance = " + balance);
balance = balance + amount;
System.out.println("deposit EXIT: balance = " + balance);
}
The trace information proves especially useful to understanding
the order in which methods are
invoked and the values the methods receive and return.
When one method invokes another, we can adapt the ``dummy class'' (``stub'') technique so that we can test one method even if the methods invoked are not yet coded---we write ``dummy'' methods for the methods not yet coded. (The dummy methods must respect the representation invariants, of course.) For example, if we have written deposit but not the other methods of BankAccount, we might build the following class for testing:
public class BankAccount
{ private int balance; // representation invariant: balance >= 0
public BankAccount(int initial_balance)
{ balance = 0; } // dummy --- this assignment makes the invariant true
public void deposit(int amount)
{ balance = balance + amount; }
public boolean withdraw(int amount)
{ return true; } // dummy
public int getBalance() { return 0; } // dummy
}
The bodies of the yet-to-be-coded methods, BankAccount,
withdraw, and getBalance, are represented by harmless,
dummy methods that preserve balance's representation invariant.
if ( hours >= 0 )
{ JOptionPane.showMessageDialog(null,
hours + " hours is " + seconds + " seconds");
}
else { JOptionPane.showMessageDialog(null,
"ConvertHours error: negative input " + hours);
}
if ( (dollars < 0) || (cents < 0) || (cents > 99) )
{ ... }
if ( hours < 0 )
{ String error = "convertHoursIntoSeconds error: bad hours " + hours;
JOptionPane.showMessageDialog(null, error);
throw new RuntimeException(error);
}
switch ( letter )
{ case 'C': { ...
break;
}
case 'F': { ...
break;
}
case 'K': { ...
break;
}
case 'R': { ...
break;
}
default: { System.out.println("TempConverter error: bad code"); }
}
/** showTransaction displays the result of a monetary bank transation
* @param message - the transaction
* @param amount - the amount of the transaction */
public void showTransaction(String message, int amount)
{ last_transaction = message + " " + unconvert(amount);
repaint();
}
/** showTransaction displays the result of a bank transation
* @param message - the transaction */
public void showTransaction(String message)
{ last_transaction = message;
repaint();
}
if ( hour >= 13 )
{ answer = answer + (hour - 12); }
else { if ( hour == 0 ) ... }
as seen above; the test is hour >= 13).
The possible control flows are the conditional's then-arm
(e.g., answer = answer + (hour - 12)) and
the else-arm (e.g., if ( hour == 0 ) ...).
When the test results in
true, the then-arm is executed; when the test results in
false, the else-arm is executed.
if ( TEST )
{ // here, assume TEST is true
STATEMENTS1 // use the assumption to reach some goal, G
}
else { // here, assume !TEST is true
STATEMENTS2 // use the assumption to reach some goal, G
}
// regardless of outcome of TEST, goal G is achieved
Another temperature scale is Kelvin, which is defined in terms of Celsius as follows:
K = C + 273.15(For example, 10 degrees Celsius is 283.15 degrees Kelvin.)
Write a class TempCalculator with these methods:
| celsiusIntoFahrenheit(double c): double | translate the Celsius temperature, c, into its Fahrenheit value and return it as a double |
| fahrenheitIntoCelsius(double f): double | translate the Fahrenheit temperature, f, into its Celsius value and return it as a double |
| celsiusIntoKelvin(double c): double | translate the Celsius temperature, c, into its Kelvin value and return it as a double |
| kelvinIntoCelsius(double k): double | translate the Kelvin temperature, k, into its Celsius value and return it as a double |
| fahrenheitIntoKelvin(double f): double | translate the Fahrenheit temperature, c, into its Kelvin value and return it as a double |
| kelvinIntoFahrenheit(double k): double | translate the Kelvin temperature, k, into its Fahrenheit value and return it as a double |
| Constructor | |
| Money(int initial_amount) | Construct a new object such that it holds initial_amount of money. |
| Attribute | |
| private int amount | the amount of money not yet converted into change |
| Method | |
| extract(int coins_value): int | extract the maximum quantity possible of the coin with the value, coins_value, from the amount of money. Reduce the value of amount accordingly, and return as the answer the number of coins that were extracted. |
| Constructor | |
| Mortgage(double p, double i, int y) | Construct a new object based on the starting principal, p, the loan's interest rate, i, and the number of years, y, needed to repay the loan. (Note: interest, i, is expressed as a fraction, e.g., 10% is 0.10.) |
| Attributes | |
| private double monthly_payment | the loan's monthly payment, as calculated from the starting principal, interest rate, and duration. (See the formula following this Table.) |
| private double remaining_principal | how much is left to repay of the loan |
| private double total_paid | the total amount of monthly payments paid so far |
| Methods | |
| makeMonthlyPayment() | make one monthly payment towards the loan, increasing the total_paid and reducing the remaining_principal. (See the formula following the Table.) |
(1 + i)y *p*i
payment = -----------------
(1 + i)y - 1
monthlyPayment = payment / 12.0
for principal, p, interest rate, i, and years, y.
newPrincipal = ( (1+(i/12))remaining_principal ) - paymentwhere i and payment are as above.
Once you complete the model, use it in an application that lets a user submit a starting principal, interest rate, and loan duration. The application replies with the monthly payment. Then, each time the user presses the button on a dialog, the application makes a monthly payment and displays the remaining principal and the total paid so far. The user continues to press the dialog's button until the loan is paid in full.
distance = V0t + (1/2)a(t2)Use this formula to ``model'' a moving automobile: class Auto must have internal state that remembers (at least) the auto's initial velocity and acceleration, and it must have a method that returns the auto's current position (distance).
Once you complete the model, use it in an application that lets a user submit a starting velocity and acceleration. Then, each time the user presses the button on a dialog, the application adds one unit to the time and displays the distance travelled by the auto.
/\ / \ ----- | _ | |x| |x| -----Of course, the building must be drawn before the roof, and the roof must be drawn before the doors and windows.
In addition to the class that represents the die, write a model class that represents the state of a partially built house. Then, write an output view that displays the house, and write a controller that enforces the rules of the game.
Two of the methods might be
| insertMoney(int amount) | the customer inserts the amount of money into the vending machine, and the machine remembers this. |
| askForCoffee(): boolean | the customer requests a cup of coffee. If the customer has already inserted an adequate amount of money, and the machine still has coffee in it, the machine produces a cup of coffee, which it signifies by returning the answer, true. If the machine is unable to produce a cup of coffee, false is returned as the answer. |
Next, write an output-view of the vending machine and write an input-view and controller that help a user type commands to ``insert'' money and ``buy'' coffee and tea from the machine.
--------------------------- | __ | | / .\ | | ----- | | | | | | | | | | | ---------------------------The input commands to the program consist of F (move forwards one mouse-length), L (turn left), R (turn right). Write a model that remembers the position of the mouse in the box and the direction the mouse is pointed; the model will have methods that let the mouse move forwards and turn left and right. Then, write an output view that draws a picture of the mouse within the box. Finally, write a controller that transfers the commands to the model.
!(P || Q)yields the same results as that of
!P && !QIndeed, here are valuable logical equivalences that simplify relational expressions:
!(P || Q) is equivalent to !P && !Q !(P && Q) is equivalent to !P || !Q !!P is equivalent to P P && (Q && R) is equivalent to P && Q && R is equivalent to (P && Q) && R P || (Q || R) is equivalent to P || Q || R is equivalent to (P || Q) || RBy reading and employing these equivalences from left to right, you can minimize the occurrences of parentheses and negations in a logical expression. For example, the difficult-to-understand expression, !(x < 0 || (y <= 10 && y != 1)), simplifies as follows:
!(x < 0 || (y <= 10 && y != 1)) is equivalent to !(x < 0) && !(y <= 10 && y != 1) is equivalent to x >= 0 && (!(y <= 10) || !( y != 1)) is equivalent to x >= 0 && (y > 10 || y == 1)
Since we used relational operations to compress the structure of nested conditionals, we should not be surprised to learn that there is a connection between symbolic logic and the conditional statement. The connection can be stated as follows:
if ( TEST )
{ // here, assume TEST is true
STATEMENTS1 // use the assumption to reach some goal, G
}
else { // here, assume !TEST is true
STATEMENTS2 // use the assumption to reach some goal, G
}
// regardless of outcome of TEST, goal G is achieved
That is, the then-arm's statements
can assume the logical truth
of the test when the statements execute.
Similarly, the else-arm's statements can assume the falsity of the test.
Both arms should be dedicated to completing an overall, common goal.
For example, consider this simple method, whose goal is to compute the absolute value of an integer:
public int abs(int n)
{ int answer;
if ( n < 0 )
{ answer = -n; }
else { answer = n; }
return answer;
}
The goal of the conditional statement is to assign the absolute
value of n into answer. To validate that
the goal is achieved, we annotate the conditional and study its arms:
if ( n < 0 )
// assume n < 0:
{ answer = -n; }
// goal: answer holds |n|
else // assume !(n < 0), that is, n >= 0:
{ answer = n; }
// goal: answer holds |n|
The assumptions derived from the test help us deduce that both arms
achieve the goal.
Here is a more significant example: Consider the crucial step in Figure 7, where a 24-hour time is translated into a twelve-hour time---the calculation of the hours amount. The nested conditional that does this is extracted from Figure 7:
// assume !( hour < 0 || hour > 23 || minute < 0 || minute > 59 )
// that is, !(hour < 0) && !(hour > 23) && !(minute < 0) && !(minute > 59)
// that is, hour >= 0 && hour <= 23 && minute >= 0 && minute <= 59
if ( hour >= 13 )
{ answer = answer + (hour - 12); }
else { if ( hour == 0 )
{ answer = answer + "12"; }
else { answer = answer + hour; }
}
// goal: append correct hour to answer
Because this conditional statement is itself
is nested within the else-arm of the outermost
conditional,
we can assume that it executes only when the outer conditional's test
computes to false. Because of the logical equivalences stated above,
we uncover that the hours value falls in the range 0..23,
which is crucial to the computation that follows.
The overall goal of the nested conditional is to append to answer the correct twelve-hour representation of hours. We can verify the goal by considering the outcomes of the first test:
// assume hour >= 0 && hour <= 23 && minute >= 0 && minute <= 59
if ( hour >= 13 )
// assume that hour >= 13
// more precisely, assume hour >= 13 && hour >= 0 && hour <= 23
// that is, hour >= 13 && hour <= 23
{ answer = answer + (hour - 12); }
// goal: append correct hour to answer
else // assume that !(hour >= 13), that is, hour < 12
// more precisely, assume hour < 12 && hour >= 0 && hour <= 23
// that is, hour >= 0 && hour < 12
{ if ( hour == 0 )
{ answer = answer + "12"; }
else { answer = answer + hour; }
}
// goal: append correct hour to answer
The conditional's arms are commented with the outcomes of the test.
Most importantly, we may carry the assumption that held true at the
beginning of the conditional into its two arms and use it
to deduce precise information about the range of values hour
might possess.
Consider the then-arm:
// assume hour >= 13 && hour <= 23
{ answer = answer + (hour - 12); }
// goal: append correct hour to answer
The assumption tells us exactly what we must know to validate that
subtraction by 12 is the correct conversion to achieve the goal.
The else-arm can be analyzed similarly:
// assume hour >= 0 && hour < 12
{ if ( hour == 0 )
{ answer = answer + "12"; }
else { answer = answer + hour; }
}
// goal: append correct hour to answer
Our analysis of the else-arm's
test produces these additional assumptions:
if ( hour == 0 )
// assume hour == 0 && hour >= 0 && hour < 12
// that is, hour == 0
{ answer = answer + "12"; }
// goal: append correct hour to answer
else // assume !(hour == 0) && hour >= 0 && hour < 12
// that is, hour > 0 && hour < 12
{ answer = answer + hour; }
// goal: append correct hour to answer
Again, the logical assumptions help us validate that for both
control flows the goal is achieved. In summary, all cases
are validated, and the nested conditional achieves its goal.
Logical reasoning like that seen here is a powerful tool that helps a programmer understand control flow and validate correct behavior prior to testing. Indeed, logical reasoning helps one write a conditional statement correctly, because the test part of the conditional should ask exactly the precise question that gives one the logical information needed to validate that the conditional's arms achieve the overall goal.
public class Counter
{ private int count;
public Counter()
{ count = 0; }
public boolean increment()
{ count = count + 1;
return true;
}
public boolean equalsZero()
{ return (count == 0); }
}
Say that we have this situation:
Counter c = new Counter();
if ( TEST )
{ ... }
/** max returns the larger value of its three arguments
* @param x - the first argument
* @param y - the second argument
* @param z - the third argument
* @return the largest of the three */
public int max(int x, int y, int z)
{ int big;
if ( x >= y && x >= z )
{ big = x; }
else { if ( y >= z )
{ big = y; }
else { big = z; }
}
return big;
}
/** max returns the largest value of its three arguments.
* The parameters and returned result are the same as above. */
public int max(int x, int y, int z)
{ int big = x;
if ( y > big )
{ big = y; }
if ( z > big )
{ big = z; }
return big;
}
Testing classes one by one does not ensure that the completed application will behave as expected---sometimes the interaction between objects goes unexpectedly wrong. This is not supposed to happen, but the problem can arise when the designer of a method has not specified clearly (i) the conditions under which an object's method should be used and (ii) the form of result the method produces. A standard format, or interface specification, for methods is needed to help them integrate correctly. The interface specifications that we used in Tables 10 and 12 in this Chapter are good starting examples.
Unfortunately, the Java compiler does not force a programmer to write specifications like those in Tables 10 and 12. Indeed, the compiler merely requires that each method possess a header line that lists the data types of the method's parameters and the data type of the returned result, if any. The Java compiler uses the header line to ensure that every invocation of the method uses the correct quantity and data typings of actual parameters. The compiler also checks that the result returned from the method can be correctly inserted into the place of invocation.
But the compiler's checks are not enough. Say that a programmer has miscoded the deposit method from class BankAccount in Figure 11 as follows:
public void deposit(int amount)
{ balance = balance * amount; }
Although this coding violates the specification in Table 10,
the Java compiler does not notice the problem.
This is a disaster---other programmers, building other classes,
will rely on Table 10 as the correct specification
for class BankAccount,
meaning that the BankAccount objects they create and use are
faulty.
The point is a programmer is morally bound to build a class that correctly matches its interface specification. To remind the programmer of her obligation, in this text we require that each method be prefixed by comments taken from the class's specification. Also, once the class is completed, the javadoc program can be used to generated the Web page description for the class. (See the section, ``Generating Web Documentation with javadoc,'' in Chapter 5.)
A well-written interface specification will state concisely the nature of a method's parameters, what the method does, and what result, if any, the method produces. Let's examine the specfication for method withdraw from Figure 11:
/* withdraw removes money from the account, if it is possible. * @param amount - the amount of money to be withdrawn, a nonnegative int * @return true, if the withdrawal was successful; return false, if the * amount to be withdrawn was larger than the account's balance */ public boolean withdraw(int amount)Notice the remark attached to parameter amount: It states that the actual parameter must be a nonnegative int. This requirement of the parameter is called a precondition; the correct behavior of the method is guaranteed only when this condition holds true for the actual parameter. A precondition is like the statement of ``acceptable conditions of use'' that one finds in a warranty that comes with a household appliance. (A real-life example: ``This television is for indoor use only.'')
The @return comment, which describes the result value, is called the postcondition. The clients (users) of the method trust the postcondition to state the crucial property of the method's result. The clients use the postcondition to validate their own work. (For example, the validation of the controller, AccountManager, depends crucially on withdraw accomplishing what is promised in its postcondition.)
When a method has no @return clause (that is, its return type is void), then the first sentence of the comment, which describes the behavior of the method, acts as the postcondition. The specification for method deposit is a good example:
/** deposit adds money to the account. * @param amount - the amount of money to be added, a nonnegative int */ public void deposit(int amount)
Because an interface specification is a specification for object connection, it should state all key information for using the object's methods; a programmer should not be required to read the body of a method that someone else has written in order to invoke it---reading the method's specification should suffice. This requirement is essential for creating classes that others can use.
Programmers often call a class's interface specification its API (application programming interface).
If a large application is developed by a group of people, and if the people agree to use specifications like the ones in this Chapter, it becomes possible for each person to design, code, and test a part of the application independently of the other parts. (At the testing stage, one can write ``dummy classes'' to represent the unfinished classes that others are writing.)
The specifications used in this text are somewhat informal, but they are better than none at all. Indeed, this is why the designers of the Java language developed the javadoc documentation program---a programmer can generate useful APIs while writing her programs.
Indeed, since javadoc does not execute the class that it reads, it will generate API documentation for an incomplete class. For example, if a multi-class application must be written by a team of people, it is useful to have the API documentation for all classes available as soon as possible, even before the classes are completed. One can write the interface specifications, attach empty method bodies to them, and supply them to javadoc. Here is such a dummy class from which javadoc generates a useful API:
/** BankAccount manages a single bank account */
public class BankAccount
{
/** Constructor BankAccount initializes the account
* @param initial_amount - the starting account balance, a nonnegative. */
public BankAccount(int initial_amount)
{ }
/** deposit adds money to the account.
* @param amount - the amount of money to be added, a nonnegative int */
public void deposit(int amount)
{ }
/* withdraw removes money from the account, if it is possible.
* @param amount - the amount of money to be withdrawn, a nonnegative int
* @return true, if the withdrawal was successful; false, if the amount
* to be withdrawn was larger than the account's balance */
public boolean withdraw(int amount)
{ }
/* getBalance reports the current account balance
* @return the balance */
public int getBalance()
{ }
}
Finally, here is a warning about typing the Java commentary for an interface specfication: A method's commentary is enclosed within comment markers, /** and */. Don't forget the */! The following class compiles with no errors, yet it is missing one of its methods:
class M
{ /** f's description goes here.
* @param i - parameter info
* @return information
public int f(int i) { return i+1; }
/** comment for g goes here.
* @param x - parameter info */
public void g(String x) { System.out.println(x); }
}
The problem is the missing */ in the commentary for f.
Because of the missing comment marker, the code for f is
treated as a comment that merges into g's comments.
Hence, only g is compiled in class M.
You will notice the problem only later when you try to invoke
f from another program
and you receive a mysterious message from the compiler stating
that f does not exist.