


2.12.4 Multiple Independent Poisson ProcessesSuppose that there are two Poisson processes operating independently, with arrival rates 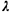 1 and 1 and 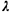 2 respectively. N1(t) and
N2(t) are the respective cumulative numbers of arrivals
through time t. Then the combined or pooled process has a cumulative number of arrivals equal to N(t) =
N1(t) + N2(t). A fundamental property of independent Poisson processes
is that their pooled process is also a Poisson process with
arrival-rate parameter equal to the sum of the individual arrival
rates. Thus, N(t) has a Poisson distribution with mean ( 2 respectively. N1(t) and
N2(t) are the respective cumulative numbers of arrivals
through time t. Then the combined or pooled process has a cumulative number of arrivals equal to N(t) =
N1(t) + N2(t). A fundamental property of independent Poisson processes
is that their pooled process is also a Poisson process with
arrival-rate parameter equal to the sum of the individual arrival
rates. Thus, N(t) has a Poisson distribution with mean (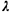 1 + 1 + 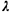 2)t. This result extends in the obvious way
to more than two independent Poisson processes. There are many ways to prove
this result, but the simplest is just to observe that the pooled
process satisfies each of the four postulates of the Poisson process. 2)t. This result extends in the obvious way
to more than two independent Poisson processes. There are many ways to prove
this result, but the simplest is just to observe that the pooled
process satisfies each of the four postulates of the Poisson process.We are often confronted with the following question: Given two independently operating Poisson processes with rate parameters 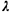 1 and 1 and 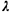 2 respectively, what is the probability that an arrival from process 1 (a "type 1" arrival) occurs before an arrival from process 2
(a "type 2" arrival)? To solve this problem, let the two arrival
times of interest be denoted by X1 and X2, for processes 1 and 2,
respectively. We want to compute P{X1 < X2}. Invoking our knowledge
of Poisson processes, we know that the pdf's for X1 and X2 are
negative exponentials with means 2 respectively, what is the probability that an arrival from process 1 (a "type 1" arrival) occurs before an arrival from process 2
(a "type 2" arrival)? To solve this problem, let the two arrival
times of interest be denoted by X1 and X2, for processes 1 and 2,
respectively. We want to compute P{X1 < X2}. Invoking our knowledge
of Poisson processes, we know that the pdf's for X1 and X2 are
negative exponentials with means 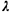 1-1 and 1-1 and 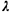 2-1, respectively. Thus, because of independence, the joint pdf is 2-1, respectively. Thus, because of independence, the joint pdf is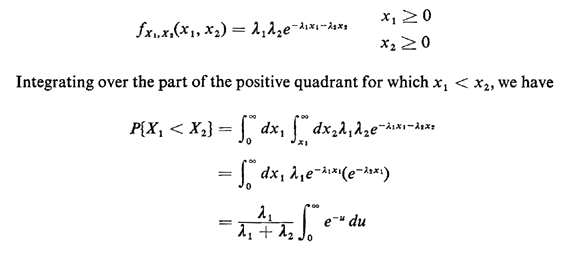
or, since the integral equals 1, 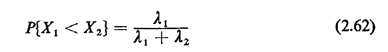
This result makes sense intuitively: The probability that a type 1 arrival occurs before a type 2 arrival is equal to the fraction of the pooled arrival rate comprising type 1 arrivals. This important result can be derived in a number of other ways, as well. Suppose that we are awaiting the first Poisson-type arrival and finally we are given the conditional information that the arrival occurred in the interval [t, t + dt]. Let 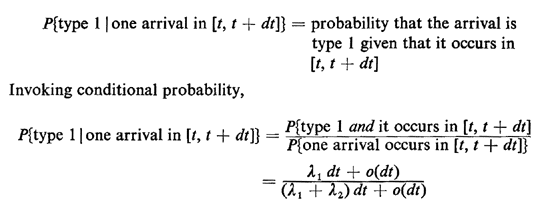
Since dt is infinitesimal, we can ignore the o(dt) term, thereby obtaining 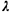 1/( 1/(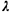 1 + 1 + 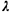 2)
for the conditional probability, conditioned on the infinitesimal arrival interval. We uncondition the probability by integrating over all possible arrival intervals, weighted by the probability
of their occurrence, 2)
for the conditional probability, conditioned on the infinitesimal arrival interval. We uncondition the probability by integrating over all possible arrival intervals, weighted by the probability
of their occurrence,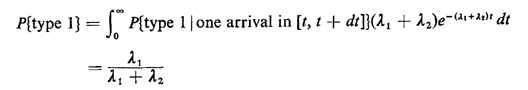
Yet a third way of deriving the result involves consideration of a long time period of length T. During that period the expected total number of arrivals is ( 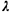 1 + 1 + 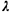 2))T; the expected number of type 1
arrivals is 2))T; the expected number of type 1
arrivals is 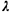 1T. Thus, roughly speaking, the fraction of total arrivals that is type 1 is 1T. Thus, roughly speaking, the fraction of total arrivals that is type 1 is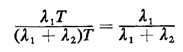
a result in agreement with the more formally derived (2.62). A final point about this result: in examining a Poisson process we occasionally only have to look at the arrival instants, distinguishing between, say, type 1 and type 2 arrivals, not caring about the exact times of their occurrence. Then, because of the no-memory property of Poisson processes, each arrival instant becomes an independent Bernoulli experiment, with probability of a type 1 arrival equal to 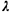 2/( 2/(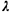 1 + 1 +
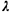 2) and of a type 2 equal to 2) and of a type 2 equal to 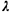 1/( 1/(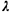 1 + 1 +
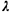 2). Thus, when considering questions of the types of Poisson arrivals
occurring (and not their times), we may invoke ideas of Bernoulli
experiments which often lead to geometric distributions, binomial
distributions, and other pmf 's associated with independent
discrete random variables. 2). Thus, when considering questions of the types of Poisson arrivals
occurring (and not their times), we may invoke ideas of Bernoulli
experiments which often lead to geometric distributions, binomial
distributions, and other pmf 's associated with independent
discrete random variables.We apply most of our results for a Poisson process to a "pedestrian crossing" problem at the end of the chapter. |


