First we discuss a situation in which the mean of a random
variable is obtained in an uncomplicated setting. Then we add
one or more complications that result in the addition of
perturbation terms to the original random variable. The question
of interest is: How do we find the mean of the random variable with
the added perturbation term(s)?
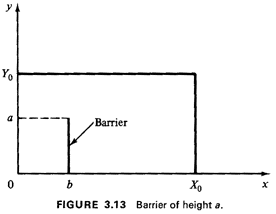
Example 6: Barriers to Travel
The method is illustrated by an example involving barriers to
travel. Suppose that we reanalyze the rectangular response
district (with a randomly placed response unit) described in
Exercise 3.1. We wish to discover how a barrier that impedes
travel increases the mean travel time. For convenience, we deal
directly with travel distance, which is assumed to be right-angle.
Solution
We again assume that the incident's position (X1, Y1) and
response unit's position (X2, Y2) are uniformly independently
distributed over the district. (In Exercise 3.1, the incident was
a medical emergency and the response unit was an
ambulette.) We know now that
E[D] = 1/3(X0 + Y0)
where the events Ai are mutually exclusive and collectively
exhaustive. In particular, consider the events
Thus, using (3.12) and (3.32)-(3.34), we have the desired result:
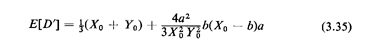
The second term on the right-hand side is the perturbation term.
To gain insight into the magnitude of the perturbation term,
suppose that we have a unit-area square district with a
barrier originating at a boundary halfway point,
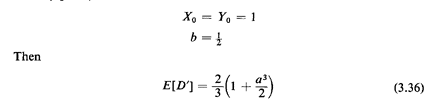
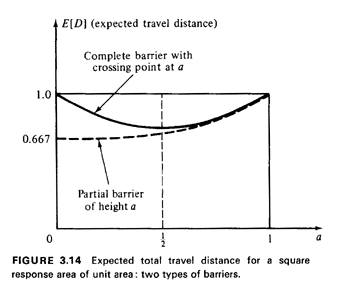
This function is plotted for 0 
a
1 in Figure 3.14. Note that a barrier of height a = 1/2, say, yields a mean travel distance
of 0.708, which is only about 6.3 percent greater than the mean
travel distance with no barrier (0.667).
We could use the same method to find the average travel distance
for the case of a barrier extending completely from y = 0 to y = Y0
with one crossing point at y = a (e.g., a river at x = b with a bridge at y = a).
The simplest way to do this is to add sequentially a second perturbation distance so that
D'' = D' + D'e
where D'e. is the extra distance traveled compared to the distance D'.
Exercise 3.2: River with One Bridge Using symmetry, show that for
this case (the complete barrier with one crossingpoint)
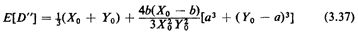
This function is also plotted in Figure 3.14.
The variance of D' in our original example is more difficult to
obtain due to "cross terms" between D and De.
Substituting directly into the definition of variance, we find
that
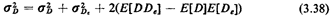
The variance of De is directly obtainable using the argument
above (solving first for E[D2e] by conditioning on the
event De > 0). However, the term in parentheses in general is not
equal to zero, because of the dependence between D
and D,. This dependence can be seen intuitively by considering
the conditional information De = 2a: then both
customer and server are located on opposite sides of the barrier
at y = 0 and D is (conditionally) distributed as
{(|X1 - X2|) | Min [X1, X2]
b, Max [X1,X2] > b}
rather than |X1 - X2 + |Y1 - Y2 (unconditioned).
Thus, while derivation of the variance presents no conceptual
problems, we will limit our work with perturbations to a
random variable to obtaining the mean of the new random variable.
We may summarize (and generalize) the approach as follows:
- Express the random variable of interest W' as the sum of an
easy-toanalyze (simple) random variable W and one or more
perturbation
random variables W'e, W''e....(The perturbation random variables
will usually have a positive probability of assuming the value zero.)
- Compute the mean of W' by summing the mean of the simple random
variable and the conditional means of each
perturbation random variable, given that it is positive,
multiplied by the probability that it is positive:
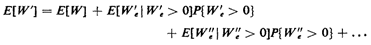
Further work: Problems 3.13-3.16,
