3.27 Circular city,
revisited Suppose
that two points (R1,  2)
and (R2, 2) are
independently, uniformly distributed over a circular city of radius
ro
and area A= 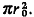 Suppose further that this city has a
large number of radial
routes and circular ring routes so that the travel distance between
(R1,
1)
and (R2, 2) can be
accurately approximated as
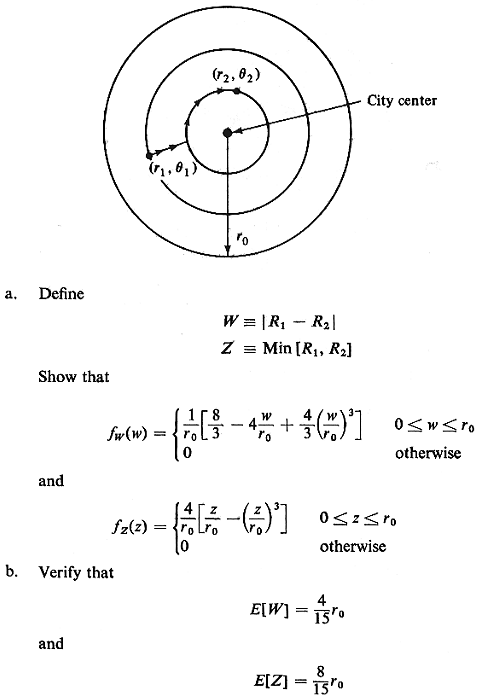
D = |R1 - R2| + Min [ R1, R2] |1
- 2|
where 0  |1 - 2|
 signifies
the magnitude of the angular difference between 1
and 2. In words,
travel from an outer point, say,
(R1,1)
if R, > R2, to an inner point
(R2,1)
first occurs along a radial route to a ring located a distance R2
from the city center,
and then along that ring (in the direction of minimum travel
distance) to (R2,1);
the same path is traveled in reverse if travel is from
(R2,1)
to (R1,1).
A sample path is shown in Figure P3.27.
and thus
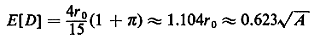
Compare this result to analogous results in
Problems 3.20 and 3.21.
|
