3.29 Effect of traffic lights on travel times  A vehicle travels a route from a to b, incurring a total travel time

T = 6 + W₁ + W₂   (minutes)

where     6 = time to traverse the distance (at constant speed) from a to b
           W₁ = delay incurred at traffic ight 1
           W₂ = delay incurred at traffic light 2

As shown in Figure P3.29, the route is partitioned into three 2-minute travel-time segments. Each traffic light operates on a fixed cycle of 1 minute green, followed by I minute red. (We assume that no time is wasted in decelerating and accelerating, should one or two lights cause the vehicle to stop.)

Suppose that exactly at some prespecified time (say 12: 00 noon) we examine the "phase"  _i, of each traffic light (i = 1, 2). By definition,

 _i = time until light i next turns to green (0 _i < 2)

For each light, we suppose that  _i, is independently, uniformly distributed over [0, 2]. However, once _i is known, its value isfixedfor all time.
    Throughout this problem, we assume that departure times at a occur independently of the phases of the traffic lights.

a. Find the mean and variance of the travel time from a to b.

b. Find the probability density function of the travel time from a to b.

c. Let k = number of traffic lights at which the vehicle is delayed. Find the z-transform of the probability mass function for k.

For parts (d) and (e), only [not for parts (f)-(h)], let

C = event that for the most recent vehicle traveling from a to b, the vehicle was stopped only at traffic light 1

d. Find the conditional joint probability density function for ₁ and ₂, given C.

e. Find the conditional probability density function for the travel time from a to b for the next vehicle to travel from a to b, given C. (Assume that you know nothing about when the next vehicle will leave a.)

For parts (f)-(h), suppose that vehicles leave a in a Poisson manner with mean 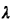= 1 vehicle per minute. Vehicles occupy zero space and, when in a traffic light queue, accelerate and decelerate instantaneously together.

f. Is the vehicle arrival process at b a Poisson process? Why or why not?

g. Determine the mean and variance of the queue length (number of vehicles) at traffic light I at the instant before the light turns green. (This is a primer for Chapter 4.)

h. A traffic engineer adjusts the phases of the two traflac lights so that ₁ = ₂ = 0 (relative to 12: 00 noon). Suppose that at 12: 00 noon we are given conditional information that no vehicles have left a during the last 8 minutes. Carefully sketch and label the probability density function for the time of arrival at b of the next vehicle to arrive there.