4.11 Time-Dependent Analysis of The M/M/m Queueing System
The applications of queueing theory that we have discussed so far in this chapter have
almost invariably used the assumption of steady state and thus have ignored the time
dimension. There are many situations, however, where it is precisely the fluctuation of
congestion effects with time that we are most interested in.
Consider, for example, the problem of
determining personnel requirements for the operation of toll booths at a bridge, tunnel,
or highway leading into a city. It would clearly be foolish to maintain the same number of
open booths from, say, 2 to 4 A.m. as during the peak traffic hours of 7 to 9 A.M. This
situation calls for an analysis that recognizes explicitly the fact that demand (i.e., the
rate at which cars arrive at the toll-collection area) varies considerably over time.
Similarly, in deciding on the number of police patrol units to be deployed over a 24-hour
period, a police administrator would do well to take into account the fact that the rate
of calls to police dispatchers is at a peak between 5 P.m. and midnight in most cities and
then falls rapidly to very low levels during the early morning hours.
One way to deal with such problems is to subdivide
the time period of interest into shorter time periods, during which the demand rates and
the service rates can be considered approximately constant and perform a separate queueing
analysis for each of these shorter time periods, assuming that the steady-state results
are valid within each of them. There are numerous examples of this type of analysis,
including a classical one [EDIE 54] that was applied to the toll-booth problem that we
have just described.
This approach, however, may sometimes be inadequate:
the demand and/or service rates may be changing too rapidly over time for the steadystate
expressions (which assume the existence of "long-term equilibrium conditions")
to be valid. The approach also fails if it happens that for one or more of the short
periods of time average demand exceeds the service rate-a case for which no steady-state
expressions exist.
In some cases of this type, numerical solution
techniques can often be of some help. We shall describe below one such technique as it
applies to M/M/m queueing systems.
The analysis below will be performed with reference
to the center-for-emergency-calls example (see Section 4.6), for which it will be assumed
that:
1. The arrival of calls at the M/M/m system is a Poisson process with a known
time-dependent rate 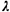 (t) for 0 (t) for 0  t t  T. T.
2. The m operators/servers are independent and identical, and service times
are independent and negative exponential with mean 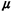  ( ( is not a function of time). is not a function of time).
3. The queueing system has a capacity of K (K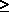 m) and calls that find the system full are
lost. m) and calls that find the system full are
lost.
4. The state of the system at time t = 0 is known probabilistically (see below
for further explanation).
Let Pn(t), i = 0, 1,
2, . . . , K, denote the probability that at time t there are n calls present-being
answered or waiting for an operator. Using the state-transition diagram 4.9, it is then
simple to write a system of first-order differential equations that describe this queueing
system [cf. (4.20) and (4.21)]:
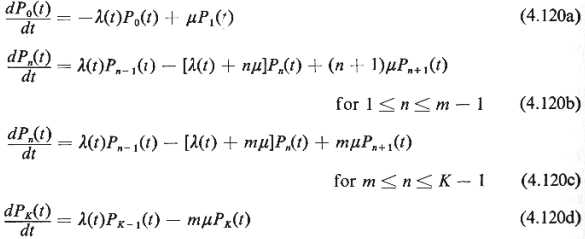
Given a set of probability values P(O) that describe the state of the queueing system
at t = 0 [i.e., P(0) ={P0(0), P1(0),
. . . Pk(0)} such that 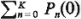 =1], the K +
1 equations (4.120) can be solved iteratively on a computer. To do this, one must choose a
time interval At which is sufficiently small to be consistent with the Poisson assumptions
for the arrival and service pro- cesses (i.e., the probability of two or more user
arrivals or service com- pletions during At must be very small) and then use the
approximation =1], the K +
1 equations (4.120) can be solved iteratively on a computer. To do this, one must choose a
time interval At which is sufficiently small to be consistent with the Poisson assumptions
for the arrival and service pro- cesses (i.e., the probability of two or more user
arrivals or service com- pletions during At must be very small) and then use the
approximation
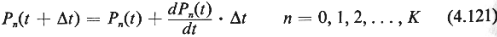
In this way, beginning with P(O), one first
solves for P( t)
= {P0( t)
= {P0( t), Pl( t), Pl( t), P2( t), P2( t),. . . , PK( t),. . . , PK( t)}, then for P(2 t)}, then for P(2 t), P(3 t), P(3 t), and so on,
for the whole period of interest T. This type of numerical solution can be accomplished
with the aid of standardized computer programs (such as the IBM Continuous System Modeling
Program-CSMP) which are designed specifically for accurate iterative solution of systems
of differential equations such as (4.120). t), and so on,
for the whole period of interest T. This type of numerical solution can be accomplished
with the aid of standardized computer programs (such as the IBM Continuous System Modeling
Program-CSMP) which are designed specifically for accurate iterative solution of systems
of differential equations such as (4.120).
Once the probabilities Pn(t)
have been computed, other quantities of interest can be derived as well. For instance, for
the expected number of calls in queue at time t, we have
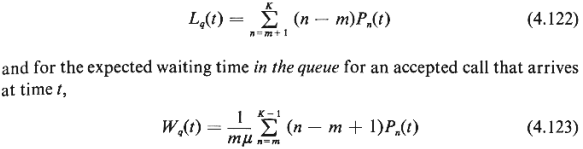
Exercise 4.7 Argue the validity of (4.123). Why not use the expression
Wq(t) = Lq(t)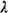 (t) in this case? (t) in this case?
In urban problems, the foregoing
time-dependent queueing model arises most often in situations where the demand rate, 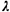 (t), is
periodic with period (t), is
periodic with period  = 24 hours.) This, for example, would be the case for the
toll-booth and police-allocation problems described at the beginning of this section. In
that case it is reasonable to expect and it has been shown [KOOP 72] that
the numerical solution of (4.120) will also become periodic eventually, independent of the
starting conditions P(0), as long as 17 = 24 hours.) This, for example, would be the case for the
toll-booth and police-allocation problems described at the beginning of this section. In
that case it is reasonable to expect and it has been shown [KOOP 72] that
the numerical solution of (4.120) will also become periodic eventually, independent of the
starting conditions P(0), as long as 17
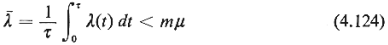
In that case, we shall have Pn(t
+  ) = Pn(t)
for all t greater than some threshold value. For relatively low utilization
systems, the probabilities P,(t) will converge to the periodic solution very quickly
(e.g., after a few hours of the first day when ) = Pn(t)
for all t greater than some threshold value. For relatively low utilization
systems, the probabilities P,(t) will converge to the periodic solution very quickly
(e.g., after a few hours of the first day when  = 24 hours.) Convergence, however, cannot be
verified until (4.120) have been solved for a second (or third, or more, if necessary)
day. = 24 hours.) Convergence, however, cannot be
verified until (4.120) have been solved for a second (or third, or more, if necessary)
day.
Although, in order to obtain numerical solutions of
(4.120) one must naturally have a finite number (= K + 1) of equations, one can still use
a trial-and-error approach to obtain solutions for cases where no calls/users can be
turned away [provided that (4.124) holds]. All one has to do is specify K to be
sufficiently large so that at no time does Pk(t),
the probability of a full system, exceed some acceptable value [e.g., Pk(t)
< 10-4 for all t]. Problems with K as high as 600 have been solved at
reasonable computer cost [HENG 75]. An application of the M/M/m time-dependent model to
the deployment of police patrol cars through the day in New York City is described in
[KOLE 75].
17 If (4.124) does not hold, the queueing system will eventually become
saturated.
|