4.2 BACKGROUND, TERMS, AND SOME CONVENTIONAL NOTATION
In this chapter we shall use the term queueing system to refer to
a generic model (see
Figure 4.1) which comprises three elements: a user source, a queue,
and a service facility
that contains one or more (including possibly an infinite number of)
identical servers in
parallel. Thus, each user of a queueing system is
"generated" by a user source,
passes through the queue where (s)he may remain for a nonnegative
period of time
(including possibly zero time), and then is processed by a single
server-because of the
parallel arrangement of servers. Once a user has left any one of the
servers in the
system, after obtaining service there, the user is considered to
have left the queueing
system as well.
In view of the description given above, a queueing network can
now be defined as a set
of interconnected queueing systems. Thus, in a queueing network, the
user sources for some
of the queueing systems in the network may be other queueing systems
in the same network
(see also Figure 4.2). It can also be inferred that the analysis of
models of queueing
systems, as we have defined them here, provides the building blocks
for the analysis of
queueing networks.
To describe a queueing system fully, information must be supplied
about all three
generic elements of the system (Figure 4.1):
About the user generating process (i.e., the arrival
process of users at the
system).
About the queue discipline [i.e., the order in which users
obtain access to the
service facility, once (and if) they join the queue].
About the service process.

To describe a queueing network, further
information must be provided
(Figure 4.2) on how the queueing systems are interconnected, how
they interact (e.g., do
bottlenecks "downstream" ever affect the preceding
servers?), and how users are
assigned to the queueing systems.
It should be obvious that there exist countless
variations of queueing
systems and networks. We shall have occasion to refer to some of
these variations in
following sections. At this point, however, it should be noted that
a code has been used
in queueing theory for years to describe some of

the simplest (and best understood) queueing systems. This code is
of the form A|B|m,
where A and B are letter symbols and m is an integer constant. The
letters A and B
indicate the probability distribution of user interarrival times and
of service times,
respectively, and m is the number of identical parallel servers in
the queueing system
(thus, m can take values from 1 to 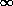 ). ).
The standard code letters used for probability
distributions in
queueing theory are:
M = Poisson (i.e., negative exponential pdf for user
interarrival times or for service
times; M stands for "memoryless")
D = deterministic (i.e., interarrival or service times are
constant)
Ek = kth-order Erlang distribution [see (2.50) and
(2.57)]
Hk = kth-order hyperexponential distribution (see
Problem 4.6)
G = "general" distribution (i.e., any distribution at
all)
The letters A and B can thus be any one of the five symbols
above.
To newcomers to queueing theory it always seems
strange that, out of
all possible probability distributions, only four (M, D,
Ek, and Hk)
have been assigned special symbols. The simple reason is that only
these four
distributions offer significant advantages in an abstract analysis,
in the sense that when
they are present in a queueing model, parts of the mathematical
analysis of that model may
become more tractable. Thus, all other distributions are lumped
under the
"general" (G) category (which, of course, also includes
the M, D, E, and Hk
cases). These comments will become more clear as we make our way
through this chapter.
The coded systems also assume independence of
successive user arrival
times and of successive service times at the queueing system. We
shall see several
examples of urban service systems where this assumption is not valid
in practice.
Some more-or-less standard abbreviations are also
used to indicate the
most commonly encountered queue disciplines. FIFO is used to
indicate the first-in,
first-out queueing arrangement, also known as FM first come, first
served). Similarly,
LIFO (= last in, first out) or LCFS last come, first served)
indicate the situation in
which the last user to join the queue becomes the next in line for
entering service. The
abbreviation SIRO is used to indicate "service in random
order." Although LIFO
and SIRO may at times appear offensive to our sense of
fairnessespecially in connection
with gaining access to public transportation vehicles during peak
traffic hours-they, and
their variations are all too common in real life and thus cannot be
ignored.
Another important parameter in the description of
a queueing system is
the system capacity. This indicates the maximum number of
users that can at any
time be in the service facility and in the queue. Queue
capacity, on the
other hand, indicates the maximum number of users that can be in the
queue alone.
Finally, it is important to emphasize that
queueing systems need not
adhere to the classical picture of a physically stationary server (a
bank teller, a
checkout counter, highway toll booths, etc.) where prospective users
queue up to be
served. It is very common to have systems in which the prospective
users remain
stationary, possibly at geographically widely separated points,
while the server(s)
associated with the queueing system visit them according to some
(implicit or explicit)
priority scheme and provide the requested service. We often use the
term spatially
distributed queues to refer to such geographically
"spread-out" systems.
They are of particular interest in urban operations research and
Chapter 5 will deal with
their specific characteristics. For some of these systems (e.g.,
fire departments or
ambulance services), queues in the sense of a backlog of calls for
service, rarely, if
ever, occur. Yet queueing theory is most valuable in planning for
such systems-in
determining, for instance, the number of vehicles needed, the
expected workload of service
units, or the best deployment of the service units in a city. |