4.8.3 G/G/1 System
We consider next a system
consisting of a single
server with independent and identically distributed user
interarrival times, independent
and identically distributed service times and unlimited queueing
capacity. This is the
G/G/1 system.
Let us now call X the random
variable that represents
interarrival time and use fx(x), 1/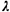 , and , and 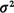 x for
the pdf, the expected
value and the variance of X, respectively. Similarly, as we have
already done, we shall
use S, fs(s), 1/ x for
the pdf, the expected
value and the variance of X, respectively. Similarly, as we have
already done, we shall
use S, fs(s), 1/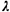 , and , and 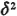 s as the corresponding
symbols for the service
times. s as the corresponding
symbols for the service
times.
Practically no easily usable
exact results exist for
this model because of the analytical difficulties that we outlined
earlier. However, some
useful bounds have been developed in recent years for the quantities
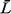 , , 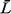 q, q, 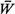 and and 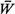 q. q.
For general G/G/1 systems
(no restrictions on
the interarrival or on the service time pdf's) a most useful upper
bound [MARS 68] and a
(much less useful) lower bound [MARC 78] have been obtained.
These bounds state that
for the average steady-state waiting time in queue, 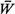 q, we have q, we have
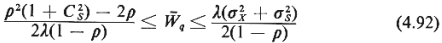
where Cs (= 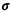 s s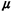 ) is the coefficient of variation for the
service times [as used
in (4.79a)] and, as usual, ) is the coefficient of variation for the
service times [as used
in (4.79a)] and, as usual, 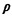 = = 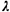 / /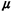 . The condition for the existence of steady
state is . The condition for the existence of steady
state is 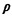 < 1. < 1.
That the lower bound in
(4.92) is not
particularly tight becomes obvious from the fact that, even at very
high utilization rates
(p  1),
this bound is trivial (i.e., takes negative values) unless
Cs > 1. But for Cs,
to be greater than 1, it must be that the service time pdf must be
"more random"
than the negative exponential pdf (which has Cs = 1).
This would be rather
unusual in practical urban service system problems. 1),
this bound is trivial (i.e., takes negative values) unless
Cs > 1. But for Cs,
to be greater than 1, it must be that the service time pdf must be
"more random"
than the negative exponential pdf (which has Cs = 1).
This would be rather
unusual in practical urban service system problems.
Fortunately, a simple and
quite tight lower
bound has been obtained [MARS 68] for a particular subclass of G/G/1
queueing systems.
This subclass, happily, encompasses most of the cases that one is
likely to encounter in
practice. The subclass of G/G/1 queueing systems that we refer to
consists of those
systems for which the interarrival time pdf
fx(x) has the
following property: For all values of a constant to (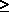 0), it is true
that 0), it is true
that
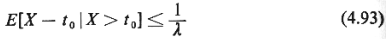
Although (4.93) may appear complicated at first sight, it really
imposes a very simple
condition: if it is known that any given interarrival gap lasted
more than a time
t0,
then (4.93) requires that the expected length of the
remaining time, X -
t0,
in that gap be less than the unconditional expected length of the
gap, *10
E[Xl (= 1 /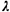 ). One of the basic properties of the
negative exponential
random variable, as we know, is that (4.93) is an equality for this
random variable. ). One of the basic properties of the
negative exponential
random variable, as we know, is that (4.93) is an equality for this
random variable.
When condition (4.93) is
satisfied, the
following is true:
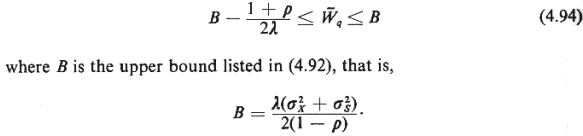
As usual, the
relationships  , = , =   q, q,
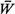 = = 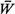 q
+ 1/ q
+ 1/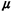 , and , and 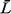 = = 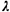 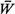 hold, and thus
upper and lower bounds can be obtained for the quantities hold, and thus
upper and lower bounds can be obtained for the quantities 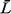 , , 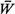 , and , and 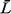 q,
as well from the
bounds above. To appreciate how good the bounds in (4.94) are, we
can look at the form
that (4.94) takes for the average queue length, q,
as well from the
bounds above. To appreciate how good the bounds in (4.94) are, we
can look at the form
that (4.94) takes for the average queue length, 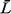 q.
We have q.
We have
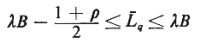
which means that the difference between the upper and the lower
bounds is (1 + 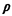 )/2,
and since 0 < )/2,
and since 0 < 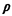 <
1, this difference is
always between 1/2 and 1. loprobability distributions
that have this
property are sometimes referred to as Mecreasing mean residual
life" (DMRL)
distributions, for obvious reasons. Thus, we are able to determine
the average queue
length to within an accuracy of between 0.5 and 1 user (depending on
the value of <
1, this difference is
always between 1/2 and 1. loprobability distributions
that have this
property are sometimes referred to as Mecreasing mean residual
life" (DMRL)
distributions, for obvious reasons. Thus, we are able to determine
the average queue
length to within an accuracy of between 0.5 and 1 user (depending on
the value of 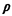 ),
which is truly excellent
for any practical application. In fact, the two bounds, remarkably,
get closer to each
other, on a percentage basis, as ),
which is truly excellent
for any practical application. In fact, the two bounds, remarkably,
get closer to each
other, on a percentage basis, as 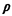 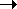 1, because 1, because 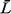 q
then becomes large, and
a difference of 1 between the two bounds is thus insignificant. q
then becomes large, and
a difference of 1 between the two bounds is thus insignificant.
It has already been
stated that the case which
satisfies condition (4.93) and, consequently, for which tight upper
and lower bounds can
be used is the most common in practice. The reason is that most
"well-behaved"
arrivaltime distributions satisfy (4.93). Such, for instance, would
be the case for
uniform or triangular or beta-type pdf's, which often are reasonably
good approximations
of many general interarrival time pdf's. Only a few common
continuous random variables,
notably those in the hyperexponential family, which are "more
random"-informally
speaking-than the negative exponential random variable (see Problem
4.16), do not, in
fact, satisfy (4.93). In practice, it is usually simple to recognize
those distributions
which do not satisfy (4.93). This is especially true of random
variables taking on
discrete values only.
Consider, for instance,
the random variable Y
with the probability mass function shown in Figure 4.14. For the
value t0
= 1, we have
E[Y-t0
| Y
> t0] = E[Y
> 1] = P{Y=10*(10-1)
=1.9 = 9
On the other hand, E[Y1 = 1. 1 + 1. 10 = 5.5. Therefore, (4.93) is
not satisfied
by random variable Y.

Heavy-traffic approximation. Another
important practical result
which is available for the G/G/1 system is known as the
heavy-traffic approximation
[KING 62]. As the name suggests, this is a result that applies for
values of p
which are close to 1 and, consequently, it provides estimates for
waiting times when it is
known that waiting times are large.
The heavy-traffic approximation states that when p 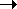 1, the
distribution of steady-state
waiting time in queue in a G/G/1 system is approximately negative
exponential with mean
value 1, the
distribution of steady-state
waiting time in queue in a G/G/1 system is approximately negative
exponential with mean
value
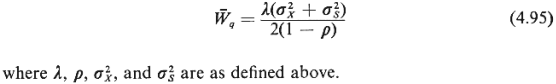
This is a remarkable
result, since it
provides not just an estimate of a moment of waiting times but of
the actual distribution
itself under very general conditions.
Note that the above
expression for 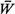 q
is identical to the expression for the upper bound on ITV, for
G/G/1 systems in (4.92).
Thus, the upper bound of (4.92) improves as an approximate
estimate of q
is identical to the expression for the upper bound on ITV, for
G/G/1 systems in (4.92).
Thus, the upper bound of (4.92) improves as an approximate
estimate of  q
as p q
as p  1.
From (4.95) and (4.94) we can also reach the following important
practical conclusion: 1.
From (4.95) and (4.94) we can also reach the following important
practical conclusion:
The average waiting time for G/G/1 queueing systems becomes
dominated by a (1 - p)-1
term under steady-state conditions, as the utilization ratio
approaches 1. Thus, the type
of behavior first indicated by the simple M/M/1 queueing system is
also present for
entirely general arrival- and service-time distributions.
|