|
5.8 Three-server queue: evaluating a new technology A
certain
circular highway is patrolled by three public safety cars. Each car
patrols a 1-mile sector of the 3-mile highway (see Figure P5.8). Calls
for assistance occur along the highway. A dispatcher assigns a car to
each call, if at least one is available. We wish to examine various
operating properties of this system.

The system operates as follows:
- Call positions are uniformly, independently distributed over the
circular highway.
- The call arrival process is a homogeneous Poisson process with
rate parameter
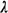 calls per hour. calls per hour.
- Service time at the scene of the call has a negative exponential
distribution with mean
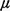 -1 = ½
hour. -1 = ½
hour.
- Travel time is negligibly small compared to service time at the
scene.
- Speed of response is always 30 miles/hr.
- U-turns are permissible everywhere.
For parts (a)-(c), assume that the dispatching strategy is as
follows. Given a call from sector i (i = 1, 2, 3):
- Assign car i, if available.
- Otherwise, randomly choose some car j (j
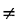 i), and assign it, if at least one other
car is available. i), and assign it, if at least one other
car is available.
- Otherwise, the call is lost.
- Find the steady-state probability that i cars are busy
(i = 0, 1, 2, 3).
- Find the steady-state probability that car 1 is busy and car 2 is
free.
- Find the average travel time to calls for this system. Evaluate
for
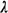 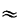 0, 0, 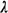 = 3, = 3, 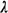 = 1,000. = 1,000.
- It has been proposed that the public safety bureau should
purchase a perfect resolution car locator system. With such a system,
the dispatching strategy is changed as follows:
Given a call from sector i (i = 1, 2, 3):
- Assign the closest available car, if at least one is
available;
- Otherwise, the call is lost.
Find the average travel time to a call for this system. Evaluate for
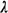 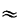 0, 0, 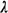 = 3, = 3, 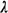 = 1,000. (This
part will utilize your knowledge of geometrical probability concepts.) = 1,000. (This
part will utilize your knowledge of geometrical probability concepts.)
|



