6.1 DEFINITION OF TERMS AND NOTATION
The terms network and graph will be used interchangeably to refer to
an entity G(N, A) consisting of a finite set, N. of nodes (or vertices)
and a finite set, A, of edges (or arcs or links or branches) which
connect pairs of nodes. An edge connecting nodes i 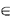 N and j
N and j 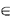 N will be
denoted as (i, j). If every edge has a specified orientation, the graph
is called directed (or oriented); if no edge has an orientation, the
graph is undirected (or nonoriented); and if some edges are directed and
some are not, the graph is mixed. A directed edge (i, j) leads from i to
j (see also Figures 6.1 and 6.2). N will be
denoted as (i, j). If every edge has a specified orientation, the graph
is called directed (or oriented); if no edge has an orientation, the
graph is undirected (or nonoriented); and if some edges are directed and
some are not, the graph is mixed. A directed edge (i, j) leads from i to
j (see also Figures 6.1 and 6.2).
An edge is incident on the two nodes it connects. Any two nodes
connected by an edge or any two edges connected by a node are said to be
adjacent. The degree of a node in an undirected graph is the number of
edges incident on it; for directed graphs the indegree of a node is the
number of edges leading into that node and its outdegree, the number of
edges leading away from it (see also Figures 6.1 and 6.2).
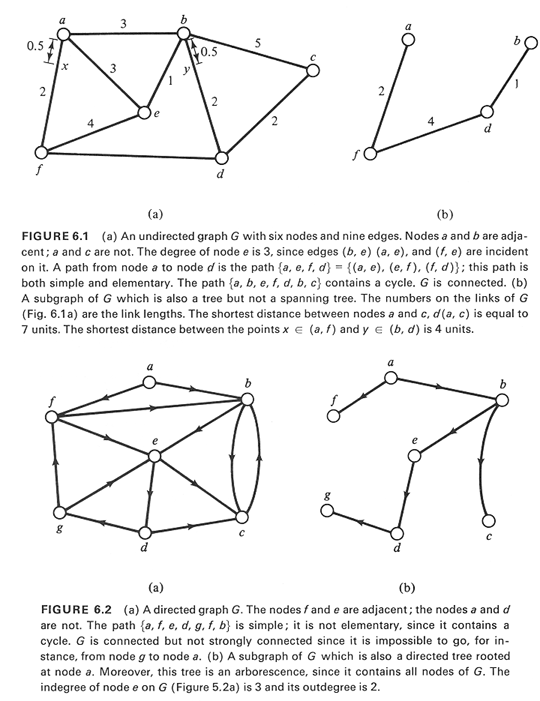
A path (or chain) on an undirected graph is a sequence of adjacent
edges and nodes. In a directed network, paths are directed as well, with
adjacent edges leading into and away from successive nodes. Paths can be
indicated as sequences of adjacent nodes (e.g., S = {a, b, c, . . ., i,
j, k}) or of adjacent edges [e.g., S = {(a, b), (b, c), . . ., (i, a),
(j, k)}]. A path is simple if each edge appears only once in the
sequence and it is elementary if each node appears
only once in the sequence. A cycle (or circuit) is a path whose initial
and final nodes coincide (see also Figures 6.1 and 6.2).
Related to the concept of a path is the concept of network
connectivity. A node i is connected to a node j if there exists a path
leading from i to j. A connected undirected graph is one for which a
path exists between every pair of nodes i, j 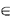 N. Similarly, a directed
graph is connected if its associated undirected graph (i.e., the graph
that results if orientation is removed from its edges) is connected.
Note that in a connected directed graph no path may exist leading from
some node i to some other node j (i.e., i is not connected to j).
However, in the case of a strongly connected directed graph, a path
exists between all ordered pairs of nodes (i.e., from every node i
N. Similarly, a directed
graph is connected if its associated undirected graph (i.e., the graph
that results if orientation is removed from its edges) is connected.
Note that in a connected directed graph no path may exist leading from
some node i to some other node j (i.e., i is not connected to j).
However, in the case of a strongly connected directed graph, a path
exists between all ordered pairs of nodes (i.e., from every node i
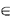 N
to every other node j N
to every other node j 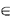 N. and vice versa) (see also Figures 6.1 and
6.2).
N. and vice versa) (see also Figures 6.1 and
6.2).
A subgraph G'(N', A') of a graph G(N, A) is a graph such that2
N' 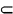 N and A' N and A' 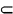 A. A' can only contain arcs whose end points are
in N'. A tree of an undirected network is a connected subgraph that has
no cycles. Thus, a connected tree with t nodes has exactly t-I edges and
there exists a single path between any two nodes on the tree. A spanning
tree of a graph G(N, A) contains the complete set N of the nodes of G.
For directed graphs, a directed tree has a root node and a unique path
from that node to every other node in the tree. An arborescence of a
directed graph G(N, A) is a directed tree that contains the complete set
N of the nodes of G (see also Figures 6.1 and 6.2).
A. A' can only contain arcs whose end points are
in N'. A tree of an undirected network is a connected subgraph that has
no cycles. Thus, a connected tree with t nodes has exactly t-I edges and
there exists a single path between any two nodes on the tree. A spanning
tree of a graph G(N, A) contains the complete set N of the nodes of G.
For directed graphs, a directed tree has a root node and a unique path
from that node to every other node in the tree. An arborescence of a
directed graph G(N, A) is a directed tree that contains the complete set
N of the nodes of G (see also Figures 6.1 and 6.2).
In a network problem, a number of node or link characteristics are
usually specified. Most commonly, a length is associated with every link
of G. where "length" can be in units of distance, time, money, and so
on. Link lengths will be indicated as 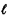 (i, j), where (i, j)
(i, j), where (i, j) 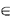 A. The
length of a path, S. between two nodes on G is then given by L(S) = A. The
length of a path, S. between two nodes on G is then given by L(S) =
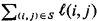 . We shall use the notation d(x, y) to indicate the
shortest distance between two points x, y . We shall use the notation d(x, y) to indicate the
shortest distance between two points x, y 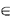 G. Note that x and y are not
restricted to be members of the node set of G but can be any two points
on G. We shall often use the notation d(i, j) to indicate the shortest
distance between points which belong to the node set N of G (see also
Figures 6.1 and 6.2). G. Note that x and y are not
restricted to be members of the node set of G but can be any two points
on G. We shall often use the notation d(i, j) to indicate the shortest
distance between points which belong to the node set N of G (see also
Figures 6.1 and 6.2).
Some further notational conventions will be introduced as they become
necessary later in this chapter.
2 The notation A 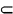 B indicates that a set A is
contained in a set B. This includes the possibilities that A = B indicates that a set A is
contained in a set B. This includes the possibilities that A =  , the
null set, and that A = B. , the
null set, and that A = B.
|



