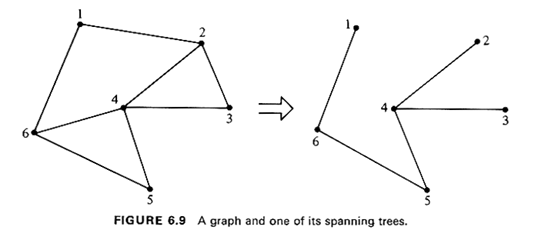
6.3 MINIMUM-SPANNING-TREE PROBLEM

A spanning tree of an undirected graph G(N, A) has already been defined as a tree of the graph G that contains the complete set of nodes, N, of G (see also Figure 6.9). The minimum-spanning-tree problem is then concerned with finding the one among all possible spanning trees of a graph G(N, A) with the minimum total link length. If the number of nodes in the set N is n, then all spanning trees of G obviously contain n - 1 links.

Just as in the case of shortest-path problems, the minimum-spanning-tree (MST) problem has direct applications of its own, primarily in problems of transportation network design, and also constitutes an important building block in some solution approaches to other more complex problems such as node-covering problems (see Section 6.4). For a brief example of an application of the MST problem, consider the case in which map locations of n rural towns are given along with a matrix listing the Euclidean distances (or some other measure of distance, time, or cost) between all possible pairs of towns. The MST can be interpreted in this case as the minimum length of roads needed to connect, directly or indirectly, all pairs of towns, assuming that all road segments (links) begin and end in some pair of towns.

The last sentence emphasizes the distinction between the MST problem and the so-called "Steiner problem." The latter has the same objective as the former but allows the introduction of artificial "nodes" (i.e., links can meet anywhere on the plane instead of only at the specified points that are to be spanned). To illustrate this further, consider four towns that lie at the corners of a unit square. Obviously, one solution to the MST problem in this case is the one shown in Figure 6.10a; the total length of the minimum spanning tree is 3 units. On the other hand, it can be shown that if creation of artificial nodes is permitted (Steiner,s problem), the total line length needed to connect the four points can be further reduced. The solution to Steiner's problem in this case is shown in Figure 6.10b and involves creation of two artificial nodes (A and B in Figure 6.10b); the total length of the Steiner tree is 1 + 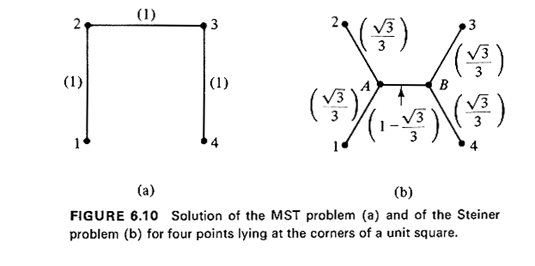in this case.