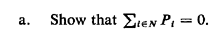|
6.6 Chinese postman problem on a directed network To solve
the CPP on a directed network [BELT 74], we begin by quoting the version of
Euler's theorem that applies to directed networks:
A connected directed network possesses an Euler tour if and only
if the indegree and the outdegree of every one of its nodes are equal.
The proof of this theorem is completely analogous to the proof of Euler's
theorem for undirected networks (you may wish to retrace its steps).
To solve the CPP on any directed graph, we first define
Pi = "polarity" of i = (indegree of i) - (outdegree of i)
A node i for which Pt > O (Pi < o) is called
a "supply" ("demand") node. we indicate the sets of supply and demand nodes
as s and d, respectively.
The following algorithm solves the CPP on directed graphs (the algorithm
is stated informally):
| STEP | 1:
| Identify all supply and demand nodes and compute the polarities of
each and the minimum distanced (i,j) from all nodes i  S to all nodes j
S to all nodes j 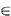 D. D.
| | STEP | 2:
| Solve a transportation problem (TP) to find the optimum "matchings"
of supply with demand nodes. This TP is:
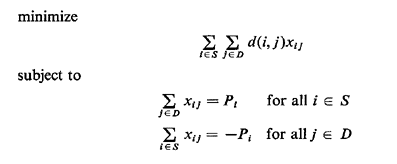
| | STEP | 3: | For
each xij > O in the solution to the TP, add to G, xij
replications of the shortest path from i 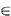 S to j S to j 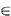 D. The resulting network
G' has Pi = O for all nodes.
D. The resulting network
G' has Pi = O for all nodes.
| | STEP | 4: | Find
an Euler tour on G'. This tour is a solution to the CPP on G.
|
| b. | Write a paragraph explaining what
the algorithm above does and why. Can any links be traversed more than
twice in the CPP solution?
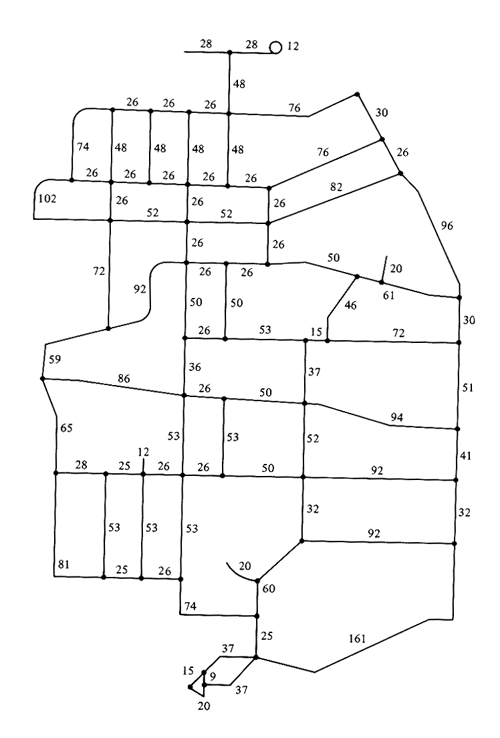
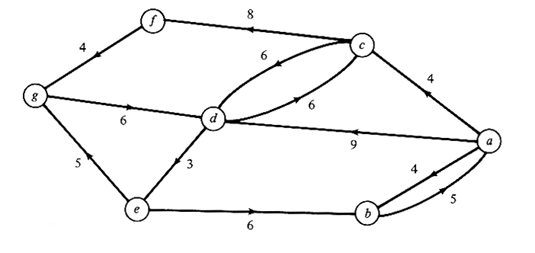
| | c. | Apply the algorithm above to solve
the CPP on the directed network of Figure P6.6. Describe a minimum-length
tour that begins and concludes at node b.
Hint: The optimal solution requires coverage of 28 units of
distance over and above the length of the network.
| | d. | Suppose now that G is a mixed graph
(i.e., it has both directed and undirected links). It might be thought that
in order to solve the CPP on such a network one could (1) substitute all
undirected links (i, j) with two directed links (i, j) and (j, i) of equal
length (and of opposite directivities); and (2) apply the algorithm
(for the CPP on directed graphs) described above to the resulting directed
network. What is wrong with this approach? As we noted earlier in the
chapter, no efficient algorithm is available for the CPP on mixed graphs and
the problem has in fact been shown to be NP-complete.
|
|