7.2.5 Intersections of Reporting Zones

It will be assumed below that all geographical entities under consideration are simple polygons. A simple polygon is one that has no intersecting sides (see Figure 7.20a). It is easy to check whether this condition is satisfied by using Algorithm 7.1. For an n-sided polygon, each side is viewed as a line segment and Algorithm 7.1 is applied. If no intersections are discovered, the polygon is simple. If it is not, the polygon can be viewed as a chain of two or more simple polygons, with neighboring polygons in the chain having only a finite number of corner points in common (Figure 7.20b). Each simple polygon in the chain can then be treated separately. Thus, the assumption that all geographical entities are simple polygons is not restrictive.

An important issue now is deciding whether two simple polygons A and B overlap.₈ For this to happen, either some sides of A must intersect some sides of B, or A must be wholly contained in B (or vice versa). The following procedure then suggests itself. We shall assume, without loss of generality, that polygons A and B are both n-sided.

STEP 1:	Treat the 2n sides of the two polygons as 2n line segments and apply Algorithm 7.1. If an intersection is discovered,9 the two polygons must overlap, since each polygon is simple (and thus its n sides do not intersect). If no intersections are discovered, proceed to Step 2.
STEP 2:	Take any corner point of polygon A and, using the point-polygon method, decide whether that point is contained in polygon B. If it is, polygon A is also entirely contained in B (and thus the two overlap). If it is not, take any corner point of B and, using the point-polygon method, decide whether that point (and thus B as well) is contained in A. If it is not, polygons A and B do not overlap.

Since in Step 1 we have 2n line segments, and thus 4n end points, the time required is O(n log₂ n). The point-polygon method (and Step 2) is O(n). It follows that it is possible to decide whether two n-sided polygons (or reporting zones, districts, etc.) overlap in O(n log₂ n) time.

We can now answer the question which we posed earlier. To find which ambulance zones have areas in common with a particular police precinct, we apply the procedure described above k times (where k is the number of candidate ambulance zones), once for each ambulance zone. If both the police precinct and the ambulance zones are n-sided polygons, this question can be answered in O(kn log₂ n) time.

So far we have been able to check whether zones overlap with each other and, if so, to identify the pairs of zones that overlap, as well as whether the overlap is partial or if one zone is fully included in another (and which one). It is also possible to identify the polygon that forms the intersection of two overlapping zones (i.e., to have the computer "draw" this intersection for us). 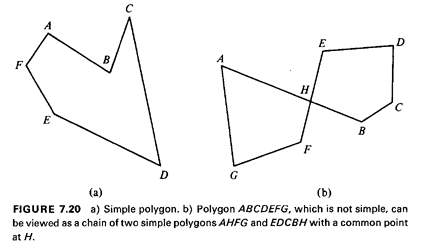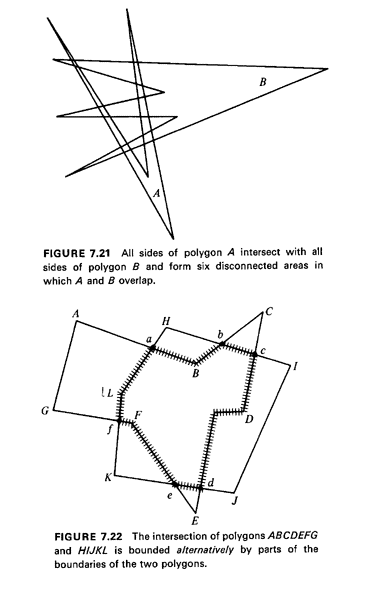Unfortunately, however, there are no shortcuts for doing this faster than the straightforward method: since, in the worst case, each side of polygon A will intersect every side of B (and vice versa), there will be a total of n² intersections (if A and B are n-sided polygons), and therefore the computational effort must also be at least O(n²)- see also Figure 7.21. It should be noted that the boundary of the polygon that describes the intersection of two polygons A and B consists of a part of the boundary of polygon A, followed by a point where a side of A intersects with a side of B, followed by a part of the boundary of B, followed by an intersection point of the boundaries, followed by a part of the boundary of A, and so on (see Figure 7.22). This, of course, assumes that A is not fully contained in B, or vice versa.