Vectors Don't have a Location

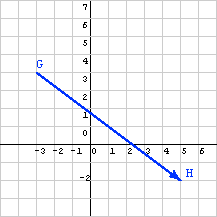
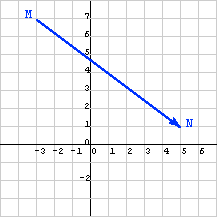
Now calculate the displacement from M to N in the diagram on the right. Subtracting values of the start N from corresponding values of the finish M gives: (8, -6)^T. This is the same as for the first diagram.

Geometrically, the displacement vector from G to H is the same as the displacement vector from M to N. Using the rule for column matrix equality (to review it, click here) the two column matrices are equal. This makes sense because in walking from point G to H you go the same distance and direction as in walking from M to N. The diagrams show the displacements with the same length and direction (but different starting points):

Vectors have no location. In a diagram it is common to draw a vector as an arrow with its tail on one point and its tip on another point. But any arrow with the same length and direction represents the vector.