Solving for kv

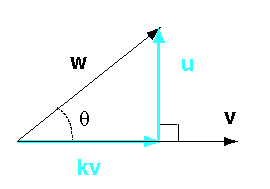
We want:   w = kv + u,   with the condition that u is orthogonal to v. Using trigonometry:

The length of kv  =   | w | cos

The orientation of kv is v_u

Remember that unit vectors are used to represent orientation in 3D space. The orientation of v is v_u. (In the picture, this happens to be horizontal, but that is just for convenience). Since cos θ is w_u · v_u, we have what we need:

kv  =  |w| (w_u · v_u) v_u

This formula may look awful, but it is not. This part:

|w| (w_u · v_u)

is a scalar. It adjusts v to to required length. In the picture this is the length of the horizontal baby blue line.

The remaining part:   v_u,   just says, "same orientation as v."