Will the results of this chapter work when vectors are represented
with column matrices?
Example
Time for an example.
In the diagram the answer can simply be read off the
graph paper.
But pretend you didn't notice that.
The vector w is represented by by (6, 5)T.
The vector v is represented by by (9, 0)T.
Find kv and u.
- Compute the lengths:
- | w | =
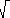 ((6, 5)T·(6, 5)T) = 7.81 ((6, 5)T·(6, 5)T) = 7.81
- | v | =
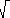 ((9, 0)T·(9, 0)T) = 9 ((9, 0)T·(9, 0)T) = 9
- Compute the unit vectors:
- wu = (6, 5)T / 7.81
- vu = (9, 0)T / 9 = (1, 0)T
- Compute the cosine of the angle between the vectors:
- wu · vu
= (1/7.81) (6, 5)T · (1, 0)T
= 6/7.81
- Assemble the projection:
- kv = | w | (wu·vu) vu
- kv = 7.81 (6/7.81) (1, 0)T
= 6(1, 0)T = (6, 0)T
- Compute the orthogonal vector:
- u = w - kv
- u = (6, 5)T - (6, 0)T = (0, 5)T
|
|
The result is that u = (6, 0)T + (0, 5)T,
as expected.
Of course, the example was easy.

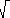 ((6, 5)T·(6, 5)T) = 7.81
((6, 5)T·(6, 5)T) = 7.81