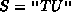Design and implement a MultipleStack class
which provides 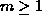 stacks in a single container.
The declaration of the class should look something like this:
stacks in a single container.
The declaration of the class should look something like this:
class MultipleStack : public Container
{
// ...
public:
MultipleStack (unsigned int);
void Push (Object&, unsigned int);
Object& Pop (unsigned int);
// ...
};
-
The constructor takes a single integer argument
that specifies the number of stacks in the container.
-
The Push function takes two arguments.
The first gives the object to be pushed
and the second specifies the stack on which to push it.
-
The Pop function takes a single integer argument
which specifies the stack to pop.
Choose one of the following implementation approaches:
-
Keep all the stack elements in a single array.
-
Use an array of Stack objects.
-
Use a linked list of Stack objects.
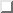 .
.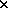 and
and  .
.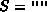 , i.e., S is the string of length zero,
, i.e., S is the string of length zero,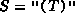 ,
,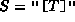 ,
,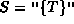 ,
,