Applications

Data Structures and Algorithms with Object-Oriented Design Patterns in C++

Applications

Section shows how a stack can be used to compute the value of a postfix expression such as

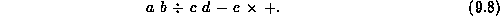
Suppose instead of evaluating the expression we are interested in constructing the corresponding expression tree. Once we have an expression tree, we can use the methods described in Section 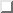to print out the expression in prefix or infix notation. Thus, we have a means for translating expressions from one notation to another.

It turns out that an expression tree can be constructed from the postfix expression relatively easily. The algorithm to do this is a modified version of the algorithm for evaluating the expression. The symbols in the postfix expression are processed from left to right as follows:

If the next symbol in the expression is an operand, a tree comprised of a single node labeled with that operand is pushed onto the stack.
If the next symbol in the expression is a binary operator, the top two trees in the stack correspond to its operands. Two trees are popped from the stack and a new tree is created which has the operator as its root and the two trees corresponding to the operands as its subtrees. Then the new tree is pushed onto the stack.

After all the symbols of the expression have been processed in this fashion, the stack will contain a single tree which is the desired expression tree. Figure

illustrates the use of a stack to construct the expression tree from the postfix expression given in Equation

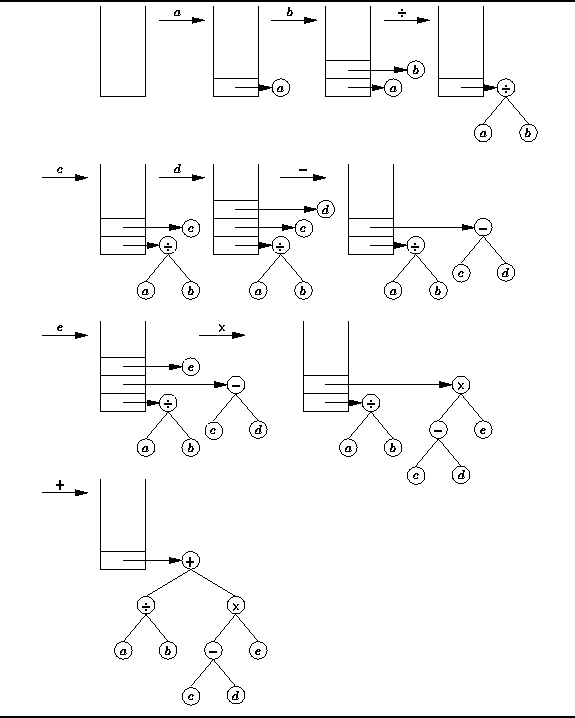
Figure: Postfix to Infix Conversion using a Stack of Trees

Implementation