Exercises

1.   For each tree shown in Figure  show the order in which the nodes are visited during the following tree traversals:
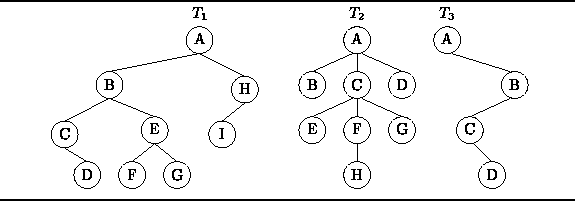
   1. preorder traversal,
   2. inorder traversal (if defined),
   3. postorder traversal, and
   4. breadth-first traversal.

     
   Figure: Sample trees for Exercise 
   

2. Write a visitor that prints the nodes of a general tree in the format of Equation .
3. Derive an expression for the total space needed to represent a tree of n internal nodes using each of the following classes:
   1. GeneralTree defined in Program ,
   2. NaryTree defined in Program , and
   3. BinaryTree defined in Program .
4.   A full node in a binary tree is a node with two non-empty subtrees. Let l be the number of leaf nodes in a binary tree. Show that the number of full nodes is l-1.
5. The generic DepthFirstTraversal routine defined in Program  is a recursive function. Write a non-recursive depth-first traversal routine that has exactly the same effect as the recursive version.
6.   Program  defines a visitor that prints using infix notation the expression represented by an expression tree. Write a visitor that prints the same expression in prefix notation with the following format:

   

7. Repeat Exercise , but this time write a visitor that the expression in postfix notation with the following format:

   

8. The InfixVisitor defined in Program  prints many redundant parentheses because it does not take into consideration the precedence of the operators. Rewrite the visitor so that it prints

   

   rather than

   

9.   Consider postfix expressions involving only binary operators. Show that if such an expression contains n symbols, it always has (n-1)/2 operators and (n+1)/2 operands.
10.   Prove Theorem .
11.   Generalize Theorem  so that it applies to N-ary trees.
12. Consider two binary trees, and and the relation given by

    

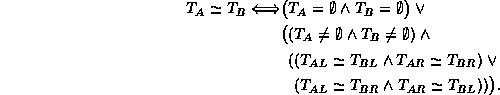
    If , the trees are said to be isomorphic . Devise an algorithm to test whether two binary trees are isomorphic. What is the running time of your algorithm?

Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.