Complete N-ary Trees

The definition for complete binary trees can be easily extended to trees with arbitrary fixed degree as follows:

Definition (Complete N-ary Tree)  A complete N-ary tree   of height , is an N-ary tree with the following properties.

1. If h=0, for all i, .
2. For h>0 there exists a j, such that
   1. is a perfect binary tree of height h-1 for all ;
   2. is a complete binary tree of height h-1; and,
   3. is a perfect binary tree of height h-2 for all i:j<i<N.

Note that while it is expressed in somewhat different terms, the definition of a complete N-ary tree is consistent with the definition of a binary tree for N=2. Figure  shows an example of a complete ternary (N=3) tree.

  
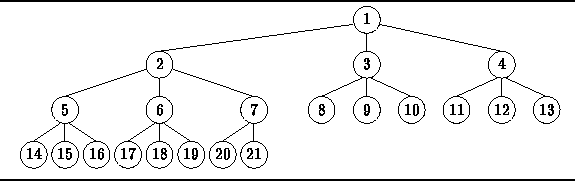
Figure: A Complete Ternary Tree

Informally, a complete tree is a tree in which all the levels are full except for the bottom level and the bottom level is filled from left to right. For example in Figure , the first three levels are full. The fourth level which comprises nodes 14-21 is partially full and has been filled from left to right.

The main advantage of using complete binary trees is that they can be easily stored in an array. Specifically, consider the nodes of a complete tree numbered consecutively in level-order  as they are in Figures  and . There is a simple formula that relates the number of a node with the number of its parent and the numbers of its children.

Consider the case of a complete binary tree. The root node is node 1 and its children are nodes 2 and 3. In general, the children of node i are 2i and 2i+1. Conversely, the parent of node i is . Figure  illustrates this idea by showing how the complete binary tree shown in Figure  is mapped into an array. When using this approach, the pointers are no longer explicitly recorded.

  
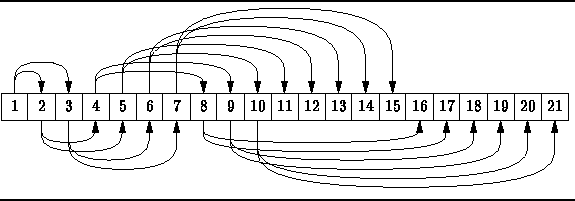
Figure: Array Representation of a Complete Binary Tree

A remarkable characteristic of complete trees is that filling the bottom level from left to right corresponds to adding elements at the end of the array! Thus, a complete tree containing n nodes occupies the first n consecutive array positions.

The array subscript calculations given above can be easily generalized to complete N-ary trees. Assuming that the root occupies position 1 of the array, its N children occupy positions 2, 3, ..., N+1. In general, the children of node i occupy positions

and the parent of node i is found at

Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.