Union by Size

While using collapsing find does mitigate the negative effects of poor trees, a better approach is to avoid creating bad trees in the first place. As shown in Figure , when we join to trees we have a choice--which node should we choose to be the root of the new tree. A simple, but effective choice is to attach the smaller tree under the root of the larger one. In this case, the smaller tree is the one which has fewer nodes. This is the so-called union-by-size  join algorithm. Program  shows how this can be done.

  
Program: PartitionAsForest Class Union-by-Size Join Member Function Definition

The implementation uses the count field of the Container class, from which PartitionTree is derived, to keep track of the number of items contained in the tree. (Since each node contains one item from the universal set, the number of items contained in a tree is equal to the number of nodes in that tree). The algorithm simply selects the tree with the largest number of nodes to become the root of the result and attaches the root of the smaller tree under that of the larger one. Clearly, the running time of the union-by-size version of Join is O(1).

The following theorem shows that when using the union-by-size join operation, the heights of the resulting trees grow logarithmically.

Theorem  Consider an initial partition P of the universe comprised of N sets of size 1. Let S be an element of the partition obtained from P after some sequence of union-by-size join operations, such that |S|=n for some . Let T be the tree representing the set S. The height of tree T satisfies the inequality

extbfProof (By induction).

Base Case Since a tree comprised of a single node has height zero, the theorem clearly holds for n=1.

Inductive Hypothesis Suppose the theorem holds for trees containing n nodes for for some . Consider a union-by-size join operation that produces a tree containing k+1 nodes. Such a tree is obtained by joining a tree having nodes with another tree that has nodes, such that l+m=k+1.

Without loss of generality, suppose . As a result, l is less than or equal to m. Therefore, the union-by-size algorithm will attach under the root of . Let and be the heights of and respectively. The height of the resulting tree is .

According to the inductive hypothesis, the height of is given by

Similarly, the quantity is bounded by

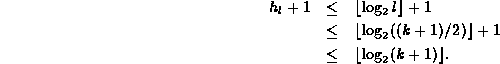
Therefore, the height of the tree containing k+1 nodes is no greater than . By induction on k, the theorem holds for all values of .

Note that Theorem  and its proof does not require that we use the collapsing find algorithm of Section . I.e., the height of a tree containing n nodes is guaranteed to be when the simple find is used. Of course, there is nothing precluding the use of the collapsing find in conjunction with the union-by-size join routine. And doing so only makes things better.

Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.