A great deal of research has gone into the question of finding an appropriate set of parameters to use in Lehmer's algorithm. A good generator has the following characteristics:
The choice of modulus depends on the arithmetic precision used
to implement the algorithm.
A signed 32-bit integer can represent values between ![]() and
and ![]() .
Fortunately, the quantity
.
Fortunately, the quantity ![]() is a prime number!
is a prime number!![]() Therefore, it is an excellent choice for the modulus m.
Therefore, it is an excellent choice for the modulus m.
Because Equation ![]() is slightly simpler than Equation
is slightly simpler than Equation ![]() ,
we choose to implement a multiplicative congruential generator (c=0).
The choice of a suitable multiplier is more difficult.
However, a popular choice is
,
we choose to implement a multiplicative congruential generator (c=0).
The choice of a suitable multiplier is more difficult.
However, a popular choice is ![]() because it satisfies all three criteria given above:
It results in a full period random number generator;
the generated sequence passes a wide variety of statistical tests
for randomness; and
it is possible to compute Equation
because it satisfies all three criteria given above:
It results in a full period random number generator;
the generated sequence passes a wide variety of statistical tests
for randomness; and
it is possible to compute Equation ![]() using 32-bit arithmetic without overflow.
using 32-bit arithmetic without overflow.
The algorithm is derived as follows:
First, let ![]() and
and ![]() .
.![]() In this case,
In this case, ![]() ,
, ![]() and r<q.
and r<q.
Next, we rewrite Equation ![]() as follows:
as follows:
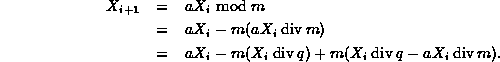
This somewhat complicated formula can be simplified
if we let ![]() :
:
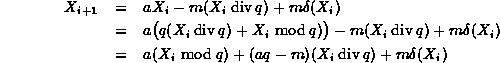
Finally, we make use of the fact that m=aq-r to get
Equation ![]() has several nice properties:
Both
has several nice properties:
Both ![]() and
and ![]() are positive integers between 0 and m-1.
Therefore the difference
are positive integers between 0 and m-1.
Therefore the difference ![]() can be represented using a signed 32-bit integer without overflow.
Finally,
can be represented using a signed 32-bit integer without overflow.
Finally, ![]() is either a zero or a one.
Specifically, it is zero when the sum of the first two terms
in Equation
is either a zero or a one.
Specifically, it is zero when the sum of the first two terms
in Equation ![]() is negative and it is one when the sum is positive.
As a result, it is not necessary to compute
is negative and it is one when the sum is positive.
As a result, it is not necessary to compute ![]() --a simple test suffices to determine whether the third term is 0 or m.
--a simple test suffices to determine whether the third term is 0 or m.