To determine the average running time for the quicksort algorithm,
we shall assume that each element of the sequence has an equal chance
of being selected for the pivot.
Therefore, if i is the number of elements in a sequence of length n
less than the pivot,
then i is uniformly distributed in the interval [0,n-1].
Consequently, the average value of ![]() .
Similarly, the average the value of
.
Similarly, the average the value of
![]() .
To determine the average running time,
we rewrite Equation
.
To determine the average running time,
we rewrite Equation ![]() thus:
thus:
To solve this recurrence we consider the case n>2
and then multiply Equation ![]() by n to get
by n to get
![]()
Since this equation is valid for any n>2, by substituting n-1 for n we can also write
which is valid for n>3.
Subtracting Equation ![]() from Equation
from Equation ![]() gives
gives
![]()
which can be rewritten as
Equation ![]() can be solved by telescoping like this:
can be solved by telescoping like this:
Adding together Equation ![]() through Equation
through Equation ![]() gives
gives
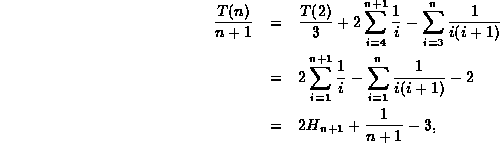
where ![]() is the
is the ![]() harmonic number .
Finally, multiplying through by n+1 gives
harmonic number .
Finally, multiplying through by n+1 gives
![]()
In Section ![]() it is shown that
it is shown that
![]() ,
where
,
where ![]() is called Euler's constant .
Thus, we get that the average running time of quicksort is
is called Euler's constant .
Thus, we get that the average running time of quicksort is
![]()
Table ![]() summarizes the asymptotic running times
for the quicksort routine and compares it to those of bubble sort.
Notice that the best-case and average case running times
for the quicksort algorithm have the same asymptotic bound!
summarizes the asymptotic running times
for the quicksort routine and compares it to those of bubble sort.
Notice that the best-case and average case running times
for the quicksort algorithm have the same asymptotic bound!
| running time | |||
|
algorithm | best case | average case | worst case |
| bubble sort | | | |
| quicksort (random pivot selection) | | | |