The preceding sections present
three ![]() sorting algorithms--quicksort, heapsort, and the two-way merge sort.
But is
sorting algorithms--quicksort, heapsort, and the two-way merge sort.
But is ![]() the best we can do?
In this section we answer the question by showing that
any sorting algorithm that sorts using only binary comparisons
must make
the best we can do?
In this section we answer the question by showing that
any sorting algorithm that sorts using only binary comparisons
must make ![]() such comparisons.
If each binary comparison takes a constant amount of time,
then running time for any such sorting algorithm is also
such comparisons.
If each binary comparison takes a constant amount of time,
then running time for any such sorting algorithm is also ![]() .
.
Consider the problem of sorting the sequence ![]() comprised of three distinct items.
I.e.,
comprised of three distinct items.
I.e., ![]() .
Figure
.
Figure ![]() illustrates a possible sorting algorithm
in the form of a decision tree .
Each node of the decision tree represents one binary comparison.
I.e., in each node of the tree,
exactly two elements of the sequence are compared.
Since there are exactly two possible outcomes for each comparison,
each non-leaf node of the binary tree has degree two.
illustrates a possible sorting algorithm
in the form of a decision tree .
Each node of the decision tree represents one binary comparison.
I.e., in each node of the tree,
exactly two elements of the sequence are compared.
Since there are exactly two possible outcomes for each comparison,
each non-leaf node of the binary tree has degree two.
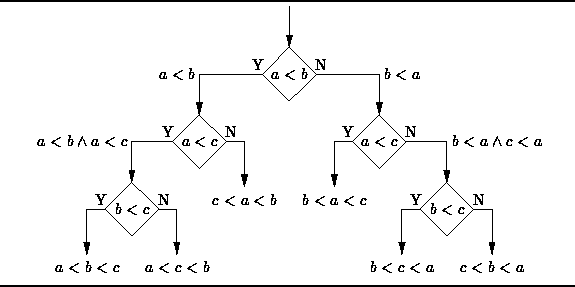
Figure: A Decision Tree for Comparison Sorting
For example, suppose that a<b<c.
Consider how the algorithm shown in Figure ![]() discovers this.
The first comparison compares a and b which reveals that a<b.
The second comparison compares a and c to find that a<c.
At this point it has been determined that a<b and a<c--
the relative order of b and c is not yet known.
Therefore, one more comparison is required to determine that b<c.
Notice that the algorithm shown in Figure
discovers this.
The first comparison compares a and b which reveals that a<b.
The second comparison compares a and c to find that a<c.
At this point it has been determined that a<b and a<c--
the relative order of b and c is not yet known.
Therefore, one more comparison is required to determine that b<c.
Notice that the algorithm shown in Figure ![]() works correctly
in all cases because every possible permutation of the sequence S
appears as a leaf node in the decision tree.
Furthermore, the number of comparisons required in the worst case
is equal to the height of the decision tree!
works correctly
in all cases because every possible permutation of the sequence S
appears as a leaf node in the decision tree.
Furthermore, the number of comparisons required in the worst case
is equal to the height of the decision tree!
Any sorting algorithm that uses only binary comparisons can be represented by a binary decision tree. Furthermore, it is the height of the binary decision tree that determines the worst-case running time of the algorithm. In general, the size and shape of the decision tree is a function of the sorting algorithm and the number of items to be sorted.
Given an input sequence of n items to be sorted,
every binary decision tree that correctly sorts the input sequence
must have at least n! leaves--one for each permutation of the input.
Therefore, it follows directly from Theorem ![]() that the height of the binary decision tree is at least
that the height of the binary decision tree is at least
![]() :
:

Since the height of the decision tree is ![]() ,
the number of comparisons done by
any sorting algorithm that sorts using only binary comparisons
is
,
the number of comparisons done by
any sorting algorithm that sorts using only binary comparisons
is ![]() .
Assuming each comparison can be done in constant time,
the running time of any such sorting algorithm is
.
Assuming each comparison can be done in constant time,
the running time of any such sorting algorithm is ![]() .
.