![]()
For each of the following sorting algorithms, draw a sequence of diagrams that traces the execution of the algorithm as it sorts the sequence S: straight insertion sort, binary insertion sort, bubble sort, quick sort, straight selection sort, heapsort, merge sort, and bucket sort.
![]()
![]()
Prove that bubble sort requires at least p passes where
![]()
- Show that the array is guaranteed to be sorted after n-1 passes.
- What is the running time of this algorithm?
- Show that the array is guaranteed to be sorted after n-1 passes.
- What is the running time of this algorithm?
-
If
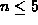 ,
sort S and select directly
the
,
sort S and select directly
the  largest element.
largest element. -
Otherwise n>5:
Partition the sequence S into subsequences of length five.
In general,
there will be
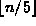 subsequences of length five
and one of length
subsequences of length five
and one of length 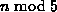 .
. -
Sort by any means each of the subsequences of length five.
(See Exercise
 ).
). -
Form the sequence
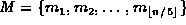 containing the
containing the 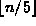 median values
of each of the subsequences of length five.
median values
of each of the subsequences of length five. - Apply the selection procedure recursively to find the median element of M. Let m be the median of the medians.
-
Partition S into three subsequences,
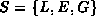 .
such that all the elements in L are less than m,
all the elements in E are equal to m,
and all the elements of G are greater than m.
.
such that all the elements in L are less than m,
all the elements in E are equal to m,
and all the elements of G are greater than m. -
If
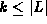 then apply the procedure recursively to select
the
then apply the procedure recursively to select
the  largest element of L;
if
largest element of L;
if 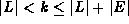 , the result is m;
otherwise apply the procedure recursively to select
the
, the result is m;
otherwise apply the procedure recursively to select
the 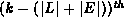 largest element of G.
largest element of G.
- What is the running time of this algorithm?
-
Show that if we use this algorithm to select the pivot
the worst-case running time
of quick sort is
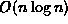 .
.