Single-Source Shortest Path

Data Structures and Algorithms with Object-Oriented Design Patterns in C++

Single-Source Shortest Path

In this section we consider the single-source shortest path problem: Given an edge-weighted graph and a vertex , find the shortest weighted path from to every other vertex in .

Why do we find the shortest path to every other vertex if we are interested only in the shortest path from, say, to ? It turns out that in order to find the shortest path from to , it is necessary to find the shortest path from to every other vertex in G!

Clearly, when we search for the shortest path, we must consider all the vertices in . If a vertex is ignored, say , then we will not consider any of the paths from to that pass through . But if we fail to consider all the paths from to , we cannot be assured of finding the shortest one.

Furthermore, suppose the shortest path from to passes through some intermediate node . I.e., the shortest path is of the form It must be the case that the portion of P between to is also the shortest path from to . Suppose it is not. Then there exists another shorter path from to . But then, P would not be the shortest path from to , because we could obtain a shorter one by replacing the portion of P between and by the shorter path.

Consider the directed graph shown in Figure . The shortest weighted path between vertices b and f is the path which has the weighted path length nine. On the other hand, the shortest unweighted path is from b to f is the path of length three, .

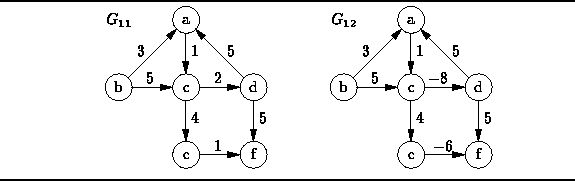
Figure: Two Edge-Weighted Directed Graphs

As long as all the edge weights are non-negative (as is the case for ), the shortest-path problem is well defined. Unfortunately, things get a little tricky in the presence of negative edge weights.

For example, consider the graph shown in Figure . Suppose we are looking for the shortest path from d to f. Exactly two edges emanate from vertex d, both with the same edge weight of five. If the graph contained only positive edge weights, there could be no shorter path than the direct path .

However, in a graph that contains negative weights, a long path gets ``shorter'' when we add edges with negative weights to it. E.g., the path has a total weighted path length of four, even though the first edge, (d,a), has the weight five.

But negative weights are even more insidious than this: For example, the path , which also joins vertex d to f, has a weighted path length of two but the path has length zero. I.e., as the number of edges in the path increases, the weighted path length decreases! The problem in this case is the existence of the cycle the weighted path length of which is less than zero. Such a cycle is sometimes called a negative cost cycle .

Clearly, the shortest-path problem is not defined for graphs that contain negative cost cycles. However, negative edges are not intrinsically bad. Solutions to the problem do exist for graphs that contain both positive and negative edge weights, as long as there are no negative cost cycles. Nevertheless, the problem is greatly simplified when all edges carry non-negative weights.