In this section we consider undirected graphs and their subgraphs.
A subgraph of a graph ![]() is any graph
is any graph ![]() such that
such that ![]() and
and ![]() .
In particular, we consider connected undirected graphs
and their minimal subgraphs .
The minimal subgraph of a connected graph is called a spanning tree:
.
In particular, we consider connected undirected graphs
and their minimal subgraphs .
The minimal subgraph of a connected graph is called a spanning tree:
Definition (Spanning Tree) Consider a connected, undirected graph. A spanning tree of G is a subgraph of G, say
, with the following properties:
.
- T is connected.
- T is acyclic.
Figure ![]() shows an undirected graph,
shows an undirected graph, ![]() ,
together with three of its spanning trees.
A spanning tree is called a tree
because every acyclic undirected graph
can be viewed as a general, unordered tree.
Because the edges are undirected,
any vertex may be chosen to serve as the root of the tree.
For example, the spanning tree of
,
together with three of its spanning trees.
A spanning tree is called a tree
because every acyclic undirected graph
can be viewed as a general, unordered tree.
Because the edges are undirected,
any vertex may be chosen to serve as the root of the tree.
For example, the spanning tree of ![]() given in Figure
given in Figure ![]() (c)
can be viewed as the general, unordered tree
(c)
can be viewed as the general, unordered tree
![]()
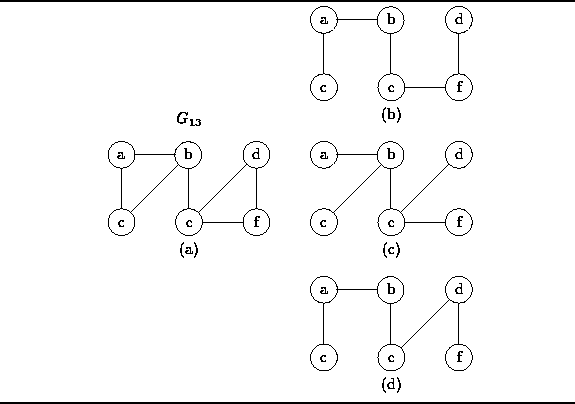
Figure: An Undirected Graph and Three Spanning Trees
According to Definition ![]() ,
a spanning tree is connected.
Therefore, as long as the tree contains more than one vertex,
there can be no vertex with degree zero.
Furthermore, the following theorem guarantees that there is always
at least one vertex with degree one:
,
a spanning tree is connected.
Therefore, as long as the tree contains more than one vertex,
there can be no vertex with degree zero.
Furthermore, the following theorem guarantees that there is always
at least one vertex with degree one:
Theorem Consider a connected, undirected graph, where
. Let
be a spanning tree of G. The spanning tree T contains at least one vertex of degree one.
extbfProof (By contradiction). Assume that there is no vertex in T of degree one. I.e., all the vertices in T have degree two or greater. Then by following edges into and out of vertices we can construct a path that is cyclic. But a spanning tree is acyclic--a contradiction. Therefore, a spanning tree always contains at least one vertex of degree one.
According to Definition ![]() ,
the edge set of a spanning tree
is a subset of the edges in the spanned graph.
How many edges must a spanning tree have?
The following theorem answers the question:
,
the edge set of a spanning tree
is a subset of the edges in the spanned graph.
How many edges must a spanning tree have?
The following theorem answers the question:
Theorem Consider a connected, undirected graph. Let
be a spanning tree of G. The number of edges in the spanning tree is given by
extbfProof (By induction).
We can prove Theorem ![]() by induction on
by induction on ![]() ,
the number of vertices in the graph.
,
the number of vertices in the graph.
Base Case
Consider a graph that contains only one node, i.e., ![]() .
Clearly, the spanning tree for such a graph contains no edges.
Since
.
Clearly, the spanning tree for such a graph contains no edges.
Since ![]() ,
the theorem is valid.
,
the theorem is valid.
Inductive Hypothesis
Assume that the number of edges in a spanning tree for a graph
with ![]() has been shown to be
has been shown to be ![]() for
for ![]() .
.
Consider a graph ![]() with k+1 vertices
and its spanning tree
with k+1 vertices
and its spanning tree ![]() .
According to Theorem
.
According to Theorem ![]() ,
,
![]() contains at least one vertex of degree one.
Let
contains at least one vertex of degree one.
Let ![]() be one such vertex
and
be one such vertex
and ![]() be the one edge emanating from v in
be the one edge emanating from v in ![]() .
.
Let ![]() be the graph of k nodes obtained by removing v
and its emanating edge from the graph
be the graph of k nodes obtained by removing v
and its emanating edge from the graph ![]() .
I.e.,
.
I.e., ![]() .
.
Since ![]() is connected, so too is
is connected, so too is ![]() .
Similarly, since
.
Similarly, since ![]() is acyclic, so too is
is acyclic, so too is ![]() .
Therefore
.
Therefore ![]() is a spanning tree with k vertices.
By the inductive hypothesis
is a spanning tree with k vertices.
By the inductive hypothesis ![]() has k-1 edges.
Thus,
has k-1 edges.
Thus, ![]() as k edges.
as k edges.
Therefore, by induction on k,
the spanning tree for a graph with ![]() vertices
contains
vertices
contains ![]() edges.
edges.