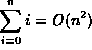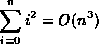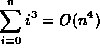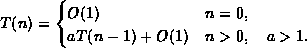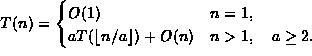| f(n) | g(n) |
| 10n | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
![]()
for ![]() .
.
- The worst case running time for e(n,m,k) is O(1) and it returns a value between 1 and (n+m+k).
- The worst case running time for f(n,m,k) is O(n+m).
- The worst case running time for g(n,m,k) is O(m+k).
- The worst case running time for h(n,m,k) is O(n+k).
-
f (n, 10, 0); g (n, m, k); h (n, m, 1000000);
-
for (unsigned int i = 0; i < n; ++i) f (n, m, k); -
for (unsigned int i = 0; i < e (n, 10, 100); ++i) f (n, 10, 0); -
for (unsigned int i = 0; i < e (n, m, k); ++i) f (n, 10, 0); -
for (unsigned int i = 0; i < n; ++i) for (unsigned int j = i; j < n; ++j) f (n, m, k);
unsigned int f (unsigned int n)
{
unsigned int sum = 0;
for (unsigned int i = 1; i <= n; ++i)
sum = sum + i;
return sum;
}unsigned int g (unsigned int n)
{
unsigned int sum = 0;
for (unsigned int i = 1; i <= n; ++i)
sum = sum + i + f (n);
return sum;
}unsigned int h (unsigned int n)
{ return f (n) + g (n); }