|
Data Structures and Algorithms
with Object-Oriented Design Patterns in C# |
| f(n) | g(n) |
| 10n | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
![]()
for ![]() .
.
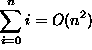
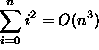
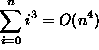
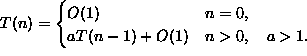
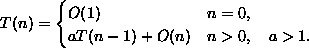
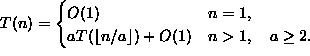
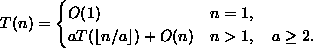
F(n, 10, 0); G(n, m, k); H(n, m, 1000000);
for (int i = 0; i < n; ++i)
F(n, m, k);for (int i = 0; i < E(n, 10, 100); ++i)
F(n, 10, 0);for (int i = 0; i < E(n, m, k); ++i)
F(n, 10, 0);for (int i = 0; i < n; ++i)
for (int j = i; j < n; ++j)
F(n, m, k);
public class Example
{
public static int F(int n)
{
int sum = 0;
for (int i = 1; i <= n; ++i)
sum = sum + i;
return sum;
}
// ...
}public class Example
{
// ...
public static int G(int n)
{
int sum = 0;
for (int i = 1; i <= n; ++i)
sum = sum + i + F(i);
return sum;
}
}public class Example
{
// ...
public int H(int n)
{ return F(n) + G(n); }
}