Array Subscript Calculations

Data Structures and Algorithms with Object-Oriented Design Patterns in C#

Array Subscript Calculations

The memory of a computer is essentially a one-dimensional array--the memory address is the array subscript. Therefore, a natural way to implement a multi-dimensional array is to store its elements in a one-dimensional array. In order to do this, we need a mapping from the n subscript expressions used to access an element of the multi-dimensional array to the one subscript expression used to access the one-dimensional array. For example, suppose we wish to represent a array of of ints, a, using a one-dimensional array like this:

int[] b = new int[6];

Then we need to determine which element of b, say b[k], will be accessed given a reference of the form a[i,j]. That is, we need the mapping f such that

The mapping function determines the way in which the elements of the array are stored in memory. The most common way to represent an array is in row-major order , also known as lexicographic order . For example, consider the two-dimensional array. The row-major layout of this array is shown in Figure .

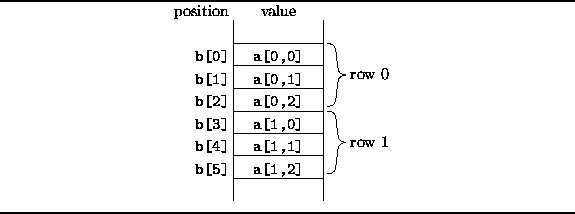
Figure: Row-major order layout of a 2D array.

In row-major layout, it is the right-most subscript expression (the column index) that increases the fastest. As a result, the elements of the rows of the matrix end up stored in contiguous memory locations. In Figure , the first element of the first row is at position b[0]. The first element of the second row is at position b[3], since there are 3 elements in each row.

We can now generalize this to an arbitrary n-dimensional array. Suppose we have an n-D array a with dimensions

Then, the position of the element a[ , , , ] is given by

where

The running time required to calculate the position appears to be since the position is the sum of n terms and for each term we need to compute , which requires O(n) multiplications in the worst case. However, the factors are determined solely from the dimensions of the array. Therefore, we need only compute the factors once. Assuming that the factors have been precomputed, the position calculation can be done in O(n) time using the following algorithm:

int offset = 0;
for (int j = 1; j <= n; ++j)
    offset += 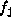  *  ;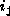