The final variation of hashing to be considered here is called the Fibonacci hashing method . In fact, Fibonacci hashing is exactly the multiplication hashing method discussed in the preceding section using a very special value for a. The value we choose is closely related to the number called the golden ratio.
The golden ratio is defined as follows:
Given two positive numbers x and y,
the ratio ![]() is the golden ratio if
the ratio of x to y is the same as that of x+y to x.
The value of the golden ratio can be determined as follows:
is the golden ratio if
the ratio of x to y is the same as that of x+y to x.
The value of the golden ratio can be determined as follows:
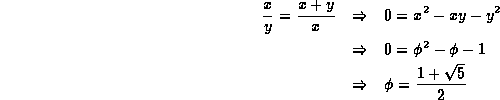
There is an intimate relationship between the golden ratio and the
Fibonacci numbers .
In Section ![]() it was shown that the
it was shown that the ![]() Fibonacci
number is given by
Fibonacci
number is given by
![]()
where ![]() and
and ![]() !
!
The Fibonacci hashing method
is essentially the multiplication hashing method
in which the constant a
is chosen as the integer that is relatively prime to W
which is closest to ![]() .
The following table gives suitable values of a
for various word sizes.
.
The following table gives suitable values of a
for various word sizes.
| W | |
| | 40503 |
|
| 2654435769 |
|
| 11400714819323198485 |
Why is ![]() special?
It has to do with what happens to consecutive keys
when they are hashed using the multiplicative method.
As shown in Figure
special?
It has to do with what happens to consecutive keys
when they are hashed using the multiplicative method.
As shown in Figure ![]() ,
consecutive keys are spread out quite nicely.
In fact, when we use
,
consecutive keys are spread out quite nicely.
In fact, when we use ![]() to hash consecutive keys,
the hash value for each subsequent key falls
in between the two widest spaced hash values already computed.
Furthermore, it is a property of the golden ratio,
to hash consecutive keys,
the hash value for each subsequent key falls
in between the two widest spaced hash values already computed.
Furthermore, it is a property of the golden ratio, ![]() ,
that each subsequent hash value divides the interval into which it falls
according to the golden ratio!
,
that each subsequent hash value divides the interval into which it falls
according to the golden ratio!