When dealing with directed graphs, we define two kinds of connectedness, strong and weak. Strong connectedness of a directed graph is defined as follows:
Definition (Strong Connectedness of a Directed Graph) A directed graphis strongly connected if there is a path in G between every pair of vertices in
.
For example, Figure ![]() shows the directed graph
shows the directed graph
![]() given by
given by
![]()
Notice that the graph ![]() is not connected!
For example, there is no path from any of the vertices in
is not connected!
For example, there is no path from any of the vertices in ![]() to any of the vertices in
to any of the vertices in ![]() .
Nevertheless, the graph ``looks'' connected
in the sense that it is not made of up of separate parts
in the way that the graph
.
Nevertheless, the graph ``looks'' connected
in the sense that it is not made of up of separate parts
in the way that the graph ![]() in Figure
in Figure ![]() is.
is.
This idea of ``looking'' connected
is what weak connectedness represents.
To define weak connectedness we need to introduce first
the notion of the undirected graph that underlies a directed graph:
Consider a directed graph ![]() .
The underlying undirected graph is the graph
.
The underlying undirected graph is the graph
![]() where
where
![]() represents the set of undirected edges that is obtained
by removing the arrowheads from the directed edges in G:
represents the set of undirected edges that is obtained
by removing the arrowheads from the directed edges in G:
![]()
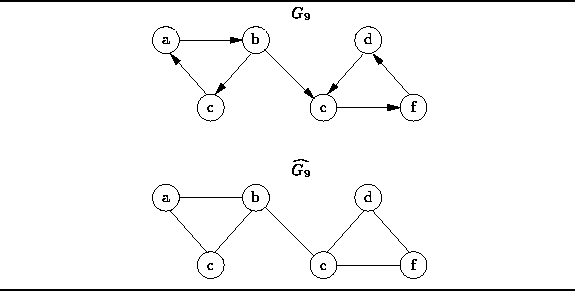
Figure: An weakly connected directed graph and the underlying undirected graph.
Weak connectedness of a directed graph is defined with respect to its underlying, undirected graph:
Definition (Weak Connectedness of a Directed Graph) A directed graphis weakly connected if the underlying undirected graph
is connected.
For example,
since the undirected graph ![]() in Figure
in Figure ![]() is connected,
the directed graph
is connected,
the directed graph ![]() is weakly connected.
Consider what happens when we remove the edge (b,e)
from the directed graph
is weakly connected.
Consider what happens when we remove the edge (b,e)
from the directed graph ![]() .
The underlying undirected graph that we get is
.
The underlying undirected graph that we get is ![]() in Figure
in Figure ![]() .
Therefore,
when we remove edge (b,e) from
.
Therefore,
when we remove edge (b,e) from ![]() ,
the graph that remains is neither strongly connected nor weakly connected.
,
the graph that remains is neither strongly connected nor weakly connected.