
In this section we present some simple rules for determining a big-oh upper bound on the running time of the basic compound statements in a Java program.
Rule ![]() follows directly from Theorem
follows directly from Theorem ![]() .
The total running time of a sequence of statements is equal to the
sum of the running times of the individual statements.
By Theorem
.
The total running time of a sequence of statements is equal to the
sum of the running times of the individual statements.
By Theorem ![]() ,
when computing the sum of a series of functions
it is the largest one (the
,
when computing the sum of a series of functions
it is the largest one (the ![]() ) that determines the bound.
) that determines the bound.
Rule ![]() appears somewhat complicated due to the semantics
of the Java for statement.
However, it follows directly from Theorem
appears somewhat complicated due to the semantics
of the Java for statement.
However, it follows directly from Theorem ![]() .
Consider the following simple counted do loop .
.
Consider the following simple counted do loop .
for (int i = 0; i < n; ++i)
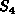 ;
;
Here int i = 0, so its running time is constant ( i < n, so its running time is constant ( ++i, so its running time is constant (
If we don't know the exact number of iterations executed, I(n),
we can still use Rule ![]() provided we have an upper bound,
I(n)=O(f(n)), on the number of iterations executed.
In this case, the running time is
provided we have an upper bound,
I(n)=O(f(n)), on the number of iterations executed.
In this case, the running time is
![]() .
.
Rule ![]() follows directly from the observation
that the total running time for an if-then-else statement
will never exceed the sum of the running time of the conditional test,
follows directly from the observation
that the total running time for an if-then-else statement
will never exceed the sum of the running time of the conditional test,
![]() , plus the larger of the running times of the then part,
, plus the larger of the running times of the then part, ![]() ,
and the else part,
,
and the else part, ![]() .
.