

![[previous]](left.gif)
![[Table of Contents]](toc.gif)
![[next]](../right.gif)
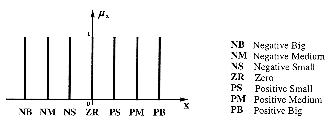
Nonlinear characteristics are realized in fuzzy logic by partitioning the rule space, bu weighting the rules, and by the nonlinear membership function. Rule-based systems compute their output by combining results from different parts of the partition, each part being governed by separate rules. In fuzzy reasoning, the boundaries of these parts overlap, and the local results are combined by weighting them appropriately. That is why the output in a fuzzy system is a smooth, nonlinear function.
In decision-making systems, the target of modeling is not a control
surface but the person whose decision-making is to be emulated. This kind
of modeling is outside the realm of conventional control theory. Fuzzy
reasoning can tackle this easily since it can handle qualitative knowledge
(e.g. linguistic terms like “big” and “fast”, and rules of thumb) directly.
In most applications to consumer products, fuzzy systems do not directly
control the actuators, but determine the parameters to be used for control.
For example, they may determine washing time in washing machines, or if
it is the hand or the image that is shaking in a camcorder, or they compute
which object is supposed to be the focus in an auto-focus system, or they
determine the contrast optimal for watching television.
A fuzzy system encodes knowledge at two levels: knowledge which incorporates
fuzzy heuristics, and the knowledge that defines the terms being used in
the former level. Due to this separation of meaning, it is possible to
directly encode linguistic rules and heuristics. This reduces the development
time, since the expert’s knowledge can be directly built in.
Although the developed fuzzy system may have complex input-output characteristics, as long as the mapping is static during the operation of the device, the mapping can be discretized and implemented as a memory lookup on simple hardware. This further reduces the costs involved in incorporating the knowledge into the device.
Mamdani introduced the fuzzification/inference/defuzzification scheme and used an inference strategy that is generally mentioned as the max-min method. This inference type is a way of linking input linguistic variables to output ones in accordance with the generalized modus ponens, using only the MIN and MAX functions (as T-norm and S-norm (or T-conorm) respectively). It allows to achieve approximate reasoning (or interpolative inference).
Let consider a set of inference rules in the guise of a fuzzy associative memory (FAM) represented in an inference matrix or table, and some fuzzy sets and respective membership functions that have been attributed to each variables (fuzzification). Figure 2.1 represents the case where 2 rules are activated involving 2 input variables (x & y) and one output variable (r). Let assume x be a measure of x(t) at time t, and y a measure of y(t) at the same time. Let now consider the fuzzy sets A1, A2, B0 and B1 which respective membership functions µA1(x), µA2(x), µB0(y) and µB1(y) take positive values for x and y. Affected inference rules are for example as follow:
if (x = A1 AND y = B0) then r = C0 else if (x = A2 AND y = B1) then r = C1They also can be expressed as follow:
![[Zoom]](zoom.gif)
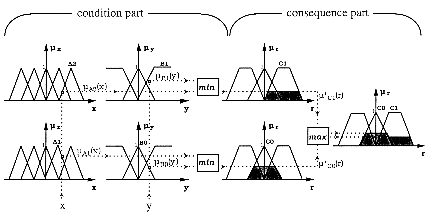
The max-min method finally requires a defuzzification stage which is generally performed using the centre of gravity method. It will give for the above example the real value r, using the membership function resulting from the max-min method:
The max-prod method for example is similar to the max-min method, except that all implications in the rules (then operations) are realised by a product instead of a minimisation. The truth values of the rule conditions are used to multiply uniformly the corresponding output sets instead of clipping them at a certain level. This allow to keep the information that consist in the shape of these sets, and that is partly lost with the max-min method. The product is moreover simpler and faster to execute than the minimum operator in software implementations and allows some simplifications in numerical realizations of inferences (since it can deal with analytic expressions instead of comparing each couple of stored points).
Another common method is the sum-prod method that uses the arithmetical mean and the product to realise respectively all the OR & AND operators. Unlike the MAX operator which select only the maximums values, the sum takes into account all involved sets and conserves part of the information that contain their shapes.
These different methods are described and compared in [Büh94]. From this analysis emerges the fact that they lead to very similar input/output characteristics in the case of a single input variable, when used with triangular or trapezoid output sets. With several input variables, the max-min method produces non-linear characteristics with strong discontinuities, while the sum-prod method produces non-linear characteristics with smoother discontinuities. Nevertheless the choice of a specific method is mainly influenced by the way to implement it. This suggests the choice of the max-min method for hardware implementations, because the MAX and MIN operators are then the easiest to implement. These two operators are moreover the most robust to realize T- and S-norm according to the authors of [Ngu93]. Since they are the most reliable when membership grades have imprecise and noisy values they are well appropriate to fuzzy hardware with questionable accuracy. The max-min method is finally well suitable for fuzzy rule-based systems when there is no precise model. It generally leads in a simple way to consistent rules as it can be noticed in practical applications.
The choice of an inference method has nevertheless a great importance for one-rule inferences, to select for example one among several candidates or to choose an optimal solution (this case is frequent especially in non-technical fields). The operators are then to be chosen with care because they influence directly the criterion of evaluation and consequently the final decision.
Finally, one important aspect of Mamdani's method is that it is essentially heuristic and it can sometimes be very difficult to express an operator's or engineer's knowledge in terms of fuzzy sets and implications. Moreover such a knowledge is often incomplete and episodic rather than systematic. There is in fact no specific methodology for clearly deriving and analysing a rule base of a fuzzy inference system (there is consequently no exhaustive choice of optimal rule and set numbers, shapes, operators,...). Since their principle seems to be rather simple, fuzzy system includes a lot of parameters and can lead then to a great deal of different and complicated characteristics. Some problems may occur when the rules have to describe a process that is too complex or to deal with a high number of variables. It can be then very difficult to define a sufficient set of coherent rules, and the danger of having not enough or conflicting rules occurs. There are several methods used to optimise inference rules and fuzzy sets, that are more or less perfected and sometimes quite complicated (typical ones are gradient method, least squares method, simulated annealing, neural-networks, etc.). They give rise to adaptive fuzzy systems which parameters are suited to the conditions of a specific application. The high parametrical level of fuzzy systems makes automatic adaptation solutions rather difficult.
Mamdani-type control is simpler than most of standard ones and requires much shorter development cycle when linguistic rules can be easily expressed (because there is no need to develop, analyse and implement a mathematical model). It is even in several cases as or more efficient, especially when no precise model exists, for example when a process to control is governed by non-linear laws or includes bad-known parameters or disturbances. When the mathematical model contains some non-linear terms, they are linearized and simplified under the assumption of small error signals, whereas a non-linear fuzzy method often allows to control bigger ranges of error.
The non-linearity of Mamdani-type control can moreover have a favourable influence on transitory phenomenon. Consequently it can sometimes supplant classic control to provide fast responses. When increasing the response speed of conventional controllers the overshoot is also increasing (in position control for example). Generally fuzzy controllers with highly non-linear characteristics gives lower overshoot before setting time than conventional PID control, but small oscillations often remain after settlement. This oscillatory behaviour can become very difficult to restrain and fuzzy controllers are sometimes combined with conventional ones (in cascade configuration for example) to exploit the advantages of both. However fuzzy controllers can also have perfectly linear characteristics and replace standard comtrollers, which can sometimes be useful to provide some features of fuzzy controllers.
Fuzzy control is attractive in some cases where parameters are varying with time and easily expressed into linguistic terms. It is indeed easier to reassign one or several fuzzy rules rather than to calculate the mathematical equations of a new model necessary to adapt classic controllers. However these last ones have a smaller number of parameters to adjust, and these parameters can for example be issued from a fuzzy system which regulates them according to the features fluctuations of a controlled process.
![[Zoom]](zoom.gif)
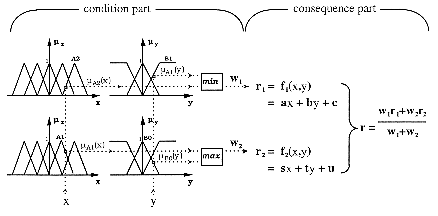
Control rules are deriving in the following way:
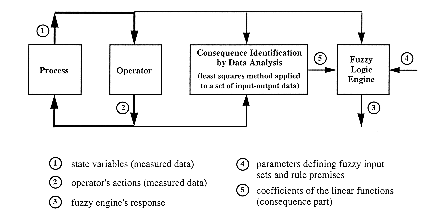
Let the antecedent part results from a specific fuzzification achieved according to human operator's or engineer's knowledge. That means some fuzzy sets and some logical functions making up premises are defined. The input space has been thus divided into a certain number of fuzzy subsets, i.e. a certain number of fuzzy rules. Then the setting-up of the consequence part of the rules requires a certain amount of numerical data (corresponding to input and output variables) coming from the operation which has to be modelled (fig. 2.3). The coefficients of each linear function are identified from the analysis of these data in order to minimized the difference between outputs of an original system and the ones of a model (fuzzy engine). This optimisation is achieved by the analysis of a weighted linear regression using a certain amount of input data (the weights are calculated as the truth degrees of the fuzzy conditions).
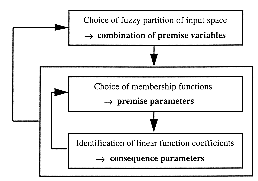
Finally the system identification is function of the consequence parameters (coefficients in the linear functions) as well as the premise parameters (input sets) and the fuzzy partition of the input space. The identification of this last has no solution since it is a combinatorial problem and is generally issued from an heuristic search. An iterative algorithm for parameters and structure identification can be used efficiently (fig. 2.4) [Sug85],[Tak85]. The resulting fuzzy model gives generally much better results than a statistical model [Tak83].
![[Zoom]](zoom.gif)
![[Zoom]](zoom.gif)
Takagi-Sugeno'rules implementation is simplified because there is no need of a defuzzification stage. Output values are simply calculated from input ones, using a set of weighted linear functions. One needs however to be able to collect a certain amount of data (sometimes during a rather long period for time-varying processes) and then to find good coefficients with the least squares method. Measurements and data analysis often require a great deal of time, and it is furthermore not always possible to find satisfying coefficients. Takagi-Sugeno' method becomes actually difficult or even impossible to apply when a control has strongly non-linear characteristics (for example when there is a large hysteresis loop) or which is moreover changing with time.
Some method as the simulated annealing for example could be used to reduce the iterative sequence of tests achieving the coefficients and structure identification. The approximation of measured characteristic or of a calculated linear regression could also be efficiently achieved by using a neural network. The structure identification would then result from a supervised learning phase instead of a long and unwieldy iterative research.
![[Zoom]](zoom.gif)
The use of singletons has no bad consequence on the output variable domain which can be the same as with triangular or trapezoid output sets when using the centre of gravity method. The nonlinearity of a controller characteristic can be modulated by the distribution of these sets (but not more by their shapes). The difficulty to describe some processes can however be then increased in comparison with the use of more complex sets in Mamdani'method or the use of linear functions in Takagi-Sugeno'method. For the latter, the restriction to constant functions in the consequence part doesn't allow any more to describe complicated relationships between input and output variables in a rather simple format. This method leads then sometimes to a worse minimisation of the output error between a real process and a fuzzy model, and structure identification (fuzzy partition of the input space) has to be much more improved to obtain satisfactory results in complicated cases.
The design of fuzzy dedicated integrated circuits is however of great interest, because of the increasing number of fuzzy applications requiring highly parallel and high-speed fuzzy processing. They attempt to give a concrete expression to the idea of "fuzzy computers" (sometimes called computers of the sixth generation), which deal with analog values or some digital representation of them. Fuzzy processors are designed in a way to optimise fuzzy logic functions (cf.§3.2) as regards their implementation size and execution speed. Since practical systems often require a great number of rule evaluations per second, a huge amount of real- time data processing is necessary and the speed of fuzzy circuits is of prime importance. Their architectures are generally suited to the structure of approximate reasoning and decision- making algorithms and generally include three distinct parts, proceeding fuzzification, inference and defuzzification respectively. Fuzzy controllers are thus made on one hand of a knowledge base, which contains rules and membership functions outlines, as other configuration parameters of the system. On the other hand stands an inference mechanism (based on interpolative reasoning) interfacing a real process in a feedback loop configuration.
![[Zoom]](zoom.gif)
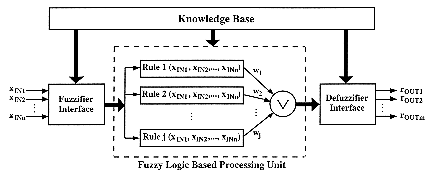
The structure of fuzzy dedicated circuits is characterized by the number and shape range of input and output variables, the number of rules they can evaluate simultaneously, the type(s) of inference(s) (size of premises, operators, consequences,...), the type(s) of defuzzification method(s), and so on. Their performance is evaluated according to their processing speed (that is the number of fuzzy logic inferences per second (FLIPS)), as to their precision (error and noise generation in analog circuits and number of bit representing fuzzy values in digital ones). Fast response is required for non-linear functions as MIN and MAX which output signals can be subject to sudden discontinuities. These functions are however piecewise linear and accuracy is also quite important.
Fuzzy chips are mainly used in expert systems as well as in control and command field to achieve real-time performance. They are however less efficient for applications that deal with a large amount of data, because of the limited I/O. It can thus be interesting to design several compatible circuits, identical or different. They can be for example dedicated to inference rules and defuzzification respectively. In this manner it is possible to connect them together in several different ways, using some of them for example to proceed parallel fuzzifications and inferences, and connecting them to a defuzzification circuit [Hir93]. With a large number of input variables it may be useful to split up the control system into several cascaded or superposed units, which aims at simplifying the inference engine [Büh94].
Fuzzy software is useful when an application can be modelled to simulate and calculate in advance a multidimensional response characteristic. They give the different parameters relative to an optimal characteristic in order to design or program a fuzzy dedicated circuit. Some of these parameters (fuzzy sets and inference rules) have just to be adjusted then in the real implementation. In some simple cases, the numeric response characteristic can be stored as a reference rule table in a multidimensional associative memory, and provides then response values for real-time proceeding without any more inference calculations. The stored values are provided by fuzzy software (when a model exist), by the measure of an operator's action or by an adaptive system with a retroactive learning scheme (which comes close to the principle of fuzzy dedicated neural networks)[Chan93].
When no model exists, a fuzzy processor has to be programmable because its parameters are established by iterative testing on the real implementation, not by simulation. This process requires a lot of tests and is time consuming, and may furthermore not necessarily reach an optimal solution. Since no simulation of the system's dynamic behaviour are achieved, the danger of unstable working states occurs in control applications. The configuration flexibility of integrated fuzzy system requires a great storage capacity (digital circuits) or tunable components (analog circuits) to deal with variable numbers and shapes of membership functions as variable numbers and sizes of rules. Since the shape of the membership functions is generally less important than their degree of overlap the horizontal position of sets should always be tunable, but often complicated shapes are not essential.
![[Zoom]](zoom.gif)
Conventional operators as algebraic sum (+), algebraic difference (-),
algebraic product (.) are commonly used in fuzzy reasoning systems. The
first nine fuzzy operators are the more commonly used in hardware system
design to implement fuzzy information processing. They have moreover the
particularity that they all can be expressed by the only bounded difference
(![]() ) and algebraic sum
(+) functions [Yam86],[Zhij90],[Sas90]. There has been several approaches
using these two functions to design fuzzy units, which provides attractive
perspectives for CAD automation and semicustom circuits. Other operators
also allows to express any fuzzy formulae when combined together, as for
example the bounded sum (
) and algebraic sum
(+) functions [Yam86],[Zhij90],[Sas90]. There has been several approaches
using these two functions to design fuzzy units, which provides attractive
perspectives for CAD automation and semicustom circuits. Other operators
also allows to express any fuzzy formulae when combined together, as for
example the bounded sum ( ![]() )
and the bounded product (
)
and the bounded product ( ![]() )
[Lem94]. These ones are associative and commutative, but are not distributive
to each other. The non-distributiveness of bounded operators leads to long
and complicated manipulations when used to solve fuzzy formulae, and it
is quite not obvious to substite or eliminate some terms. Fuzzy formulae
are unfortunately not able to be reduced as much and as simply than boolean
formulae.
)
[Lem94]. These ones are associative and commutative, but are not distributive
to each other. The non-distributiveness of bounded operators leads to long
and complicated manipulations when used to solve fuzzy formulae, and it
is quite not obvious to substite or eliminate some terms. Fuzzy formulae
are unfortunately not able to be reduced as much and as simply than boolean
formulae.
Some other fuzzy operators as symmetric difference (![]() ),
drastic difference (
),
drastic difference (![]() ),
drastic sum (
),
drastic sum ( ![]() )
or drastic product (
)
or drastic product (![]() )
are sometimes to resolve some fuzzy equations.
)
are sometimes to resolve some fuzzy equations.
![[Table of Contents]](toc.gif)
![[Top of Document]](top.gif)
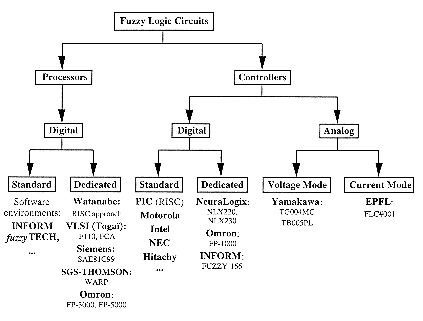
The first hardware approaches of implementing fuzzy logic inference engine were the digital circuits designed by Togai and Watanabe [Tog86],[Tog87],[Wat90]. ASIC's implementing specific architectures and specialized instructions (MIN & MAX) exhibits much enhanced processing speed relatively to regular microprocessors.
architectures: Fuzzy microcontroller (embedded systems with A/D & D/A converters, Fuzzy arithmetic logic unit (FALU) and specific memories, ...) versus fuzzy coprocessor; coprocessor. Sequential processing -> enhance speed by parallel, pipeline [Nak93], systolic, RISC, SIMD architectures
fuzzification strategy, defuzzification strategy
For applications where a restricted number of pins of a chip can be inappropriate (such as fuzzy databases (= ambiguous data or fuzzy relations between crisp data)), a fuzzy coprocessor is used rather than a stand-alone chip. When other conventionnal digital processing are required (flexible system)
The input are furthermore sampled at the frequency of digital circuits. Sampling effects: non-continuous (or pseudo-continuous) control [Büh94] § 7.3
NeuraLogix' controllers
INFORM's FUZZY-166 Processor
High prices must be reduced to make these processors more attractive.
Some less common hardware implementations such as pulse-width-modulation [Ung93] or sperconducting processor have also been implemented, and are not exclude from future developments according to technological evolution.
Analog controllers can achieve fuzzy real-time reasoning with a large amount of fuzzy implications, especially when no high-level accuracy is required. They are well suited to deal with vague and imprecise models, like for example some tasks that interface human senses (eye, tactile nerves, ear,...) or replace human reasoning (pattern recognition, reflex processes,...). Accuracy of fuzzy systems is actually not always so important since there is no thorough mathematical background usable to define precise and exhaustive fuzzy methods. Imprecise but adjustable analog devices are consequently suitable for a great number of cases (tunable membership functions are thus needed to optimize the performance). They are nevertheless much less flexible and adaptable than digital ones that are programmable, and they must be designed according to the structure of a specific application. A basic programmability is afforded when some analog external parameters can be adjusted or when some binary inputs allow the control of internal switches.
The choice of common fuzzy operators (§3.2) is not exhaustive, and other methods could just as well be implemented since there is no mathematical proof than some of them are really optimal. Thus some other operators can be chosen instead of the common MIN and MAX ones, in order to be efficiently performed with analog circuits. Some dense, fast and accurate hardware operators can give very good practical results, even if they are theoretically not optimal. A novel way of evaluating the condition part of fuzzy rules has thus been introduced in [Land93]. The degree of membership of an input vector to some fuzzy subspace is defined using a measure of distance between this vector and some central point in the subspace. MIN and MAX operators are not implemented any more and very dense and high-speed analog hardware may be realised (in current-mode).
Analog signals are represented either by voltages (voltage-mode, §5.2) or by currents (current-mode, §5.4). Stable and low-noise analog technologies (n-well CMOS, BiCMOS) must be used in order to design analog circuits having sufficient accuracy with wide frequency range. Reliable CAD tools for automatic design as fast verification and simulation tools are required for effective design.
![[Zoom]](zoom.gif)
![[Zoom]](zoom.gif)
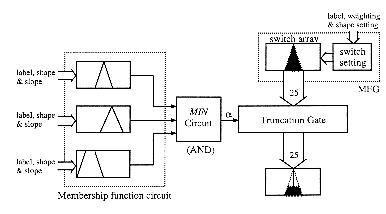
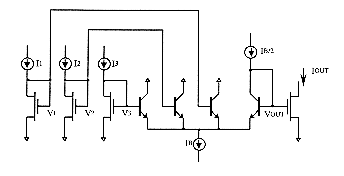
Yamakawa has designed a BiCMOS monolithic rule chip (TG004MC[Yam88],
TG005MC[Hir93]) which architecture is shown on figure 5.3. It is constructed
with about 600 transistors and 800 resistors. The response time of fuzzy
inference is about 1µs (1 Mega- FLIPS). This chip implement one fuzzy
inference including three variables in the antecedent and one variable
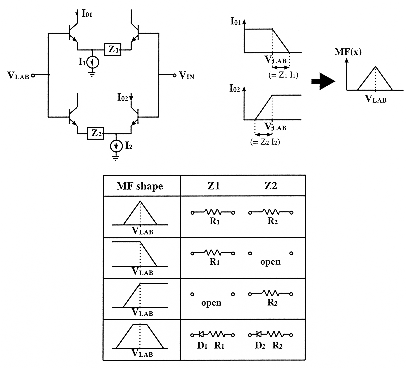
in the consequent. The antecedent part is made of membership function circuits
(fig. 5.4) providing for each variable seven possible fuzzy linguistic
values (one of which is selected according to a voltage label VLAB).
These values can have four possible shapes ![]() assigned by an external binary signal, and the slopes can be changed by
external resistors. A special label "not assigned" corresponding to a constant
high level (+5V) can stand for constant membership functions which value
is 1.
assigned by an external binary signal, and the slopes can be changed by
external resistors. A special label "not assigned" corresponding to a constant
high level (+5V) can stand for constant membership functions which value
is 1.
A truncation circuit is not more than a certain number n of 2-inputs
MIN circuits connected to a n-inputs MAX circuit. A voltage level ![]() as truncation factor is applied to one input of each MIN circuit, and membership
grades of output fuzzy sets are applied to the second inputs. The output
fuzzy sets are sampled in the consequent part by a membership function
generator (MFG) in order to form fuzzy words of 25 elements which can be
processed by the truncation circuit. These words are realised by a switch
array controlled by a switch setting circuit [Gup88],[Yam93], and represent
the consequent membership functions as analog voltages on 25 lines.
as truncation factor is applied to one input of each MIN circuit, and membership
grades of output fuzzy sets are applied to the second inputs. The output
fuzzy sets are sampled in the consequent part by a membership function
generator (MFG) in order to form fuzzy words of 25 elements which can be
processed by the truncation circuit. These words are realised by a switch
array controlled by a switch setting circuit [Gup88],[Yam93], and represent
the consequent membership functions as analog voltages on 25 lines.
![[Zoom]](zoom.gif)
![[Zoom]](zoom.gif)
Yamakawa also designed an analog defuzzifier chip (TB005PL[Yam88], TB010PL[Hir93]) which implements the centre of gravity calculation for 25 values (fig. 5.5). Its architecture consist of an ordinary addition circuit in parallel with a weighted addition circuit, and followed by an analog divider. It is constructed with resistor arrays, OP amplifiers, an analog divider and capacitors in hybrid structure. The response time of defuzzification is about 5µs and is almost determined by that of the divider. The sum calculation is proceeded by a simple network of 25 identical resistors connected to a same node, which produce a current proportional to the desired sum. The weighted addition is proceeded in the same way, but with 25 different resistors: 0,R, R/2, R/3,..., R/24. For an emitter junction of a bipolar transistor, the base-to- emitter voltage is proportional to the logarithm of the emitter current (over the range where the effects of series and shunt resistors and reverse saturation current are negligible). Thus the division of the two currents (proportional to the sum and the weighted sum respectively) is implemented by the subtraction of two base-to-emitter voltages. Finally, the divider is followed by a level shifter with current-voltage conversion [Yam88bis].
Several rule chips can be connected to such a defuzzifier chip which calculate a deterministic value from the maximal membership function. Several defuzzifier chips can also be used to realise systems involving several conditions and several conclusions. The main weak point of such systems is that they generally lead to non-optimal cumbersome implementations.
OMRON has developed the above analog fuzzy chips, as an analog rudimentary fuzzy computer based on these two circuits: the FZ-5000. This last one consists of a multi-boards system, which each board includes four inference chips and one defuzzifier chip. Inference time is about 15µs, including defuzzification. Programming is done using switches and jumper pins, or by a specific software tool (FT-6000) using a personal computer.
![[Zoom]](zoom.gif)
Several functions are very difficult to build in voltage-mode, and it is also true for some basic ones as the algebraic sum. The above described approach needs resistors to achieve additions and to convert voltages into currents. Integrated resistors are unfortunately inaccurate, cumbersome and involve significant parasitic capacitances. The truncation of the consequent and the defuzzification pose an important problem as regards the parallelism of the inference engine (especially when the number and size of output sets is large). This approach implies high-power dissipation and large chip area, and leads to high-costs implementations.
![[Zoom]](zoom.gif)
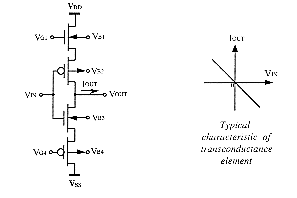
![[Zoom]](zoom.gif)
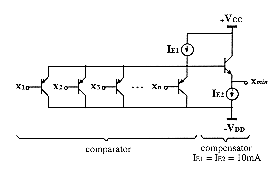
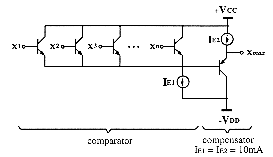
A high-speed bounded difference operation can easily be implemented by use of OTAs. For the circuit represented on fig.5.8, the relationship between the input voltages (VIN1 & VIN2) and the current of the diode satisfies the definition of the bounded difference. As the first OTA supplies a current proportional to the difference of input voltages, the bounded difference is realized for µ1 greater or equal to µ2 when input voltages represent the membership functions µ1 and µ2. It is also realized for µ1 < µ2 since the diode can only pass the unidirectional output current of the OTA. The second OTA finally converts this current into a proportional output voltage (VOUT), in order to obtain a voltage-mode bounded difference characteristic. Its output current is indeed identical to the diode one, and is also proportional to the output voltage which is connected back to an input of the second OTA.
![[Zoom]](zoom.gif)
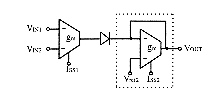
This OTA-based bounded difference operator can be effectively used to
synthesise all other fuzzy function according to the relationships described
in §3.2. The algebraic sum used in these relationships is realised
by simple wire connections before finally converting currents into voltages
with OTAs. The fuzzy complement operation is realized when the positive
input voltage (VIN1) is connected to the high-level (µ1
= 1) in the circuit of fig.5.8 (VOUT is then the complement
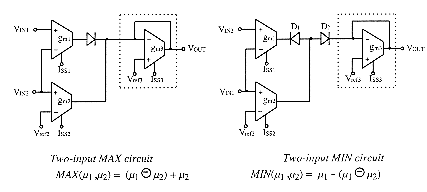
of VIN2). Two-input MAX and MIN operators synthesis are represented
on fig.9. Since µ1 = (µ1![]() µ2) in any case, MIN(µ1 ,µ2)
= µ1
µ2) in any case, MIN(µ1 ,µ2)
= µ1 ![]() (µ1
(µ1![]() µ2) = µ1 - (µ1
µ2) = µ1 - (µ1![]() µ2). The algebraic difference leads to a faster MIN operator
synthesis than two cascaded bounded differences. A current equal to the
negative value -(µ1
µ2). The algebraic difference leads to a faster MIN operator
synthesis than two cascaded bounded differences. A current equal to the
negative value -(µ1![]() µ2) is obtained by permuting the two input voltages (VIN1
as µ1 & VIN2 as µ2) in a common bounded
difference circuit operation which diode (D1) has been connected in reverse
sense. The diode D2 is just useful if the output voltage has to be limited
to positive values.
µ2) is obtained by permuting the two input voltages (VIN1
as µ1 & VIN2 as µ2) in a common bounded
difference circuit operation which diode (D1) has been connected in reverse
sense. The diode D2 is just useful if the output voltage has to be limited
to positive values.
![[Zoom]](zoom.gif)
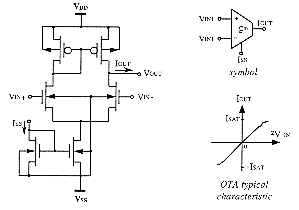
Multiple-input MAX and MIN circuits are also described and analysed in [Inou91], where a fuzzy membership function circuit is also presented. They are made of two-stages OTA structures which provide high-speed signal processing. OTA-based realisations of other fuzzy functions are however often quite complicated and requires more OTAs stages, which radically deteriorates accuracy and speed of processing. Several OTA are actually necessary to synthesise some relationships of §3.2 since many voltage-current or current-voltage conversions are needed before performing bounded differences (which deals with voltages) and algebraic sums (which deals with currents). There is moreover quite difficult to proceed simplifications when these different functions are combined together and the principal optimisation consists of increasing parallelism of OTA stages. This OTA-based approach leads unfortunately rapidly to very big and not so accurate circuits for implementing fuzzy processing of complex inference systems.
![[Zoom]](zoom.gif)
![[Zoom]](zoom.gif)
![[Zoom]](zoom.gif)
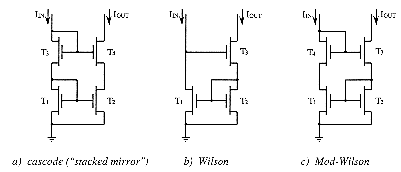
All the above mentioned mirrors can be constructed in standard bipolar technology as well as in MOS one.
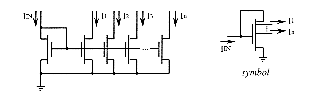
Multiple-output current mirrors can be realized by compact bipolar circuits when using multicollector transistors, whose accuracy is however poorer towards structures with single- collector transistors. Bipolar transistors produce two type of significant errors, due to the base current and to the reverse mode current. The latter causes the saturation of one collector to affect the other collectors, and the circuits should be designed so that no collector in the multiple-output current mirrors may be saturable. These errors do not appear in multiple-output MOS current mirrors since their input-output paths are separated and their drain currents are independent of each other. The design of cascade MOS structures is then much easier than the one of bipolar structures whose stages are interdependent. It is generally preferred, all the more since it is compatible with standard CMOS fabrication processes and efficient design tools.
The mismatch between two identical transistors is however smaller for bipolar than for MOS ones, since it does not depend on the collector current level and since they are affected by a much lesser influence of surface effects. All MOS transistors must work in saturation mode in order to reduce the mismatch effects. Bipolar current mirrors are then more appropriate to work with low voltages and are more precise and fast with low currents (the speed of MOS ones decreases at low currents because of their intrinsic capacitances).
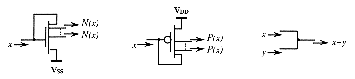
In this way, nine basic fuzzy functions (cf. §3.2: ![]() ) can be easily implemented on monolithic IC's with standard CMOS [Zhij90],[Yam86]
or bipolar technologies [Yam87]. These current-mode basic logic cells exhibit
good linearity which can not be easily achieved in voltage-mode, and lead
to fuzzy integrated systems which are globally smaller than in voltage-mode.
) can be easily implemented on monolithic IC's with standard CMOS [Zhij90],[Yam86]
or bipolar technologies [Yam87]. These current-mode basic logic cells exhibit
good linearity which can not be easily achieved in voltage-mode, and lead
to fuzzy integrated systems which are globally smaller than in voltage-mode.
![[Zoom]](zoom.gif)
A bounded difference circuit can be obtained by the combination of a
current mirror and a diode (fig.5.13). The diode can easily be realized
in the CMOS circuit either by a single FET which gate and drain are connected
together (fig.5.13) or by a current mirror (fig.5.14). The first solution
involves inevitable voltage drops due to the channel resistance and can
influence the normal logic function of the circuits. Nevertheless the diode
can be omitted in cascade connection of such circuits because the input
current mirror of the following stage also achieves its task.
![[Zoom]](zoom.gif)
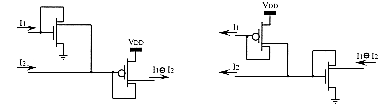
Current mirrors are subdivided into two complementary types whether their transistors are n- or p-channel MOS FET (NPN or PNP in bipolar technology). The directions of input and output currents depend on the type of the respective components (input mirror and output diode in the bounded difference circuit). Thus there are four different configurations of input and output current directions (two of which are shown on fig.5.14 and are suitable for cascade connections). To each configuration corresponds a complementary one which is obtained by substituting p-channel current mirrors to n-channel ones and vice versa. This is convenient for designing circuits using such fuzzy logic units as basic bricks without worrying about specific current directions between neighbouring bricks.
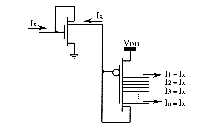
The circuits of fig.5.13 and 5.14 realize the bounded difference operation on two values of membership functions µx & µy represented by the two currents I1 and I2 respectively. They also realize the complement operation on µy (represented by I2) when I1 has the maximum value (that represents a membership grade equal to 1). The bounded product is realized when I1 represents 1 and I2 represents the sum µx + µy. As the bounded difference and the algebraic sum are sufficient to realize all other fuzzy functions (according to the relations described in §3.2), fuzzy circuits can be designed only by specifying connections between bounded difference subcircuits. Multiple-output current mirrors are also required to distribute current to several logic units (fig.5.15). Such basic cells are attractive prospects for developing CAD tools and semicustom IC's (that are arrays of logic cells adaptable to various specifications according to the wire configurations). This leads however to solutions which are generally not optimal as regard to the number of transistors.
Multiple-input MAX and MIN circuits are proposed in [Sas90] which aim at avoiding error accumulation and increasing speed relatively to binary tree realizations based on two-input MIN and MAX subcircuits. The operation of these circuits can be formulated using simultaneous bounded difference equations. A simpler multiple-input MAX circuit is described in [Batu94].
![[Zoom]](zoom.gif)
Three "primitive" operators have been introduced to obtain more elementary basic cells than the bounded difference [Lem93],[Lem93bis],[Lem94]. These operators are defined in the following way :
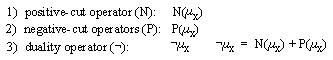
All fuzzy functions can be formulated as an additive combination of these primitive operators since the bounded difference can be expressed in the following way:
![[Zoom]](zoom.gif)
As an example of such a process, the MIN operation can be implemented with two cascade current mirrors (fig.5.17), after having carried out a certain number of simplifications into its mathematical formulation:
![[Zoom]](zoom.gif)
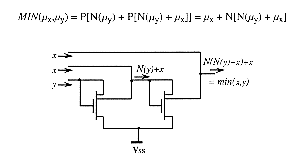
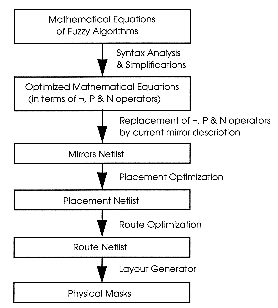
There are various solutions to realize non-linear analog membership function generator in current mode but they are directly influenced by their physical features and often exhibit bad temperature behaviour. Consequently it is quite attractive to design circuitry achieving piecewise-linear membership functions [Kett93],[Yam88-3]. The representation of complicated membership functions can also be subdivided into an appropriate composition of elementary logic subcircuits. The fuzzification of a crisp variable x thought membership functions with triangular shapes can be expressed, for example, in terms of the primitive operators , P and N as follows [Lem94]:
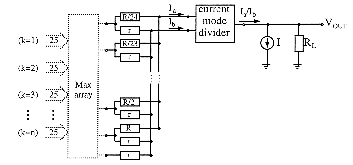
However the required division can be easily and rapidly performed by current-mode normalization circuits [Ishi92]. For the circuit of figure 5.18 there are the following relations:
![[Zoom]](zoom.gif)
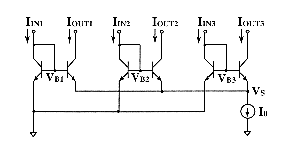
The normalization circuit can directly be extended to more than three inputs. The sum of all output currents is normalized to I0 and so each output current (representing a membership grade) is divided by this sum (sum of all membership grades). There is no more need of dividing the weighted sum of these currents. The weight of each current can be realized in the normalization circuit by the W/L ration of the respective output transistor. Good precision is obtained when such a circuit is implemented by means of bipolar transistors or bipolar operated MOS. When using saturated MOS transistors operating in weak inversion with VS=0 the circuit is very inaccurate and variable with the temperature, due to the large variation of VT0 from device to device.
Yamakawa has searched to eliminate the analog division in a voltage-mode singleton- consequent controller by using grade-controllable membership function circuits (which are obtained by modifying ordinary membership function circuits [Yam89],[Yam93]). These can be tuned in such a way that the sum of all membership grades is equal to the unity (or constant), and that the weighted sum doesn't need any more division. The regulation consists of shifting down and up each membership function characteristic according to the variations of the sum of membership grades, through a negative feedback loop.
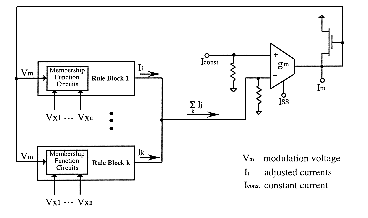
The current-mode rule block with voltage interface (and OTA-based membership
function circuits) described in [Sas92] also includes a normalization locked
loop which abolishes the division operation of the weighted average in
a similar way (fig.5.19). The sum of membership grades (![]() )
is regulated by using its fluctuations as modulation factor (Vm)
of the membership function circuits throughout a negative feedback loop.
This regulation operation is attractive since it is faster than the analog
division in fuzzy hardware implementation. Nevertheless the implementation
of such circuits requires complicated units and connections, and leads
to difficult sizing and testing. The normalization solution described in
§5.4.4 is finally far simpler for current- and mixed-mode circuits.
)
is regulated by using its fluctuations as modulation factor (Vm)
of the membership function circuits throughout a negative feedback loop.
This regulation operation is attractive since it is faster than the analog
division in fuzzy hardware implementation. Nevertheless the implementation
of such circuits requires complicated units and connections, and leads
to difficult sizing and testing. The normalization solution described in
§5.4.4 is finally far simpler for current- and mixed-mode circuits.
![[Zoom]](zoom.gif)
Temporary memory elements have however been proposed to keep signals stable within a sampling period. This allowss to design fuzzy inference engines with pipelined structures and consequently enhanced speed [Zhij90bis]. Such basic memory cells are however not suitable for implementing complicated sequential algebra in the same way that digital circuits do thanks to the use of binary flip-flop and register circuits. An analog value can however be stored in a more lasting way when represented by a voltage, by mean of a capacitor. This last component is the core of sample-and-hold circuits which are basic cells of anolog memory elements.
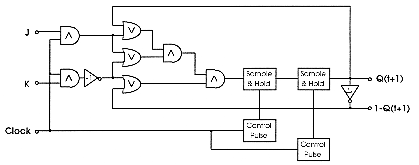
A voltage-mode fuzzy flip-flop has been proposed as an extension form of binary J-K flip- flop [Gup88]. It is based on fuzzy negation, T-norm and S-norm which are respectively restricted to complementation, MIN and MAX operations in order to make easier its hardware implementation. The characteristics of fuzzy flip-flop based on other operations such as algebraic product and sum, bounded product and sum, and drastic product and sum are also reported in [Hir89]. Its structure is described by the following set and reset equations which generate the same state values than a digital J-K flip-flop in the case of boolean input and state values.
The fuzzy flip-flop can be implemented with a combinatorial part synthesising
the above equation, and two sample-and-hold circuits driven by two control
pulse circuits with opposite phases (fig.5.20). Present output Q(t) is
memorized by two sample-and-hold circuits since the information is needed
in the next state.
![[Zoom]](zoom.gif)
Current-mode continuous valued memory elements can also be realized in the same way by using voltage-controlled current sources in both sample-and-hold circuits to store a control voltage representing the sampled current [Balt93]. The capacitor of a sample-and-hold circuit is thus charged according to the control voltage of a first current source. In the "hold mode" (after half a clock cycle), this stored voltage sets the output current through a second current source in the image of the input one.
Storage capacitors are designed according to a trade-off between high speed and small silicon area on one hand, and sufficient accuracy on the other hand (their capacitance should be high relatively to parasitic ones). High accuracy is however difficult to achieve since it is affected by the imprecision of integrated capacitors, the mismatch in couples of current sources, and overall the charge injection in parasitic capacitances. This last source of sampling error is however reduced with the master-slave configuration of the sample-and-hold circuits, since the injected charges are opposite in sign (the first order sampling errors are thus cancelled).
It can actually be attractive to increase the complementarity between digital and analog features and to merge them into a single mixed chip, in order to improve the weak points of both [Fatt93],[Zhij90bis]. A fuzzy knowledge base can be programmed in a digital memory which consists of dedicated locations and stores a variable number of parameters characterizing membership function shapes and inference rules notably. Highly-parallel and non-sequential analog processing is then afforded provided that D/A converters are used. A/D converters can also be used when a digital computation of the centre-of-gravity is desired.
The VLSI Design group of SGS-THOMSON has also undertaken the design of an hybrid controller implemented by means of a mixed analog/digital technology [Pag93bis],[Pag93-3]. It consists of a digital storage and distribution unit followed by an analog inference core. The membership grades are converted into analog values by an internal D/A. This system does not need expensive A/D and D/A converters in comparison with digital controllers. Its high speed should be suitable for very demanding real-time requirements with a limited number of rules.
As the design issued of such a strategy is close to fuzzy algorithms,
it makes easy the test of resulting circuits. Internal currents can however
not be measured without adding supplementary output current mirrors which
increase the circuit size. Gate voltages can be measured but they just
indicate an imprecise estimation of the transistor currents.
![[Zoom]](zoom.gif)
The fusion of neural networks and fuzzy logic do not only concerns their similarities, but also mutual compensations between their different features. Thus neural networks can offer a solution in fuzzy systems to the problems of structure identification (number and size of rules making up a suitable fuzzy partition of the feature space) and parameter identification (number and characteristics of membership functions). They are actually able to replace in some cases the tedious and sometimes hazardous identification scheme by a supervised learning. The knowledge acquisition by self-organizing networks can be used to realize adaptive fuzzy systems, which are quite attractive when linguistic rules cannot be easily derived or when a great deal of rules are required. However there is no guaranty of convergence in the learning scheme. The necessary number of neurons is moreover unpredictable and the acquisition of new knowledge is fairly difficult without beginning a new learning scheme.
There is several manner to combine neural networks and fuzzy logic, which differ according to the authors. The first idea consists of using the high flexibility of neural networks produced by learning, in order to provide automatic design and fine tuning of the membership functions used in fuzzy control. Such an adaptive neuro-fuzzy controller adjusts its performances automatically by accumulating experience in a learning phase. National Semiconductor Corp. has developed the Neufuz embedded system that provides a front-end neural networks suitable for fuzzy logic technology. A first layer performs fuzzification, a second creates the rule base and a third, a single neuron, does rule evaluation and defuzzification. Neural networks involve a great deal of computations and hardware investments which is prohibitive for many real-time applications. So they emulate and optimise in this case a fuzzy logic system rather than implement directly the final application. The National Semiconductor solution includes then the capability to generate assembly code for a strictly fuzzy logic solution. Recently Neuralogix has put on the market the NLX230 fuzzy microcontroller which consists of a VLSI digital fuzzy logic engine based on the min-max method. It includes a neural network implementing a high-speed minimum comparator block connected with 16 parallel fuzzifier on one side and a maximum comparator on the other side. An other approach aims at solving the problems of consequence identification and of defuzzification by using the Takagi-Sugeno's method which lends itself good to implementation framework based on adaptive neural networks [Jan92].
Instead of using neurons to implement some part of fuzzy systems, the structure of approximate reasoning can be applied to neural networks. The aim of this approach is to improve neural network frameworks by bringing some advantages of fuzzy logic. The latter allows an explicit representation of the knowledge and has a logic structure that allows to handle high-order processing easier. In pattern recognition for example, the learning scheme is efficient to acquire a knowledge about reference objects. As for the structure of approximate reasoning rules, it can give information on the knowledge distribution inside the whole network. It is then easier to find out the internal part that cause poor performance by analysis of error according to the rule structure [Tak90bis].
![[Table of Contents]](toc.gif)
![[Top of Document]](top.gif)
This chapter edited by D. Mlynek