![[DBPP]](pictures/asm_color_tiny.gif)





![[Search]](pictures/search_motif.gif)
Next: Chapter Notes
Up: 8 Message Passing Interface
Previous: 8.9 Summary
-
Devise an execution sequence for five processes such that
Program 8.4 yields an incorrect result because of an
out-of-order message.
-
Write an MPI program in which two processes exchange a message of size
N
words a large number of times. Use this program to measure
communication bandwidth as a function of N
on one or more
networked or parallel computers, and hence obtain estimates for
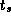 and
and 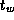 .
.
-
Compare the performance of the program developed in
Exercise 2 with an equivalent CC++
or FM program.
-
Implement a two-dimensional finite difference algorithm using MPI.
Measure performance on one or more parallel computers, and use
performance models to explain your results.
-
Compare the performance of the program developed in
Exercise 4 with an equivalent CC++
, FM, or HPF programs.
Account for any differences.
-
Study the performance of the MPI global operations for different data
sizes and numbers of processes. What can you infer from your results
about the algorithms used to implement these operations?
-
Implement the vector reduction algorithm of Section 11.2
by using MPI point-to-point communication algorithms. Compare the
performance of your implementation with that of MPI_ALLREDUCE
for a range of processor counts and problem sizes. Explain any
differences.
-
Use MPI to implement a two-dimensional array transpose in which an
array of size N
 N
is decomposed over
P
processes ( P
dividing N
), with each process having
N/P
rows before the transpose and N/P
columns after.
Compare its performance with that predicted by the performance models
presented in Chapter 3.
N
is decomposed over
P
processes ( P
dividing N
), with each process having
N/P
rows before the transpose and N/P
columns after.
Compare its performance with that predicted by the performance models
presented in Chapter 3.
-
Use MPI to implement a three-dimensional array transpose in which an
array of size N
 N
N
 N
is decomposed over
N
is decomposed over
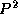 processes. Each processor has
(N/P)
processes. Each processor has
(N/P)
 (N/P)
x/y
columns before the transpose, the same number of x/z
columns
after the first transpose, and the same number of y/z
columns
after the second transpose. Use an algorithm similar to that
developed in Exercise 8 as a building block.
(N/P)
x/y
columns before the transpose, the same number of x/z
columns
after the first transpose, and the same number of y/z
columns
after the second transpose. Use an algorithm similar to that
developed in Exercise 8 as a building block.
-
Construct an MPI implementation of the parallel parameter study
algorithm described in Section 1.4.4. Use a single
manager process to both allocate tasks and collect results. Represent
tasks by integers and results by real numbers, and have each worker
perform a random amount of computation per task.
-
Study the performance of the program developed in
Exercise 10 for a variety of processor counts and problem
costs. At what point does the central manager become a bottleneck?
-
Modify the program developed in Exercise 10 to use a
decentralized scheduling structure. Design and carry out experiments
to determine when this code is more efficient.
-
Construct an MPI implementation of the parallel/transpose and
parallel/pipeline convolution algorithms of
Section 4.4, using intercommunicators to structure the
program. Compare the performance of the two algorithms, and account
for any differences.
-
Develop a variant of Program 8.8 that implements the
nine-point finite difference stencil of Figure 2.22.
-
Complete Program 8.6, adding support for an accumulate
operation and incorporating dummy implementations of routines such as
identify_next_task.
-
Use MPI to implement a hypercube communication template (see
Chapter 11). Use this template to implement simple
reduction, vector reduction, and broadcast algorithms.
![[DBPP]](pictures/asm_color_tiny.gif)





![[Search]](pictures/search_motif.gif)
Next: Chapter Notes
Up: 8 Message Passing Interface
Previous: 8.9 Summary
© Copyright 1995 by Ian Foster
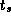 and
and 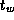 .
.
 N
is decomposed over
P
processes ( P
dividing N
), with each process having
N/P
rows before the transpose and N/P
columns after.
Compare its performance with that predicted by the performance models
presented in Chapter 3.
N
is decomposed over
P
processes ( P
dividing N
), with each process having
N/P
rows before the transpose and N/P
columns after.
Compare its performance with that predicted by the performance models
presented in Chapter 3.
 N
N
 N
is decomposed over
N
is decomposed over
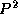 processes. Each processor has
(N/P)
processes. Each processor has
(N/P)
 (N/P)
x/y
columns before the transpose, the same number of x/z
columns
after the first transpose, and the same number of y/z
columns
after the second transpose. Use an algorithm similar to that
developed in Exercise 8 as a building block.
(N/P)
x/y
columns before the transpose, the same number of x/z
columns
after the first transpose, and the same number of y/z
columns
after the second transpose. Use an algorithm similar to that
developed in Exercise 8 as a building block.
![[DBPP]](pictures/asm_color_tiny.gif)





![[Search]](pictures/search_motif.gif)